aとkの一般的な関係


において、k=1とおくと、
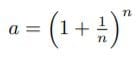
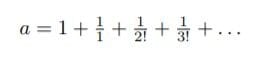
となる。このときの底aをオイラーは文字e(注1)で表わすことにした。すなわち、
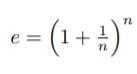

である。
上の形はヤコブ・ベルヌーイの「連続複利の元利合計」、下の形はヨハン・ベルヌーイの「対数が1となる数」(注2)が背景にあるだろう。
オイラーは計算して、e = 2.71828 18284 59045 23536 028の値を出している。
注1
文字eはEulerのeというよりも、exponential(指数)のeだろう。オイラーはネイピア数とは言っていない。自然対数もしくは双曲線対数の底を表わしていると言っている。
注2
志賀浩二『数の大航海』に次のようにある。


において、k=1とおくと、
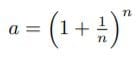
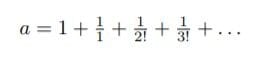
となる。このときの底aをオイラーは文字e(注1)で表わすことにした。すなわち、
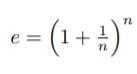

である。
上の形はヤコブ・ベルヌーイの「連続複利の元利合計」、下の形はヨハン・ベルヌーイの「対数が1となる数」(注2)が背景にあるだろう。
オイラーは計算して、e = 2.71828 18284 59045 23536 028の値を出している。
注1
文字eはEulerのeというよりも、exponential(指数)のeだろう。オイラーはネイピア数とは言っていない。自然対数もしくは双曲線対数の底を表わしていると言っている。
注2
志賀浩二『数の大航海』に次のようにある。
ヨハン・ベルヌーイは、1696年12月にライプニッツに宛てた手紙の中で、対数を積分する過程で、対数が1となる数をcと表わし、cは
と表わされ数であると伝えている。










