正多面体の双対

5つの正多面体の頂点、辺、面の数をまとめると次のようになる。
　　　　　 　 頂点数　　　辺数　　面数
正八面体　　　　6　　　　12　　　　8
正六面体　　　　8　　　　12　　　　6
正二十面体　　 12　　　　30　 　　 20
正十二面体　 　20　　　　30　 　　 12
正四面体　　　　4　　　　 6　　　　 4　　

正八面体と正六面体（立方体）は辺の数は共通で、頂点と面の数が入れ替わっている。正二十面体と正十二面体も同じ関係にある。正四面体は頂点と面の数が等しく、内部で入れ替われる。
このような関係（双対）があることは知っていたが、この関係を最初に発見したのはケプラーとは知らなかった。（『世界で二番目に美しい数式』参照。）
『宇宙の調和』（岸本良彦訳）でケプラーは次のように述べていた。
（引用はじめ）
これらの図形の中では、相異なる部類で結びついた、いわば2組の夫婦が目に付く〔つまり双対的である〕。男性は基本図形に入る立方体と正12面体、女性は副次的な図形の正8面体と正20面体である。それにいわばひとりの独身者ないし男女である正四面体が加わる。
（引用おわり）
基本図形とは1つの頂点に3つの面が集まるもの、副次的な図形とは面の数が4または5のものをいう。また、頂点（立体角）が男性の、面が女性の象徴で、面の数より頂点（立体角）の数の多い正多面体は男性、頂点（立体角）より面の数の多い正多面体は女性である。

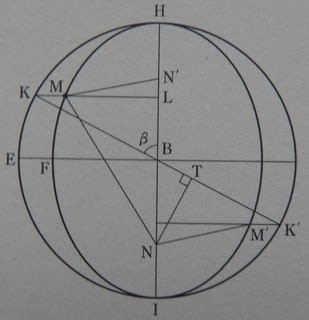
これはケプラーが正多面体の双対性を示すために描いた図である。
立方体の面と正八面体の頂点が対応していることがわかる。また、正八面体の辺と立方体の辺が直交関係にあり、1対1に対応していて、同じ数であることもわかる。同じことが、正二十面体と正十二面体の双対にも正四面体の双対にもみることができる。

付録
（まちがい発見）
『世界で二番目に美しい数式』第6章ケプラーの多面体宇宙、78ページに次のようにある。
「ケプラーはこの裏返しの関係が図形的に解釈できることに気づいた。たとえば、正多面体の1つとして立方体を考えよう。その各面の中心に新しい頂点を置くと、その8個の点は1つの正八面体の頂点の配置になっている。この新しい多面体はもとの多面体の双対（そうつい）とよばれる。」
「8個の点」は「6個の点」の間違いである。訳者？　原典『Euler’s Gem』？

危機一髪

今日も暖かい一日だった。昨日の残りの枇杷の枝と葉を束ねた。２束になった。その後、クロガネモチを切った。道路に面しているので、切り倒すのではなく、上の方から、輪切りにして、徐々に短くしていった。脚立を使った。危険な作業だったろう。次にナンキンハゼの枝を切った。これにも脚立を使った。垂直の枝を切った後、落ちていく枝を見ていたが、このとき、右手に持っていたチェーンソーが、左の大腿部に絡んだ。チェーンソーを離したが、作業ズボンが十字の形に10センチほど破れた。太ももに接触した感触があった。のぞいてみると、出血はなく、1ミリほどの太さの線が5センチほど見えた。血はにじんでいた。痛くはないが、少しひりひりする。バンドエイドを貼るまでもなかったが、危なかった。
明日は今日切った枝の後始末である。安全第一にやろうと思う。

枇杷の木は残った

昨年の予定では枇杷の木は全部切り倒してすっきりさせるつもりだった。今日、久しぶりにチェーンソーを使って、枇杷の木を切った。玄関先の、高さ４メートルほどの細い幹を5本。そのうち、３本分は束ねた。大きな束が２つ。残りは明日だが、玄関先がすっきりした。後２か所あるが、今日の分だけで、ずいぶんと整理された。南側の枇杷は切り倒す必要はなく、剪定する程度でいいかもしれない。東側の枇杷は本家の枇杷だが、これも剪定するだけにして残そうと思う。

オイラーの多面体公式

『世界で二番目に美しい数式』（デビット･S.リッチェソン著、根上生也訳、岩波書店、2014年）を借りてきた。世界で2番目に美しい数式とはオイラーの多面体公式であった（1番目はいわゆる「オイラーの公式」である）。頂点、辺、面の個数をそれぞれV、E、Fとすると、
V－E＋F＝2
という関係が成り立つというもの。中学や高校の幾何にも出ている式である。「誰もが見逃していた」が、やっと1750年にオイラーによって発見された。
正多面体が5つしかないこともこの多面体公式から導けるようである。
公式が発見されるまでの歴史、公式を出発点に誕生したトポロジーの考え方や応用例が展開されるという。後半は難しそうだが、がんばって読んでみよう。

アオキの実

木の股の近くで実がなっているのが多いが、これはかなり離れて実をつけている。花の茎が長かったのだろう。アーチの長さは１０センチほど。

キツネの知恵

「すっぱい葡萄」（キツネとブドウ）の話は、「負け惜しみ」や「合理化」と否定的にみるのが一般的だが、これは偏っている。むしろ積極的に羨望を拒否する健全な保守の知恵と捉えるべきである。このような見方が『悪の引用句辞典』（鹿島茂著、中公新書、2013）に提示されている。
（引用はじめ）
手の届かないところにあるブドウを見たキツネは、「あれはまだ青すぎる。下賤のやつらの食うものだ」と言って断念したが、これに対して、ラ・フォンテーヌ先生はこう論評している。

キツネは愚痴をこぼすよりもましなことをしたのではあるまいか。

『失われた時を求めて』の大伯母（注）は、キツネの知恵に倣おうとするフランス人の一典型なのである。
（引用おわり）
永遠に自分のままでいられる知恵。「分相応」、「矩を踰えず」の積極的な意味。西部邁もキツネの知恵に倣おうとしていたのではないかと思う。

（注）
「大伯母は、どんな小さなことでも自分にない強みが他人にあると思うと、かならずそれは強みではなく弱みなのだと自分に納得させ、その人たちを羨ましく思うのが嫌さに、逆に彼らを憐れむのだった。」

赤実と黄実の千両

西側にある千両の実はほとんどなくなっているが、東側にある千両の実は残っている。この冬はヒヨドリとメジロがいつもいたという印象である。東側も実が食べられてもおかしくないはずだが残っている。こういうことだったろう。東側のはミカンの木の下にある。鳥にしてみれば、わざわざ千両の実を食べなくとも、ミカンの実で十分だった。赤実の千両も黄実の千両も、切って使った分以外はそのまま残っている。ただ、自然に落ちはじめる時期にきている。

これは自然のままではなく、少し離れたところにある黄実の千両の枝を切って、赤実の千両に置いたものである。こんどはこの赤実の千両の枝を切って、玄関に赤実と黄実の千両を飾るという運びである。

楕円軌道の証明4

離心円上の任意の点Kから長軸HIに垂線KLを下ろすとき、この垂線は点Mにおいて同じ比1:√(1－e²)に分割される。これはアポロニウスの楕円に対応させた楕円軌道の証明である。これは『新天文学』（1609年）の証明で、「楕円軌道の証明1」で示した。ケプラーはその後、太陽を楕円の焦点に位置づけた。そして楕円の性質「2つの焦点から楕円上の任意の点に引かれた線分の和は、つねに長径に等しい」に対応させる証明も可能になった。こちらは「楕円軌道の証明3」でみている。
下図（「ケプラーの第1法則（楕円軌道）の証明」、山本義隆『世界の見方の転換』3）で離心円の直径をKK'（長径）とする。K、K'から長軸線に下した垂線が楕円と交わる点をM、M'とすると、

NM＋N'M=NM＋NM'=KT＋TK'=KK'

であることをみた。これは『新天文学』にはなかった証明である。しかし、これぱ幾何学的なものだったので、ここでは代数的にみておこう。
離心円の半径を1、離心率をeとする。また、NとN'は焦点である。NM＋N'M＝2を証明する。

△MNLに着目して、
NM²＝NL²＋ML²
ここで
NL＝e＋cosβ
ML＝√(1－e²)･sinβ　　（注）
より、
NM²
＝(e＋cosβ) ²＋(1－e²)sin²β
＝e²＋2ecosβ＋cos²β＋sin²β－e²sin²β
ここでcos²β＋sin²β＝1だから、
＝1＋2ecosβ＋e²(1－sin²β)
＝1＋2ecosβ＋e²cos²β
＝(1＋ecosβ)²
したがって、
NM＝1＋ecosβ

同じように、△MN'Lに着目して、
N'M²＝N'L²＋ML²
ここで
N'L＝e－cosβ
ML＝√(1－e²)･sinβ
より、
N'M²
＝(e－cosβ) ²＋(1－e²)sin²β
＝e²＋2ecosβ＋cos²β＋sin²β－e²sin²β
＝1－2ecosβ＋e²(1－sin²β)
＝1－2ecosβ＋e²cos²β
＝(1－ecosβ)²
したがって、
N'M＝1－ecosβ

したがって、
NM＋N'M＝(1＋ecosβ)＋(1－ecosβ)＝2
点Mは2点NとN'を焦点とする楕円上の点である。

図の長径HI＝KK'と対応させておこう。

NM＝1＋ecosβ
＝KB＋BT＝KT
また、N'M＝1－ecosβ
＝K'B－ecosβ
＝K'B－BT＝K'T
したがって、
NM＋N'M＝KT＋TK'=KK'

（注）「楕円軌道の証明1」参照

メスのモズが来た

首にカメラをぶら下げて庭にいた。とくにあてはなかった。ユスラウメに止まっている鳥に気づいた。スズメのようだが、色遣いが違った。名前が出てこない。尾を振るのが見えた。すぐに飛び立った。目で追っていくと、枝を切り落としたハナモモの木に止まった。初めて見る鳥である。鳥はしばらく止まっていた。ありがたい。４枚撮れたが、２枚は姿が欠けていた。そのうち、飛び立って、隣の庭に行ってしまった。カメラの画像をみるが、やはり知らない鳥である。
調べていると、メスのモズのように思えてきた。調べるまでモズとはまったく思わなかった。１月下旬に初めてモズを確認したとき、目の周りの黒い帯（過眼線）が特徴だと思っていた。これはオスの特徴で、メスの過眼線は褐色、腹面には波状の横縞が入るとある。間違いないと思う。メスのモズをはじめて見た。

ケプラーの｢あれ｣と｢これ｣

『新天文学』の出版は1609年だが、1605年にはほぼ完成していたという（『新天文学』訳者岸本良彦解説参照）。1604年の『光学』には、楕円の焦点や２定点をむすぶ線分の和が一定の点の軌跡という楕円の定義がある。この時点で楕円軌道と焦点は結びつく可能性はあるが、実現していない。
『新天文学』（1609年）には楕円軌道はあったが焦点はない。『光学』には焦点や２定点をむすぶ線分の和が一定の点の軌跡という楕円の定義はあったが、楕円軌道はない。『新天文学』では楕円軌道の発見だけがあった。『光学』では楕円の「焦点」の導入だけがあった。この2つは別々の出来事で、2つの関連についてケプラーはまだ気づいていなかったのではないだろうか。
楕円軌道と焦点が結びつくのは『宇宙の調和』（1619年）においてである。

惑星軌道は楕円である。そして運動の源泉である太陽はこの楕円の一方の焦点にある。