4 i2=j2=k2=ijk=-1
ij=-ji=kからどのようにして基本公式
i2=j2=k2=ijk=-1
が出現したのだろうか。
次の図を出発としよう。

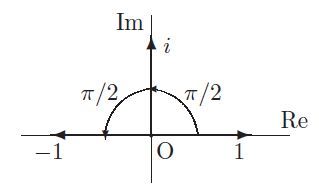
ここは3次元で3つの軸(実軸1、虚軸i,j)が示されている。
1-i-i2は、垂直の平面を回転して-1に達する。
1-j-j2は、水平の平面を回転して-1に達する。
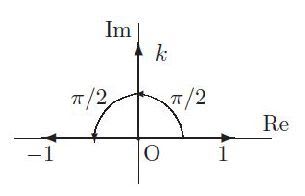
ここに虚軸k(第4の元k)が付け加わる。

ここでkはij=-jiによって生成すると仮定されたものである。図の青の矢印はij=k、赤の矢印はji=-kである。図は直交関係にある4つの軸(実軸1、虚軸i,j,k)を3次元で表示するため角度の関係は保存されていない。ハミルトンは、ここで1-k-k2の回転の終点を洞察したのである。

ij=-ji=kである。また、i2=-1,j2=-1である。
1
ij=-ji=kよりijk=k2が導かれる。
ij・(-ji)
=ijk
=(ij)k
=k2
2
k2とi2=-1,j2=-1の関連が洞察される。
k2
=ij・(-ji)
=ijij
=-i(ij)j
=-iijj
=-i2j2
ここで、i2=-1,j2=-1より、
k2
=-(-1)(-1)
=-1
ijk=k2がi2とj2と同時に-1に達したとき、基本公式が誕生した。1-i-i2は垂直の平面を回転して、1-j-j2は水平の平面を回転して-1に達する。ijk=k2は斜面(垂直のようにもみえ、水平のようにもみえる平面)を回転して-1に達する。
3
すべての「虚」が「実」に変換される。
i2=j2=k2=ijk=-1
注
図はウィキペディアの記事(4元数)から拝借した。

は
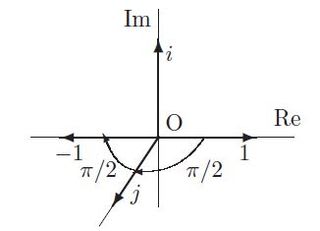
と虚軸jの向きが違うが、同じ場面である。

は

と同じ場面である。見直せば、4分図(下)は8分図(上)の実軸と虚軸kが重なったものである。4分図では1-k-k2の回転は見えなかった。8分図では2つ軸が分離しているので、1-k-k2の回転をみることができる。これが改良点である。
ウィキペディアの図は矢野忠先生に教えていただいた。感謝いたします。
ij=-ji=kからどのようにして基本公式
i2=j2=k2=ijk=-1
が出現したのだろうか。
次の図を出発としよう。

ここは3次元で3つの軸(実軸1、虚軸i,j)が示されている。
1-i-i2は、垂直の平面を回転して-1に達する。
1-j-j2は、水平の平面を回転して-1に達する。
ここに虚軸k(第4の元k)が付け加わる。

ここでkはij=-jiによって生成すると仮定されたものである。図の青の矢印はij=k、赤の矢印はji=-kである。図は直交関係にある4つの軸(実軸1、虚軸i,j,k)を3次元で表示するため角度の関係は保存されていない。ハミルトンは、ここで1-k-k2の回転の終点を洞察したのである。

ij=-ji=kである。また、i2=-1,j2=-1である。
1
ij=-ji=kよりijk=k2が導かれる。
ij・(-ji)
=ijk
=(ij)k
=k2
2
k2とi2=-1,j2=-1の関連が洞察される。
k2
=ij・(-ji)
=ijij
=-i(ij)j
=-iijj
=-i2j2
ここで、i2=-1,j2=-1より、
k2
=-(-1)(-1)
=-1
ijk=k2がi2とj2と同時に-1に達したとき、基本公式が誕生した。1-i-i2は垂直の平面を回転して、1-j-j2は水平の平面を回転して-1に達する。ijk=k2は斜面(垂直のようにもみえ、水平のようにもみえる平面)を回転して-1に達する。
3
すべての「虚」が「実」に変換される。
i2=j2=k2=ijk=-1
注
図はウィキペディアの記事(4元数)から拝借した。

は

と虚軸jの向きが違うが、同じ場面である。

は

と同じ場面である。見直せば、4分図(下)は8分図(上)の実軸と虚軸kが重なったものである。4分図では1-k-k2の回転は見えなかった。8分図では2つ軸が分離しているので、1-k-k2の回転をみることができる。これが改良点である。
ウィキペディアの図は矢野忠先生に教えていただいた。感謝いたします。