「負の数」×「負の数」はなぜ正の数になるのか？

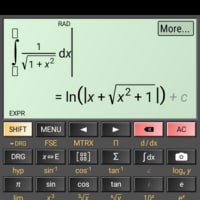
　中学に入りたてに正の数・負の数を教わります。数直線に整数値をプロットするところはまでは皆さん良く理解できることでしょう。
少し進んで整数の加減乗除を学びます。加減算まではなんとか数直線を利用してイメージさせることはできるでしょう。
しかし、乗算となると「なんでー？？？」ということになります。

　私の場合には
　「正の数」×「正の数」⇒「正の数」　・・・①
　「正の数」×「負の数」⇒「負の数」　・・・②
　「負の数」×「正の数」⇒「負の数」　・・・③
　「負の数」×「負の数」⇒「正の数」　・・・④
といったことを掛け算の九九みたいに覚えさせられました。

　分からないことに対して「何で―？」と疑問を持つことは大切なことなんです。しかし、これらに対しては明確な答えを得られるものと得られないものがあります。
　「負の数」×「負の数」⇒「正の数」というのは定義（決めごと）なのです。だから覚えるしかないと言ったら身も蓋もありませんが・・・。
ただ、このように決めた方が便利というか都合が良いのです。このことは後に他の分野を学ぶと色々なところで実感できると思います。
それに①~④までを眺めてみると「正の数」と「負の数」で２個ずつでちょうどバランス取れています。もし④を「負の数」決めてしまうと３対１とバランスに欠けてしまいます。アンバランスなものよりバランスがとれていた方が見た目にも麗しいし安定感もありますよね。人はそういうところに魅かれるのではないでしょうか。ですから数学にもそういったことがあるのではないかと思うのです。

　さて、数学って何でも明確な答えがあるものだと思い込んでいらっしゃる方もおられると思います。「負の数」×「負の数」⇒「正の数」の意味がさっぱり分からない。だから数学は訳が分からない難しいものだと思い込んで数学に興味を失ってしまうといった図式に陥らないようにしてもらいたいと切に願います。

　数学においては前提が正しいかどうかは問題にされないのです。その前提から出発して論理的に導かれたものは全て正しいということになります。
　しかし、科学においては、前提から出発して論理的に導かれたものが実験事実と異なれば、その前提が正しくないことになります。
数学は頭の中だけの出来事であって極論すれば何だって空想が可能なのです。例えそれが現実的なことでなくても。現実の世界で起こっていることに当てはめて初めて科学となり得るのです。

　現実離れしている自由数学を勉強して何になるのだという声が聞こえてきそうです。でも自由に発想できる数学だからこそ広がる世界もあるのです。何に使えるか分からないものの成果が現実世界を表現できるものに発展する可能性はいくらでもあります。

　数学を勉強するには紙と鉛筆（表現が古臭すぎる？）と頭脳があれば十分です。それだけで森羅万象を論ずることができます。面白いと思いませんか！？