「感想:『天地明察』」の記事で取り上げた算術の問題が解決したので改めて記事を書く。解決はcobozeさん、Fakirさんの多大なご協力があってが故のことである(というか、私自身は確認するだけだった orz)。改めて両氏に感謝の意を記しておきたい。
冲方丁の小説『天地明察』の20ページ前後に記された問題は以下の通り。
『今、図のごとく釣(高さ)が9寸、股(底辺)が12寸の勾股弦(直角三角形)があり、内部に直径が等しい円を二つ入れる。円の直径はいくらか。』

答えは30/7寸と書かれていた。また、その答えを導いた計算方法も書かれてはいたが、問題を見たときに考えた解き方とその式とはかけ離れていた。
図をまず以下のものとする。青字は線分の長さを示す。
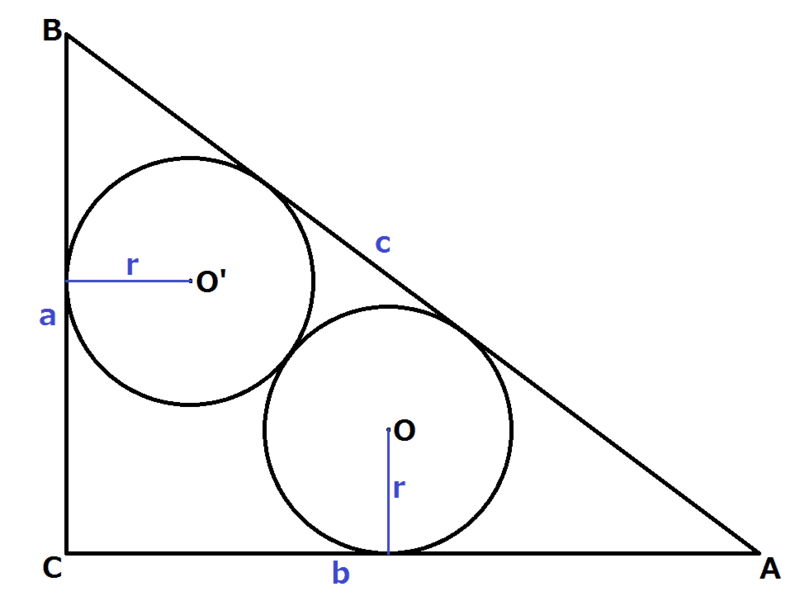
計算方法は、{ 2ab / ( a + b + c ) } ・ { c / ( a + b ) }というものだった。
■面積を分割して解く方法
cobozeさんがOKWaveの質問の中から見つけてくれた方法。質問は直角三角形ではないが、解法は変わらない。

△ABCの面積は ab / 2 = 54
△ABC = △AOC + △COO' + △BCO' + □ABOO' ・・・①
△AOC = br / 2 = 6r
△BCO' = ar / 2 = 9/2・r
□ABOO' = ( 2r + c ) * r / 2 = r^2 + 15/2・r
△COO'はOO'を底辺とすると、△ABCで底辺をABとした場合の高さから r を引いたものが高さとなる。△ABCで底辺をABとした場合の高さを h とすると、ch / 2 が△ABCの面積となる。15/2・h = 54 なので、h =36 / 5 。よって、△COO'の高さは、36 / 5 - r となる。
△COO' = 2r( 36/5 - r ) / 2 =36/5・r - r^2
①に代入すると、
54 = 6r + 9/2・r + r^2 + 15/2・r + 36/5・r - r^2
126/5・r = 54
r = 270/126 = 15/7
求めたのは直径なので、これを2倍した 30/7 で明察となる。
しかし、解法の式とは合致しない。
■相似から解く方法
Fakirさんが示してくれた△ABCと△OO'Zの比から解く方法。

OとO'からACとBCに垂線を下ろす。OからBCへの垂線とO'からACへの垂線の交点をZとする。△OO'Zは△ABCと相似である。OZを x 、O'Zを y とする。また、OからACへの垂線とACとの交点をPとし、線分APの長さを p 、O'からBCへの垂線とBCとの交点をQとし、線分BQの長さを q とする。
辺AC = p + x + r = 12
辺BC = q + y + r = 9
辺AB = p + 2r + q = 15 ・・・①
p = 12 - x - r 、q = 9 - y - r として①に代入すると、
( 12 - x - r ) + 2r + ( 9 - y - r ) = 15
x + y =6
相似から、x :y = 9 :12 なので、y = 12/9・x となる。代入すると、
x + 12/9・x = 6
21/9・x = 6
x = 54/21 = 18/7
これより、y =24/7 となる。
三平方の定理より、
x^2 + y^2 = (2r)^2
(18/7)^2 + (24/7)^2 = 4r^2
r^2 = ( 324 + 576 ) / 49 / 4 = 225 / 49 = ( 15 / 7 )^2
r は正なので、r = 15/7 となる。直径は2倍なので30/7で明察。
■辺の長さから解く方法
これは相似から解く方法をシンプルにしたもので、Fakirさんが提示してくれたもの。

図も相似のものと同じ。x と y を相似から r と a 、b を使って表す。
x :2r = b :c
x = 2r・b/c
y :2r = a :c
y = 2r・a/c
これにより、
辺AC = p + 2r・b/c + r = 12
辺BC = q + 2r・a/c + r = 9
p = 12 - 13/5・r
q = 9 - 11/5・r
辺AB = p + 2r + q = 15 に代入して、
12 - 13/5・r + 2r + 9 - 11/5・r = 15
14/5・r = 6
r =30/14 = 15/7
■三角形の内接円の公式から迫る

図のように内接する円が1つの場合、
△ABC = △ABO + △BCO + △ACO
ab / 2 = cr / 2 + ar / 2 + br / 2
ab = ( a+ b + c ) r
r = ab / ( a+ b + c )
これは、解法の式 { 2ab / ( a + b + c ) } ・ { c / ( a + b ) } と全く同じである(直径なので2倍されている)。
ここでcobozeさんの鋭い洞察があった。

この黄色い部分を合わすと、

片方の円だけを内接する三角形と同じものとなる。
△ABCに一つだけ内接する円を想定し、その半径を R とする。
R :r =c :c - 2r
r = ( c - 2r ) / c ・R
cr = cR - 2rR
( c + 2R ) r = cR
r = cR / ( c + 2R )
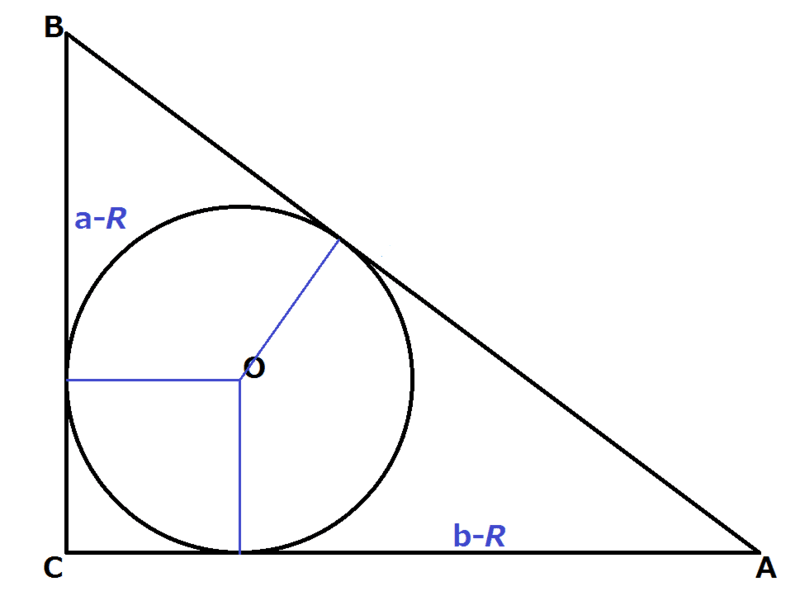
上図より、
c = a - R + b - R = a + b - 2R
これを代入して、
r = cR / ( a + b - 2R + 2R )
r = R ・ c / ( a + b )
R = ab / ( a+ b + c ) より、
r = { ab / ( a+ b + c ) }・{ c / ( a + b) }
2r = { 2ab / ( a+ b + c ) }・{ c / ( a + b) }
となり、式の謎が解けた。
答えは一つでも、その解き方は多種多様。それが数学の面白さでもある。今回の問題では考えるのは人任せになってしまったがそれでも楽しめた(笑)。数学的ひらめきと論理の積み重ねで答えに迫っていく喜びは悩んでこそ得られるものだろう。
小説の本筋ではなかったせいか、中学レベルの問題(?)だったせいか、小説内で詳しい説明がなかったことが結果として楽しみの種となった。そこまで著者の仕掛けだとは考えにくいが、いい問題だったのは確かだ。
コメント用に図を追加


図9

冲方丁の小説『天地明察』の20ページ前後に記された問題は以下の通り。
『今、図のごとく釣(高さ)が9寸、股(底辺)が12寸の勾股弦(直角三角形)があり、内部に直径が等しい円を二つ入れる。円の直径はいくらか。』

答えは30/7寸と書かれていた。また、その答えを導いた計算方法も書かれてはいたが、問題を見たときに考えた解き方とその式とはかけ離れていた。
図をまず以下のものとする。青字は線分の長さを示す。

計算方法は、{ 2ab / ( a + b + c ) } ・ { c / ( a + b ) }というものだった。
■面積を分割して解く方法
cobozeさんがOKWaveの質問の中から見つけてくれた方法。質問は直角三角形ではないが、解法は変わらない。

△ABCの面積は ab / 2 = 54
△ABC = △AOC + △COO' + △BCO' + □ABOO' ・・・①
△AOC = br / 2 = 6r
△BCO' = ar / 2 = 9/2・r
□ABOO' = ( 2r + c ) * r / 2 = r^2 + 15/2・r
△COO'はOO'を底辺とすると、△ABCで底辺をABとした場合の高さから r を引いたものが高さとなる。△ABCで底辺をABとした場合の高さを h とすると、ch / 2 が△ABCの面積となる。15/2・h = 54 なので、h =36 / 5 。よって、△COO'の高さは、36 / 5 - r となる。
△COO' = 2r( 36/5 - r ) / 2 =36/5・r - r^2
①に代入すると、
54 = 6r + 9/2・r + r^2 + 15/2・r + 36/5・r - r^2
126/5・r = 54
r = 270/126 = 15/7
求めたのは直径なので、これを2倍した 30/7 で明察となる。
しかし、解法の式とは合致しない。
■相似から解く方法
Fakirさんが示してくれた△ABCと△OO'Zの比から解く方法。

OとO'からACとBCに垂線を下ろす。OからBCへの垂線とO'からACへの垂線の交点をZとする。△OO'Zは△ABCと相似である。OZを x 、O'Zを y とする。また、OからACへの垂線とACとの交点をPとし、線分APの長さを p 、O'からBCへの垂線とBCとの交点をQとし、線分BQの長さを q とする。
辺AC = p + x + r = 12
辺BC = q + y + r = 9
辺AB = p + 2r + q = 15 ・・・①
p = 12 - x - r 、q = 9 - y - r として①に代入すると、
( 12 - x - r ) + 2r + ( 9 - y - r ) = 15
x + y =6
相似から、x :y = 9 :12 なので、y = 12/9・x となる。代入すると、
x + 12/9・x = 6
21/9・x = 6
x = 54/21 = 18/7
これより、y =24/7 となる。
三平方の定理より、
x^2 + y^2 = (2r)^2
(18/7)^2 + (24/7)^2 = 4r^2
r^2 = ( 324 + 576 ) / 49 / 4 = 225 / 49 = ( 15 / 7 )^2
r は正なので、r = 15/7 となる。直径は2倍なので30/7で明察。
■辺の長さから解く方法
これは相似から解く方法をシンプルにしたもので、Fakirさんが提示してくれたもの。

図も相似のものと同じ。x と y を相似から r と a 、b を使って表す。
x :2r = b :c
x = 2r・b/c
y :2r = a :c
y = 2r・a/c
これにより、
辺AC = p + 2r・b/c + r = 12
辺BC = q + 2r・a/c + r = 9
p = 12 - 13/5・r
q = 9 - 11/5・r
辺AB = p + 2r + q = 15 に代入して、
12 - 13/5・r + 2r + 9 - 11/5・r = 15
14/5・r = 6
r =30/14 = 15/7
■三角形の内接円の公式から迫る

図のように内接する円が1つの場合、
△ABC = △ABO + △BCO + △ACO
ab / 2 = cr / 2 + ar / 2 + br / 2
ab = ( a+ b + c ) r
r = ab / ( a+ b + c )
これは、解法の式 { 2ab / ( a + b + c ) } ・ { c / ( a + b ) } と全く同じである(直径なので2倍されている)。
ここでcobozeさんの鋭い洞察があった。

この黄色い部分を合わすと、

片方の円だけを内接する三角形と同じものとなる。
△ABCに一つだけ内接する円を想定し、その半径を R とする。
R :r =c :c - 2r
r = ( c - 2r ) / c ・R
cr = cR - 2rR
( c + 2R ) r = cR
r = cR / ( c + 2R )

上図より、
c = a - R + b - R = a + b - 2R
これを代入して、
r = cR / ( a + b - 2R + 2R )
r = R ・ c / ( a + b )
R = ab / ( a+ b + c ) より、
r = { ab / ( a+ b + c ) }・{ c / ( a + b) }
2r = { 2ab / ( a+ b + c ) }・{ c / ( a + b) }
となり、式の謎が解けた。
答えは一つでも、その解き方は多種多様。それが数学の面白さでもある。今回の問題では考えるのは人任せになってしまったがそれでも楽しめた(笑)。数学的ひらめきと論理の積み重ねで答えに迫っていく喜びは悩んでこそ得られるものだろう。
小説の本筋ではなかったせいか、中学レベルの問題(?)だったせいか、小説内で詳しい説明がなかったことが結果として楽しみの種となった。そこまで著者の仕掛けだとは考えにくいが、いい問題だったのは確かだ。
コメント用に図を追加


図9










