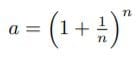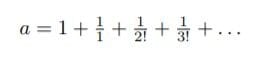雨を待つ
2020-10-16 | 日記
物置に使っている家屋(平屋)の雨樋が、2、3年前からだめになっている。中央付近の留め金が錆びて取れてしまって、雨が降ると樋がくぼみ、そこに両方から雨が集中して、そこから直接、庭に雨水が落ちるようになっている。樋をつたって側溝に雨水を処理できないのである。古い家なので金をかけて修理する気は起らず、そのままにしてきたが、最近の台風の時など、こちらの2階から見ていると、さすがに修理しようと思うようになった。
背の高い(2メートルほど)脚立があればできるのではないかと思っていた。なかなか思い切れなかったが、先週、他にも用途がある(樹木の剪定など)と思って、思い切って購入した。今週はそれを使って、雨樋の応急処置を行った。最初は留め金で固定するつもりだったが、針金でも固定できることに気づいて、針金で処理した。
明日は雨の予報である。雨水は樋をつたって、側溝に流れていくだろうか。
背の高い(2メートルほど)脚立があればできるのではないかと思っていた。なかなか思い切れなかったが、先週、他にも用途がある(樹木の剪定など)と思って、思い切って購入した。今週はそれを使って、雨樋の応急処置を行った。最初は留め金で固定するつもりだったが、針金でも固定できることに気づいて、針金で処理した。
明日は雨の予報である。雨水は樋をつたって、側溝に流れていくだろうか。










 (1)
(1)


 のx=0における微分の値が1であることを示している。
のx=0における微分の値が1であることを示している。
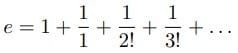
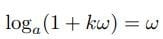


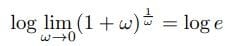


 (1)
(1) (2)
(2) (3)
(3)
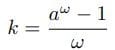
 >1である。
>1である。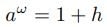 (1)
(1)
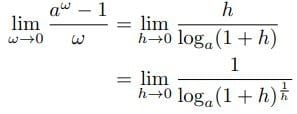 (2)
(2)
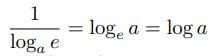


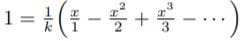

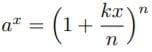
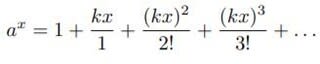




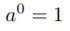
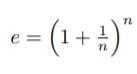

 の無限級数表示、双曲線の下の面積(メルカトルの公式)を「算術的な世界」(志賀浩二)から把握した。これらは冪から構築した指数関数と対数関数を検証する道筋に位置づいている。
の無限級数表示、双曲線の下の面積(メルカトルの公式)を「算術的な世界」(志賀浩二)から把握した。これらは冪から構築した指数関数と対数関数を検証する道筋に位置づいている。