昨日書いた「『天地明察』の問題は誤植か否か?」の記事に早くもコメントを寄せてもらい大きく進展したので改めて記事に。本当にありがたいことです<(_ _)>
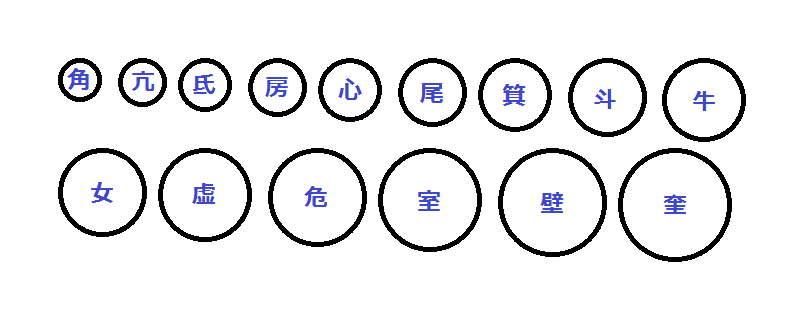
本屋大賞を受賞した『天地明察』236ページ掲載の招差術の問題は以下の通り。
もっもさんに、この問題が渋谷の金王八幡神社所蔵の算額を元にしているのではと指摘していただき、更にcobozeさんにその問題の内容及び解法の情報を提示していただいた。
鳴門教育大学情報教育ジャーナル
情報教育の視点から見た和算に関する考察(菊地章氏,井出健治氏)
http://www.naruto-u.ac.jp/journal/info-edu/j05006.pdf
そこに掲載されている算額の問題は、
であり、『天地明察』の問題とは数字のみ異なっている。
角星+亢星=16寸(10寸)
心星+尾星+箕星=30寸(27寸5分)
虚星+危星+室星+壁星+奎星=63寸(40寸)
※カッコ内は『天地明察』の問題
算額では、それぞれの数値を宿星の数で割ると、8寸、10寸、12.6寸と増大している。宿星が大きくなるのだから当然。一方、『天地明察』の問題では、5寸、9.17寸、8寸となっており、明らかに誤謬が存在している。
算額の解法は以下の通り。


『天地明察』の問題をこれに当てはめてcobozeさんが解いてくれたのが、4.3512773722627737226277372262774...だそうです。ごめんなさい、行列方程式は習ってません(多分)。頑張って、後で筆算したいと思ってますが^^;
cocoさんの御指摘から始まった招差術問題も皆様の御力によりかなり進展しています。『天地明察』掲載の問題は誤謬の可能性が非常に高く感じられますが、他の可能性などございましたら、是非御指摘くださいますようお願いします。
※「算額の解法」はリンク先のPDFから引用したものですが、誤植等があります。詳しくはコメント欄をお読みください。
※文庫版およびコミック版では問題が修正されているようで、その解についてはコメント欄に記載。
本屋大賞を受賞した『天地明察』236ページ掲載の招差術の問題は以下の通り。

今、図の如く、大小の十五宿の星の名を持つ円が並んでいる。角星と亢星の周の長さを足すと十寸である。また心星と尾星と箕星の周の長さを足すと二十七寸五分である。さらに虚星、危星、室星、壁星、奎星の五つの星の周の長さを足すと四十寸である。角星の周の長さは何寸であるか問う
もっもさんに、この問題が渋谷の金王八幡神社所蔵の算額を元にしているのではと指摘していただき、更にcobozeさんにその問題の内容及び解法の情報を提示していただいた。
鳴門教育大学情報教育ジャーナル
情報教育の視点から見た和算に関する考察(菊地章氏,井出健治氏)
http://www.naruto-u.ac.jp/journal/info-edu/j05006.pdf
そこに掲載されている算額の問題は、
今有如圓宿名一十五球
只云角亢二球周寸相併
一十六寸又云心尾箕三
球周寸相併三十寸重云
虚危室壁奎五球周寸相
併六十三寸問角球周寸
幾何
であり、『天地明察』の問題とは数字のみ異なっている。
角星+亢星=16寸(10寸)
心星+尾星+箕星=30寸(27寸5分)
虚星+危星+室星+壁星+奎星=63寸(40寸)
※カッコ内は『天地明察』の問題
算額では、それぞれの数値を宿星の数で割ると、8寸、10寸、12.6寸と増大している。宿星が大きくなるのだから当然。一方、『天地明察』の問題では、5寸、9.17寸、8寸となっており、明らかに誤謬が存在している。
算額の解法は以下の通り。


『天地明察』の問題をこれに当てはめてcobozeさんが解いてくれたのが、4.3512773722627737226277372262774...だそうです。ごめんなさい、行列方程式は習ってません(多分)。頑張って、後で筆算したいと思ってますが^^;
cocoさんの御指摘から始まった招差術問題も皆様の御力によりかなり進展しています。『天地明察』掲載の問題は誤謬の可能性が非常に高く感じられますが、他の可能性などございましたら、是非御指摘くださいますようお願いします。
※「算額の解法」はリンク先のPDFから引用したものですが、誤植等があります。詳しくはコメント欄をお読みください。
※文庫版およびコミック版では問題が修正されているようで、その解についてはコメント欄に記載。

















p = -59/1280
q = 4823/3840
r = 997/240
となってしまうのですが(ー∇ー;)
そもそもこの行列方程式の立て方すら理解できていないので混沌状態ですが・・・
PDFにも、残念ながら、誤植があります。
|p| | 5 3 2|-1 |16|
|q|=|110 18 3| |30|
|r| |855 65 5| |63|
だと思います。
an = pn^2 + qn + r を想定する。
a1 = p + q + r
a2 = 4p + 2q + r
:
a5 = 25p + 5q + r
a6 = 36p + 6q + r
a7 = 49p + 7q + r
:
a11 = 121p + 11q + r
a12 = 144p + 12q + r
a13 = 169p + 13q + r
a14 = 196p + 14q + r
a15 = 225p + 15q + r
a1+a2 = 5p + 3q + 2r = 16 ・・・(1)
a5+a6+a7 = 110p + 18q + 3r = 30 ・・・(2)
a11+a12+a13+a14+a15 = 855p + 65q + 5r = 63 ・・・(3)
(1)(2)(3)を行列方程式で表すと上の通りです。
excel にぶち込んで計算させると、
5 3 2
110 18 3
855 65 5
A^-1
0.00958 -0.01049 0.002464 16 -0.0063 69
-0.18385 0.153741 -0.0187 30 0.492245 -5395
0.751825 -0.20438 0.021898 63 7.277372 -79760
7.763321 -85086
-10960
-85086 / -10960 = 7.763321 と成ります。
「天地明察」の問題にも適用してみましたが、30/7にも、4.5 にもなりません。もう少し考えてみます。
とりあえず、お知らせまで。
斗星が含まれている場合の角星の半径=4.766509434...
房星が含まれていた場合の角星の半径=4.705947137...
となってやっぱり4.5にはなりません
計算はExel先生にやってもらいましたw
誤植というよりも、検証しないで掲載しちゃってるんでしょうか?
それとも解法が違うのか、これ以上はわかりませんねぇ・・・
はじめまして。
非常に分かりやすい解説ありがとうございます。
PDFの誤植の件も理解しました。私もExcelで計算して確認しました。
「天地明察」の問題は、間違っているのは明らかですが、どう間違えたのかは分かりにくいですね。「一般項を想定した連立方程式」という考え方ではないというのも、参考にした算額の問題との兼ね合いから考えにくいですし。
>cobozeさん
途中の計算過程というリクエストに応えてくださってありがとうございますw
式の立て方を理解すれば、解法も行列方程式にこだわらなくていいと分かりました^^;
Excelでの計算ができるので、行列方程式の利点も知りましたが。
勾股弦の問題の解である「30/7」になるように算額の問題を改変して掲載しているはずなのですが、誰も検証しなかったのか本当に不思議です。
私もこの問題は流し読みしかしなかったので大きなことは言えませんが、cocoさんの指摘は非常に明確なものでした。
ちなみに、「天地明察」の数字をそのままで計算すると、牛星が最大で、そこからは星が小さくなっていき、最大のはずの奎星は3番目の氐星よりも小さくなりますね。
既に5刷で、本屋大賞受賞により更に増刷もかかると思いますが、これまで修正されなかったのが不思議です。ネット上での指摘がほとんど見られないので、気付いた人はごく少数なのでしょうが……。
解を「30/7」あるいは「4.5」となるように算額の問題をどう改変すればよかったかあたりが今後の考えどころでしょうか。
40寸を49寸にすれば
答えは4.5になり、円の大小関係も正しくなりますが
こりゃ無理矢理すぎますかね。
1 - 4.5
2 - 5.5
3 - 6.4
4 - 7.2
5 - 7.9
6 - 8.5
7 - 9.0
8 - 9.4
9 - 9.7
10 - 9.9
11 -10.0
12 - 10.0
13 - 9.9
14 - 9.7
15 - 9.4
と12番目の危星から縮んでしまいますが。
それでも元の問題よりも遥かに狙いに合致してますw
元の問題は出だしのところ(27.5/3<40/5になってない時点で無術ですしね)からおかしいですし、普通に解けば解も合っていませんし、ヌルハチさんの設定の方が良かったですねw
大小関係を保つには最初の10寸も変えないと無理そうです(ー∇ー;)
ってことになりますね・・・。
角星+亢星= x
心星+尾星+箕星= y
虚星+危星+室星+壁星+奎星= z
とすると、
p = 105/10960・x - 115/10960・y + 27/10960・z
q = -1209/6576・x + 1011/6576・y - 123/6576・z
となり、代入すると
1/10960 ( (210n - 2015)x - (230n - 1685)y + (54n - 205)z ) > 0
両辺を10960倍して、
(210n - 2015)x - (230n - 1685)y + (54n - 205)z > 0
n=1 -1805x + 1455y - 151z > 0
n=2 -1595x + 1225y - 97z > 0
n=3 -1385x + 995y - 43z > 0
n=4 -1175x + 765y + 11z > 0
n=5 -965x + 535y + 65z > 0
n=6 -755x + 305y + 119z > 0
n=7 -545x + 75 y + 173z > 0
n=8 -335x - 155y + 227z > 0
n=9 -125x - 385y + 281z > 0
n=10 85x - 615y + 335z > 0
n=11 295x - 845y + 389z > 0
n=12 505x - 1075y + 443z > 0
n=13 715x - 1305y + 497z > 0
n=14 925x - 1535y + 551z > 0
n=15 1135x - 1765y + 605z > 0
まあここから何が見えるかは分かりませんがw
p15 でした…
27.5→44, 40→250 だとa15がa1に比べて大きくなりすぎる。
著者も数字をいじるのを諦めて妥協したのでしょうかね?それでも4.5は意味がわからん。