「感想:『天地明察』」の記事で取り上げた算術の問題が解決したので改めて記事を書く。解決はcobozeさん、Fakirさんの多大なご協力があってが故のことである(というか、私自身は確認するだけだった orz)。改めて両氏に感謝の意を記しておきたい。
冲方丁の小説『天地明察』の20ページ前後に記された問題は以下の通り。
『今、図のごとく釣(高さ)が9寸、股(底辺)が12寸の勾股弦(直角三角形)があり、内部に直径が等しい円を二つ入れる。円の直径はいくらか。』

答えは30/7寸と書かれていた。また、その答えを導いた計算方法も書かれてはいたが、問題を見たときに考えた解き方とその式とはかけ離れていた。
図をまず以下のものとする。青字は線分の長さを示す。
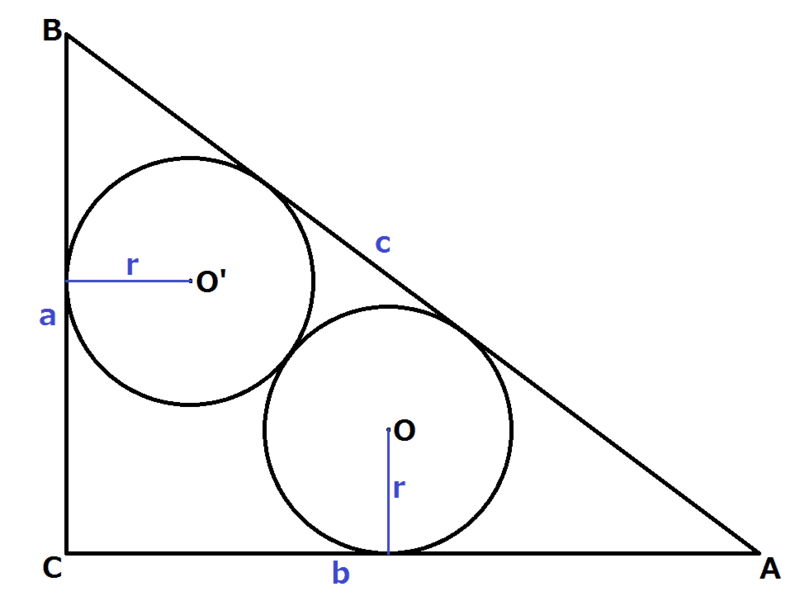
計算方法は、{ 2ab / ( a + b + c ) } ・ { c / ( a + b ) }というものだった。
■面積を分割して解く方法
cobozeさんがOKWaveの質問の中から見つけてくれた方法。質問は直角三角形ではないが、解法は変わらない。

△ABCの面積は ab / 2 = 54
△ABC = △AOC + △COO' + △BCO' + □ABOO' ・・・①
△AOC = br / 2 = 6r
△BCO' = ar / 2 = 9/2・r
□ABOO' = ( 2r + c ) * r / 2 = r^2 + 15/2・r
△COO'はOO'を底辺とすると、△ABCで底辺をABとした場合の高さから r を引いたものが高さとなる。△ABCで底辺をABとした場合の高さを h とすると、ch / 2 が△ABCの面積となる。15/2・h = 54 なので、h =36 / 5 。よって、△COO'の高さは、36 / 5 - r となる。
△COO' = 2r( 36/5 - r ) / 2 =36/5・r - r^2
①に代入すると、
54 = 6r + 9/2・r + r^2 + 15/2・r + 36/5・r - r^2
126/5・r = 54
r = 270/126 = 15/7
求めたのは直径なので、これを2倍した 30/7 で明察となる。
しかし、解法の式とは合致しない。
■相似から解く方法
Fakirさんが示してくれた△ABCと△OO'Zの比から解く方法。

OとO'からACとBCに垂線を下ろす。OからBCへの垂線とO'からACへの垂線の交点をZとする。△OO'Zは△ABCと相似である。OZを x 、O'Zを y とする。また、OからACへの垂線とACとの交点をPとし、線分APの長さを p 、O'からBCへの垂線とBCとの交点をQとし、線分BQの長さを q とする。
辺AC = p + x + r = 12
辺BC = q + y + r = 9
辺AB = p + 2r + q = 15 ・・・①
p = 12 - x - r 、q = 9 - y - r として①に代入すると、
( 12 - x - r ) + 2r + ( 9 - y - r ) = 15
x + y =6
相似から、x :y = 9 :12 なので、y = 12/9・x となる。代入すると、
x + 12/9・x = 6
21/9・x = 6
x = 54/21 = 18/7
これより、y =24/7 となる。
三平方の定理より、
x^2 + y^2 = (2r)^2
(18/7)^2 + (24/7)^2 = 4r^2
r^2 = ( 324 + 576 ) / 49 / 4 = 225 / 49 = ( 15 / 7 )^2
r は正なので、r = 15/7 となる。直径は2倍なので30/7で明察。
■辺の長さから解く方法
これは相似から解く方法をシンプルにしたもので、Fakirさんが提示してくれたもの。

図も相似のものと同じ。x と y を相似から r と a 、b を使って表す。
x :2r = b :c
x = 2r・b/c
y :2r = a :c
y = 2r・a/c
これにより、
辺AC = p + 2r・b/c + r = 12
辺BC = q + 2r・a/c + r = 9
p = 12 - 13/5・r
q = 9 - 11/5・r
辺AB = p + 2r + q = 15 に代入して、
12 - 13/5・r + 2r + 9 - 11/5・r = 15
14/5・r = 6
r =30/14 = 15/7
■三角形の内接円の公式から迫る

図のように内接する円が1つの場合、
△ABC = △ABO + △BCO + △ACO
ab / 2 = cr / 2 + ar / 2 + br / 2
ab = ( a+ b + c ) r
r = ab / ( a+ b + c )
これは、解法の式 { 2ab / ( a + b + c ) } ・ { c / ( a + b ) } と全く同じである(直径なので2倍されている)。
ここでcobozeさんの鋭い洞察があった。

この黄色い部分を合わすと、

片方の円だけを内接する三角形と同じものとなる。
△ABCに一つだけ内接する円を想定し、その半径を R とする。
R :r =c :c - 2r
r = ( c - 2r ) / c ・R
cr = cR - 2rR
( c + 2R ) r = cR
r = cR / ( c + 2R )
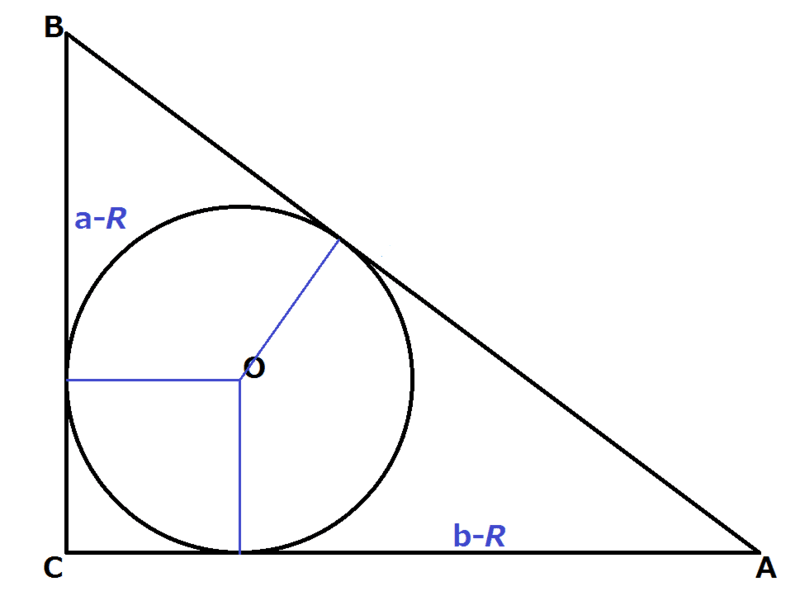
上図より、
c = a - R + b - R = a + b - 2R
これを代入して、
r = cR / ( a + b - 2R + 2R )
r = R ・ c / ( a + b )
R = ab / ( a+ b + c ) より、
r = { ab / ( a+ b + c ) }・{ c / ( a + b) }
2r = { 2ab / ( a+ b + c ) }・{ c / ( a + b) }
となり、式の謎が解けた。
答えは一つでも、その解き方は多種多様。それが数学の面白さでもある。今回の問題では考えるのは人任せになってしまったがそれでも楽しめた(笑)。数学的ひらめきと論理の積み重ねで答えに迫っていく喜びは悩んでこそ得られるものだろう。
小説の本筋ではなかったせいか、中学レベルの問題(?)だったせいか、小説内で詳しい説明がなかったことが結果として楽しみの種となった。そこまで著者の仕掛けだとは考えにくいが、いい問題だったのは確かだ。
コメント用に図を追加


図9

冲方丁の小説『天地明察』の20ページ前後に記された問題は以下の通り。
『今、図のごとく釣(高さ)が9寸、股(底辺)が12寸の勾股弦(直角三角形)があり、内部に直径が等しい円を二つ入れる。円の直径はいくらか。』

答えは30/7寸と書かれていた。また、その答えを導いた計算方法も書かれてはいたが、問題を見たときに考えた解き方とその式とはかけ離れていた。
図をまず以下のものとする。青字は線分の長さを示す。

計算方法は、{ 2ab / ( a + b + c ) } ・ { c / ( a + b ) }というものだった。
■面積を分割して解く方法
cobozeさんがOKWaveの質問の中から見つけてくれた方法。質問は直角三角形ではないが、解法は変わらない。

△ABCの面積は ab / 2 = 54
△ABC = △AOC + △COO' + △BCO' + □ABOO' ・・・①
△AOC = br / 2 = 6r
△BCO' = ar / 2 = 9/2・r
□ABOO' = ( 2r + c ) * r / 2 = r^2 + 15/2・r
△COO'はOO'を底辺とすると、△ABCで底辺をABとした場合の高さから r を引いたものが高さとなる。△ABCで底辺をABとした場合の高さを h とすると、ch / 2 が△ABCの面積となる。15/2・h = 54 なので、h =36 / 5 。よって、△COO'の高さは、36 / 5 - r となる。
△COO' = 2r( 36/5 - r ) / 2 =36/5・r - r^2
①に代入すると、
54 = 6r + 9/2・r + r^2 + 15/2・r + 36/5・r - r^2
126/5・r = 54
r = 270/126 = 15/7
求めたのは直径なので、これを2倍した 30/7 で明察となる。
しかし、解法の式とは合致しない。
■相似から解く方法
Fakirさんが示してくれた△ABCと△OO'Zの比から解く方法。

OとO'からACとBCに垂線を下ろす。OからBCへの垂線とO'からACへの垂線の交点をZとする。△OO'Zは△ABCと相似である。OZを x 、O'Zを y とする。また、OからACへの垂線とACとの交点をPとし、線分APの長さを p 、O'からBCへの垂線とBCとの交点をQとし、線分BQの長さを q とする。
辺AC = p + x + r = 12
辺BC = q + y + r = 9
辺AB = p + 2r + q = 15 ・・・①
p = 12 - x - r 、q = 9 - y - r として①に代入すると、
( 12 - x - r ) + 2r + ( 9 - y - r ) = 15
x + y =6
相似から、x :y = 9 :12 なので、y = 12/9・x となる。代入すると、
x + 12/9・x = 6
21/9・x = 6
x = 54/21 = 18/7
これより、y =24/7 となる。
三平方の定理より、
x^2 + y^2 = (2r)^2
(18/7)^2 + (24/7)^2 = 4r^2
r^2 = ( 324 + 576 ) / 49 / 4 = 225 / 49 = ( 15 / 7 )^2
r は正なので、r = 15/7 となる。直径は2倍なので30/7で明察。
■辺の長さから解く方法
これは相似から解く方法をシンプルにしたもので、Fakirさんが提示してくれたもの。

図も相似のものと同じ。x と y を相似から r と a 、b を使って表す。
x :2r = b :c
x = 2r・b/c
y :2r = a :c
y = 2r・a/c
これにより、
辺AC = p + 2r・b/c + r = 12
辺BC = q + 2r・a/c + r = 9
p = 12 - 13/5・r
q = 9 - 11/5・r
辺AB = p + 2r + q = 15 に代入して、
12 - 13/5・r + 2r + 9 - 11/5・r = 15
14/5・r = 6
r =30/14 = 15/7
■三角形の内接円の公式から迫る

図のように内接する円が1つの場合、
△ABC = △ABO + △BCO + △ACO
ab / 2 = cr / 2 + ar / 2 + br / 2
ab = ( a+ b + c ) r
r = ab / ( a+ b + c )
これは、解法の式 { 2ab / ( a + b + c ) } ・ { c / ( a + b ) } と全く同じである(直径なので2倍されている)。
ここでcobozeさんの鋭い洞察があった。

この黄色い部分を合わすと、

片方の円だけを内接する三角形と同じものとなる。
△ABCに一つだけ内接する円を想定し、その半径を R とする。
R :r =c :c - 2r
r = ( c - 2r ) / c ・R
cr = cR - 2rR
( c + 2R ) r = cR
r = cR / ( c + 2R )

上図より、
c = a - R + b - R = a + b - 2R
これを代入して、
r = cR / ( a + b - 2R + 2R )
r = R ・ c / ( a + b )
R = ab / ( a+ b + c ) より、
r = { ab / ( a+ b + c ) }・{ c / ( a + b) }
2r = { 2ab / ( a+ b + c ) }・{ c / ( a + b) }
となり、式の謎が解けた。
答えは一つでも、その解き方は多種多様。それが数学の面白さでもある。今回の問題では考えるのは人任せになってしまったがそれでも楽しめた(笑)。数学的ひらめきと論理の積み重ねで答えに迫っていく喜びは悩んでこそ得られるものだろう。
小説の本筋ではなかったせいか、中学レベルの問題(?)だったせいか、小説内で詳しい説明がなかったことが結果として楽しみの種となった。そこまで著者の仕掛けだとは考えにくいが、いい問題だったのは確かだ。
コメント用に図を追加


図9


















辺AC = p + 2r・b/c + r = b
辺BC = q + 2r・a/c + r = a
辺AB = q + 2r + p = c
⇔
p = {(-a+b+c)/(a+b+c)}・r
q = {(a-b+c)/(a+b+c)}・r
追加のコメント(?)ですが、
(a+b) : c
という比は三平方の定理を考えると
一辺の長さが c の正方形に対して辺の長さがa,b,cの三角形を4つ外に書いてできる正方形のさらに外側に三角形作った場合の正方形ですね。
(一辺の長さがa+bの正方形)
ということはひとつの内接円の場合はこの三角形の内接円の半径となる・・・。何でそうなるかがわからないorz
中学生の幾何レベルの問題ですが、数学的に考えるには高校の平面図形あたりを勉強しなおさないとだめなのかな。。
(ベクトルと複素数はやったけど、平面図形はほとんどやらなかったorz)
一辺がa+bの正方形はa,b,cの長さの三角形4枚からできる正方形で、その外側にさらに三角形書いた場合に、その三角形の内接円の半径が
{ab・(a+b)}/{c・(a+b+c)}
になっていて、これに c/(a+b)をかけると、最初の三角形の内接円の半径になっていて
元の問題の(二つ)内接円の半径と、三角形の(ひとつの)内接円の半径の比が出てくるということです。
q = {(a-b+c)/(a+b-c)}・r
です・・
その内側の斜めの正方形は、一辺の長さが c
青色の正方形は、一辺の長さが c・c / ( a + b)
つまり、c / ( a + b ) 倍ずつになっています。
2つ内接する円の半径は、青色の円の半径と同じ。
ここから更に何が言えるかは分かりませんが、まだ何か見えてきそうで面白いですねw
以下略・・・。
いきなり式書いて、読者に分かれってことはこんな感じで図から直観的にわかると考えるべきなのかな。
図としては最も直感的に分かりやすい形だと思います。ただ平行四辺形からこの図がすぐに思い付くかどうかは難しそうにも思えます。
面積などから求めるより、c / ( a + b ) という比から求めた方が図のような発展性はありますが、第一感の求め方じゃないと思いますねw
折り返せばいいことに気がつきました。ピンクの三角形の左側は、下にちょっと突き出して三角形作ればこれも合同(青い内接円の書いてある三角形をこの線で折り返したもの)
なので、この円が内接円が二つの場合の、内接円であることがこれで証明できて(同じ大きさであることが分かる)、半径求めて終わり。
この場合、この図が直感的に出てくるというより、説明のときに、ほらこのとおり的な感じで使うのかなと。
自分が中学生だったら感心し、高校生なら反発を覚え、いまならおいおいと突っ込みを入れますがw
単純に考えると箕星の周長は九寸以上(27.5÷3より)となり、虚星は箕星より大きいので虚星の周長は九寸以上と考えられ、とすると虚星以上の5個の星の周長は最低でも四十五寸(9×5)以上となってしまうと思うのですが…
問題文の読み方自体が間違っているのかなとも思っています。
本ブログでは一問目に対して素晴らしい考察を加えているように感じられましたのでこのような質問をさせていただきました。
もしよろしければご回答いただけたらと思います。よろしくお願いします。
27寸5分の星が3つではなく4つなら……などと感じましたが、近いうちに立ち読みでもしてまずは本文を確認してみたいと思います^^;
本屋大賞にノミネートされるなど話題になっている作品なのに、作品内の数学の問題について触れたブログなどはほとんど見かけません。
この問題はストーリー上かなり重要な問題であるにもかかわらず、解答が直後に書かれているせいか真剣に考えることなく流してしまいがちなのかもしれません(私がそうでした)。
現時点では誤植の可能性が高いと思いますが、より多くの人の目に触れるためにも新たに記事としてこの問題を取り上げたいと思います。どなたか詳しい方の目に留まれば……。
これは「三角形の内接円の公式から迫る」の図より、
AE = p + r
DE = q + r
AB = p + q + 2r
から導くことができる。
△ADEと△ABCの比は、
AE + DE : AC + BC = 15 : 21
△ABCの内接円の直径は6寸なので、
2r : 6 = 15 : 21
2r = 30 / 7
図で考えないとなかなか理解できないので図を挿入してみました。
シンプルな解法があるんですね。
このピンク色の直角三角形は、元の直角三角形ABCと相似なので、先の分割点をXとすれば、それぞれの股ACと股AXの比 c/(a+b) を利用して、元の直角三角形ABCに一つだけ内接する場合の円の直径 2ab/(a+b+c)から求めることができます。
すなわち、春海の術の説明で、「勾股を相乗し、これを二段(二倍)。さらに、勾股弦の総和にて除(割る)。」が、一つだけ内接する場合の円の直径であり、「これに弦を乗(掛ける)し、また勾股の和にて除なり。」が、直角三角形の相似比で求めるということになります。
以上、拙い説明ですが、如何でしょうか?
それでは、春海がハゼ?の干物をお土産に、塾まで押し掛けた続きを読むことにします。
「股ACと股AXの比 c/(a+b) 」の出し方について悩みましたが、なんとか解決したと思います(決してスマートな解法ではないと思いますがw)。
春海の説明がようやく腑に落ちたように思います。本編にこれくらいの説明を載せてくれれば・・・と思いもしますが、蛇足とも言えますしね。
続きをどうぞ楽しんでください。
もうひとつの問題の方もブログで取り上げていますので、よろしければそちらもご覧ください。
この問題に対して、春海が間違えた解を出した方法が載っています。
本当に解き方は様々にあるのですねw
また、その参考として、中学校教師によるレポートがありました。
和算小説「天地明察」より
http://www2.ttcn.ne.jp/~nagai/waseda/wasan/tenchi.PDF
中学の教材としてアレンジするなど非常に興味深い内容でした。