前回の続き
統計解析フリーソフト R の備忘録頁 ver.3.1
http://cse.naro.affrc.go.jp/takezawa/r-tips/r.html
や
Rで統計 - R入門
http://home.hiroshima-u.ac.jp/chubo/index.cgi?R%a4%c7%c5%fd%b7%d7
をもとに、Rを勉強してみる
まずは、基本的な操作ということで、記述統計の世界をやってみる。
・データの確認
・1変数の基本的な統計量
・2変数の基本的な統計量(数値)
・2変数の基本的な統計量(選択肢)
についてみてみる
■データの確認
データの読み込みに関しては、別の機会にやることにして・・・
とにかく、データを読み込んだ、あるいは、Rに備え付けられているデータを利用するとする。
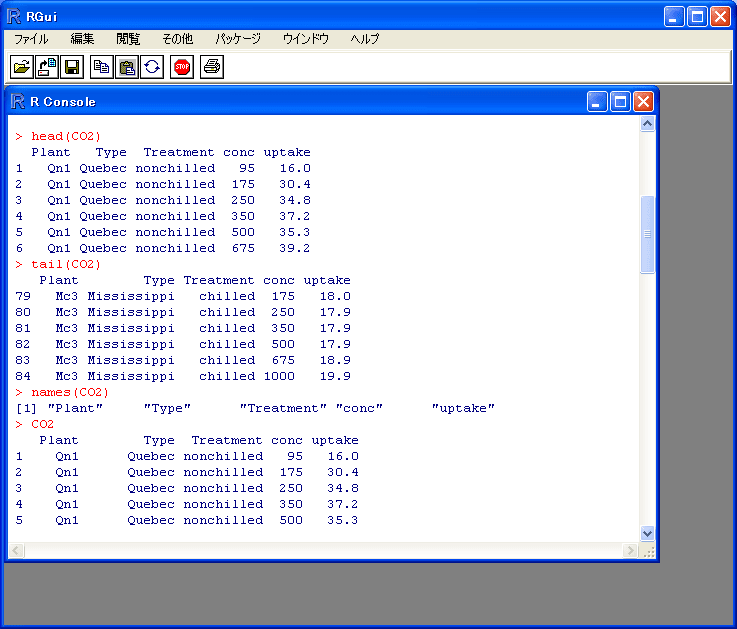
今回は、CO2というRに備え付けられているデータを利用する。
そのデータを確認したい場合は、
<<項目名を表示する>>
names(CO2)
<<先頭数行を表示>>
head(CO2)
<<終わり数行を表示>>
tail(CO2)
<<全体表示>>
CO2
こんなかんじ
■1変数の基本的な統計量
CO2$項目名 で、その項目のカラムすべてが取り出せる。
このカラムが、数値データの場合、以下のような平均、不偏分散、不偏分散の標準偏差、メジアンなどは、いかのように求められる。
<<平均>>
mean(CO2$conc)
<<不偏分散>>
var(CO2$conc)
<<不偏分散の標準偏差>>
sd(CO2$conc)
<<メジアン>>
median(CO2$conc)
不偏分散ではなく、分散と標準偏差を求めたい場合、不偏分散を(n-1)/n倍すれば求まる。
ここで、nは標本数なのだが、その標本数を求めるには
<<標本数>>
length(CO2$conc)
なお、summaryを使うと、
数値データに関しては、四分位点や、平均を求め、
選択肢を選ぶようなものに関しては、各選択肢の件数
が表示される
summary(CO2)

なお、数値しか表示できないmeanに、CO2と指定して、選択肢のデータも表示させようとすると

のように、警告が出る。
また、図で表示させたい場合は、
<<ヒストグラムを書く>>
hist(CO2$conc)

<<箱ひげ図を書く>>
boxplot(CO2$conc)

なんてことをする。
■2変数の基本的な統計量(数値)
2変数の関係を見たい場合、両方とも数値であれば、相関係数ないしは共分散をもとめ、散布図を書く。
<<相関係数>>
cor(CO2$conc,CO2$uptake)
<<共分散>>
cov(CO2$conc,CO2$uptake)
<<散布図>>
plot(CO2$conc,CO2$uptake)

■2変数の基本的な統計量(選択肢)
項目の場合は、クロス表を作る
<<クロス表>>
table(CO2$Type,CO2$Treatment)
そうすると、なんか図にしてくれる。
<<図にする>>
plot(CO2$Type,CO2$Treatment)

ちなみに、数値と選択肢の組み合わせの場合でplotすると
plot(CO2$Treatment,CO2$uptake)
こんな、項目毎の箱ひげ図を出してくれる。

また、ただCO2だけでプロットすると
plot(CO2)
こんなふうになる。

統計解析フリーソフト R の備忘録頁 ver.3.1
http://cse.naro.affrc.go.jp/takezawa/r-tips/r.html
や
Rで統計 - R入門
http://home.hiroshima-u.ac.jp/chubo/index.cgi?R%a4%c7%c5%fd%b7%d7
をもとに、Rを勉強してみる
まずは、基本的な操作ということで、記述統計の世界をやってみる。
・データの確認
・1変数の基本的な統計量
・2変数の基本的な統計量(数値)
・2変数の基本的な統計量(選択肢)
についてみてみる
■データの確認
データの読み込みに関しては、別の機会にやることにして・・・
とにかく、データを読み込んだ、あるいは、Rに備え付けられているデータを利用するとする。
今回は、CO2というRに備え付けられているデータを利用する。
そのデータを確認したい場合は、
<<項目名を表示する>>
names(CO2)
<<先頭数行を表示>>
head(CO2)
<<終わり数行を表示>>
tail(CO2)
<<全体表示>>
CO2
こんなかんじ

■1変数の基本的な統計量
CO2$項目名 で、その項目のカラムすべてが取り出せる。
このカラムが、数値データの場合、以下のような平均、不偏分散、不偏分散の標準偏差、メジアンなどは、いかのように求められる。
<<平均>>
mean(CO2$conc)
<<不偏分散>>
var(CO2$conc)
<<不偏分散の標準偏差>>
sd(CO2$conc)
<<メジアン>>
median(CO2$conc)
不偏分散ではなく、分散と標準偏差を求めたい場合、不偏分散を(n-1)/n倍すれば求まる。
ここで、nは標本数なのだが、その標本数を求めるには
<<標本数>>
length(CO2$conc)
なお、summaryを使うと、
数値データに関しては、四分位点や、平均を求め、
選択肢を選ぶようなものに関しては、各選択肢の件数
が表示される
summary(CO2)

なお、数値しか表示できないmeanに、CO2と指定して、選択肢のデータも表示させようとすると

のように、警告が出る。
また、図で表示させたい場合は、
<<ヒストグラムを書く>>
hist(CO2$conc)

<<箱ひげ図を書く>>
boxplot(CO2$conc)

なんてことをする。
■2変数の基本的な統計量(数値)
2変数の関係を見たい場合、両方とも数値であれば、相関係数ないしは共分散をもとめ、散布図を書く。
<<相関係数>>
cor(CO2$conc,CO2$uptake)
<<共分散>>
cov(CO2$conc,CO2$uptake)
<<散布図>>
plot(CO2$conc,CO2$uptake)

■2変数の基本的な統計量(選択肢)
項目の場合は、クロス表を作る
<<クロス表>>
table(CO2$Type,CO2$Treatment)
そうすると、なんか図にしてくれる。
<<図にする>>
plot(CO2$Type,CO2$Treatment)

ちなみに、数値と選択肢の組み合わせの場合でplotすると
plot(CO2$Treatment,CO2$uptake)
こんな、項目毎の箱ひげ図を出してくれる。

また、ただCO2だけでプロットすると
plot(CO2)
こんなふうになる。













 ウィリアムのいたずら @xmldtp
ウィリアムのいたずら @xmldtp



