トライソープ、トライスープ、トリスープ

 

　［トライソープ方式］
　本実施の形態に係る符号化装置は、トライソープ（ＴｒｉＳｏｕｐ：Ｔｒｉａｎｇｌｅ－Ｓｏｕｐ）方式を用いて位置情報を符号化する。

　トライソープ方式は、点群データの位置情報を符号化する方式の一つであり、不可逆圧縮方式である。トライソープ方式では、処理対象の元点群を三角形の集合に置き換え、その平面上に点群を近似する。具体的には、元点群をノード内の頂点情報に置き換え、頂点同士を結んで三角形群を生成する。また、三角形を生成するための頂点情報がビットストリームに格納され、復号装置へ送られる。

　まず、トライソープ方式を用いた符号化処理について説明する。図１は、元点群の例を示す図である。図１に示すように、対象物の点群１０２は、対象空間１０１に含まれ、複数の点１０３を含む。

　初めに、符号化装置は、元点群を所定の深さ（ｄｅｐｔｈ）まで８分木（Ｏｃｔｒｅｅ）分割する。８分木分割では、対象空間が８個のノード（サブ空間）に分割され、各ノードに点群が含まれるか否かを示す８ビットの情報（オキュパンシー符号）が生成される。また、点群が含まれるノードは、さらに、８個のノードに分割され、当該８個のノードの各々に点群が含まれるか否かを示す８ビットの情報が生成される。この処理が、予め定められた階層まで繰り返される。

　ここで、通常の８分木符号化では、例えば、ノードに含まれる点群の数の１つ又は閾値以下になるまで分割が繰り返される。一方、トライソープ方式は、８分木分割は途中の階層まで行われるが、当該階層以下の階層に対しては行われない。このような途中の階層までの８分木を、剪定８分木と呼ぶ。

　図２は、剪定８分木の例を示す図である。図２に示すように、点群１０２は、剪定８分木の複数のリーフノード１０４（最下層のノード）に分割される。

　次に、符号化装置は、剪定８分木のリーフノード１０４の各々に対して以下の処理を行う。なお、以下では、リーフノードを単にノードとも記す。符号化装置は、ノードのエッジ（ｅｄｇｅ）に近い点群の代表点として、エッジ上に頂点を生成する。この頂点をエッジ頂点と呼ぶ。例えば、エッジ頂点は、複数のエッジ（例えば平行な４辺）の各々に対して生成される。

　図３は、リーフノード１０４を二次元表示した例であり、例えば、図１に示すｚ方向から見たｘｙ平面を示す図である。図３に示すように、リーフノード１０４内の複数の点１１１のうちエッジの近接点に基づき、エッジ上にエッジ頂点１１２が生成される。

　なお、図３では、リーフノード１０４の外周の点線がエッジである。また、この例ではエッジとの距離が１以内の点（図３における範囲１１３に含まれる点）の位置の重み付き平均の位置にエッジ頂点１１２が生成される。なお、距離の単位は例えば点群の分解能であるが、これに限らない。また、この距離（閾値）は、この例では１であるが、１以外でもよく、可変であってもよい。

　次に、符号化装置は、複数のエッジ頂点を含む平面の法線方向に存在する点群に基づき、ノードの内部にも頂点を生成する。この頂点をセントロイド（ｃｅｎｔｒｏｉｄ）頂点と呼ぶ。

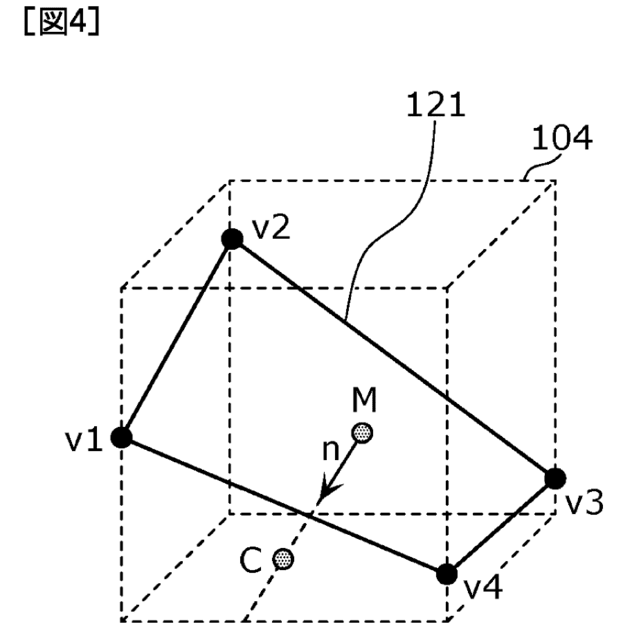
　図４及び図５は、セントロイド頂点の生成方法を説明するための図である。まず、符号化装置は、エッジ頂点群の中から例えば４点を代表点として選択する。図４に示す例ではエッジ頂点ｖ１～ｖ４が選択される。次に、符号化装置は、４点を通る近似平面１２１を算出する。次に、符号化装置は、近似平面１２１の法線ｎと、４点の平均座標Ｍとを算出する。次に、符号化装置は、平均座標Ｍから法線ｎの方向に延びる半直線に近い１以上の点（例えば図５に示す範囲１２２に含まれる点）の重み付き平均座標にセントロイド頂点Ｃを生成する。