離心円上の任意の点Kから長軸HIに垂線KLを下ろすとき、この垂線は点Mにおいて同じ比1:√(1-e2)に分割される。これはアポロニウスの楕円に対応させた楕円軌道の証明である。これは『新天文学』(1609年)の証明で、「楕円軌道の証明1」で示した。ケプラーはその後、太陽を楕円の焦点に位置づけた。そして楕円の性質「2つの焦点から楕円上の任意の点に引かれた線分の和は、つねに長径に等しい」に対応させる証明も可能になった。こちらは「楕円軌道の証明3」でみている。
下図(「ケプラーの第1法則(楕円軌道)の証明」、山本義隆『世界の見方の転換』3)で離心円の直径をKK'(長径)とする。K、K'から長軸線に下した垂線が楕円と交わる点をM、M'とすると、
離心円の半径を1、離心率をeとする。また、NとN'は焦点である。NM+N'M=2を証明する。
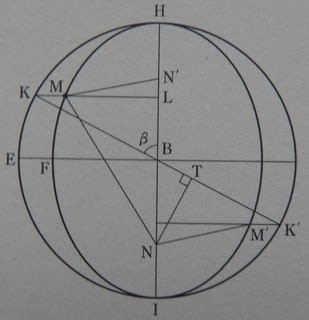
△MNLに着目して、
NM2=NL2+ML2
ここで
NL=e+cosβ
ML=√(1-e2)・sinβ (注)
より、
NM2
=(e+cosβ) 2+(1-e2)sin2β
=e2+2ecosβ+cos2β+sin2β-e2sin2β
ここでcos2β+sin2β=1だから、
=1+2ecosβ+e2(1-sin2β)
=1+2ecosβ+e2cos2β
=(1+ecosβ)2
したがって、
NM=1+ecosβ
同じように、△MN'Lに着目して、
N'M2=N'L2+ML2
ここで
N'L=e-cosβ
ML=√(1-e2)・sinβ
より、
N'M2
=(e-cosβ) 2+(1-e2)sin2β
=e2+2ecosβ+cos2β+sin2β-e2sin2β
=1-2ecosβ+e2(1-sin2β)
=1-2ecosβ+e2cos2β
=(1-ecosβ)2
したがって、
N'M=1-ecosβ
したがって、
NM+N'M=(1+ecosβ)+(1-ecosβ)=2
点Mは2点NとN'を焦点とする楕円上の点である。
図の長径HI=KK'と対応させておこう。

NM=1+ecosβ
=KB+BT=KT
また、N'M=1-ecosβ
=K'B-ecosβ
=K'B-BT=K'T
したがって、
NM+N'M=KT+TK'=KK'
(注)「楕円軌道の証明1」参照
下図(「ケプラーの第1法則(楕円軌道)の証明」、山本義隆『世界の見方の転換』3)で離心円の直径をKK'(長径)とする。K、K'から長軸線に下した垂線が楕円と交わる点をM、M'とすると、
NM+N'M=NM+NM'=KT+TK'=KK'であることをみた。これは『新天文学』にはなかった証明である。しかし、これぱ幾何学的なものだったので、ここでは代数的にみておこう。
離心円の半径を1、離心率をeとする。また、NとN'は焦点である。NM+N'M=2を証明する。

△MNLに着目して、
NM2=NL2+ML2
ここで
NL=e+cosβ
ML=√(1-e2)・sinβ (注)
より、
NM2
=(e+cosβ) 2+(1-e2)sin2β
=e2+2ecosβ+cos2β+sin2β-e2sin2β
ここでcos2β+sin2β=1だから、
=1+2ecosβ+e2(1-sin2β)
=1+2ecosβ+e2cos2β
=(1+ecosβ)2
したがって、
NM=1+ecosβ
同じように、△MN'Lに着目して、
N'M2=N'L2+ML2
ここで
N'L=e-cosβ
ML=√(1-e2)・sinβ
より、
N'M2
=(e-cosβ) 2+(1-e2)sin2β
=e2+2ecosβ+cos2β+sin2β-e2sin2β
=1-2ecosβ+e2(1-sin2β)
=1-2ecosβ+e2cos2β
=(1-ecosβ)2
したがって、
N'M=1-ecosβ
したがって、
NM+N'M=(1+ecosβ)+(1-ecosβ)=2
点Mは2点NとN'を焦点とする楕円上の点である。
図の長径HI=KK'と対応させておこう。

NM=1+ecosβ
=KB+BT=KT
また、N'M=1-ecosβ
=K'B-ecosβ
=K'B-BT=K'T
したがって、
NM+N'M=KT+TK'=KK'
(注)「楕円軌道の証明1」参照




















※コメント投稿者のブログIDはブログ作成者のみに通知されます