極微な冪指数と冪の表示2

極微な冪指数と冪の表示
　　
　　
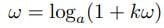
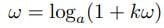
において、数kは底aに依存している。

a＝10のとき（常用対数）、ごくわずかだけ1を越える数、1＋1/1000000（百万分の1）の対数を求めてみると、
　　
となる。
　　kω＝1/1000000
より、
　　k＝1000000/43429＝2.30258
となる。

a＝10のとき、k=2.30258である。底が10のとき、冪指数ωの増大に対して、冪は2.3ω増大していく関係である。

底aとして他の数を設定すると、kには別の値が生じる。逆にkの値に対して別の底aも設定できる。冪指数ωの増大に対して、冪もωだけ増大していく関係ではk＝1である。このときの底が「自然対数もしくは双曲線対数の底」（e）である。すなわち、
　　
　　
である。