1 指数関数の無限級数表示
117節でオイラーは「底aと比kと変数zが満たすべき関係」
 (1)
(1)
を基礎にして、与えられた底aと比k(自動的に決まる)のとき、任意の指数関数(指数量)の無限級数表示を導いている。
まず、 と設定する。
と設定する。
ここでaを対数の底にとると、

である。また、

だから、(1)より、

となる。nの代わりにlog bを用いると、
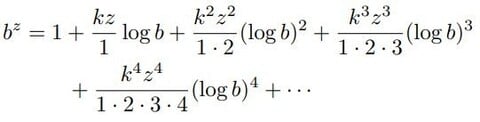
となる。
これが指数関数の無限級数表示である。「したがって、底aのある与えられた値から出発して文字kの値が知られたなら、任意の指数量bzが、zの冪指数が増大していく方向に進行する諸項をもつ無限級数を用いて表示されることになる。」
117節でオイラーは「底aと比kと変数zが満たすべき関係」
 (1)
(1)を基礎にして、与えられた底aと比k(自動的に決まる)のとき、任意の指数関数(指数量)の無限級数表示を導いている。
まず、
 と設定する。
と設定する。ここでaを対数の底にとると、

である。また、

だから、(1)より、

となる。nの代わりにlog bを用いると、
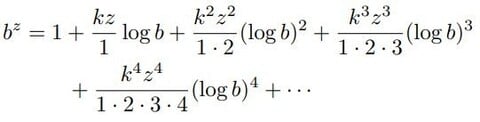
となる。
これが指数関数の無限級数表示である。「したがって、底aのある与えられた値から出発して文字kの値が知られたなら、任意の指数量bzが、zの冪指数が増大していく方向に進行する諸項をもつ無限級数を用いて表示されることになる。」









