アブダクション異聞2

パースのアブダクションへの疑問は、構成的理論と原理的理論をアインシュタインの思考モデルに位置づけたことにまで遡る（「構成的努力と原理の発見」参照）。規則を大前提におく推論では構成的理論に対応できるが、原理的理論には対応できていないのではないか、という疑問である。アインシュタインによれば、構成的理論とは「仮説的な構成要素」を出発点にするものである。これに対して、原理的理論とは「経験的に見出された自然過程の一般的性質」を出発点にするものである。
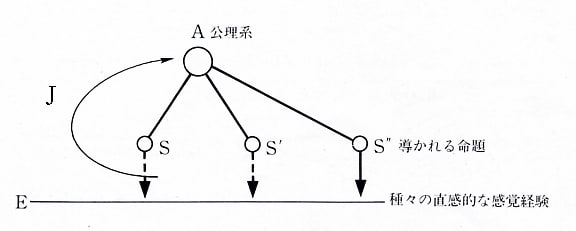
アインシュタインの思考モデルでいえば、原理的理論では最初のE（経験的に見出された自然過程の一般的性質）から、EJASE過程のすべてが問題になる。これに対して、構成的理論では、EJASE過程のすべてが問題になるのではなく、ASE過程が問題になる。出発点とするA（「仮説的な構成要素」）がすでに先行者によって見いだされ存在しているからである。

トーマス・クーンの表現でいえば、構成的理論は「通常科学」(normal science)であり、パースのアブダクションは、「通常科学」の仮説に対応している。それは「パズル解き」としての仮説である。

ここで試みるのは、原理的理論や「異常科学」（extraordinary science）の仮説をつくること（making a hypothesis）である。それはパースとは違ったアブダクションである。

アブダクション異聞1

まず、アブダクションを定式化したときのパースの説明を読んでみよう。
（引用はじめ）『アブダクション』（米盛裕二）参照
わたくしがある部屋に入ってみると、そこにいろいろな違う種類の豆の入った多数の袋があったとする。テーブルの上には手一杯の白い豆がある。そこでちょっと注意してみると、それらの多数の袋のなかに白い豆だけが入った袋が一つあるのに気づく。わたくしはただちに、ありそうなこととして、あるいはおおよその見当として、この手一杯の白い豆はその袋からとり出されたものであろうと推論する。この種の推論は仮説をつくること（making a hypothesis）と呼ばれる。（CP:2.623）
（引用おわり）
部屋の中に、いろいろな違う種類の豆の入った多数の袋があり、テーブルの上には手一杯の白い豆がある。これが推論前にわかっていることである。しかし、袋の中身も、どの袋からとり出されたのかもわからない。不確定なことばかりだが、白い豆の由来を考えるために、パースは1「白い豆だけが入った袋があること」と2「白い豆が1つの袋からとり出されたこと」の２つに可能性を絞る。
パースは、白い豆だけが入った袋が1つあるのに気づき、テーブルの上の白い豆はその袋からとり出されたものだろうと推論する。
すなわち、パースはまず、1「白い豆だけが入った袋があること」に着目する。「多数の袋のなかに白い豆だけが入った袋が一つあるのに気づく」。そして、これを推論の前提として組み入れて（1は大前提とし、テーブル上の白い豆は小前提とする）、そして2「白い豆がその袋からとり出されたこと」を結論として推論する。

(1)この袋の豆はすべて白い（大前提・規則）、
(2)これらの豆は白い（結論・結果）、　　　　　　　　　、
(3)ゆえに、これらの豆はこの袋の豆である（小前提・事例）。

下線の上が推論の前提（大前提と小前提）、下が結論である。命題の後の（）内は演繹での位置づけである。パースのアブダクションは演繹での大前提（規則）と結論（結果）から小前提（事例）を導きだす推論になっている。

次に、このパースの設定している部屋の説明から、パースとは違ったアブダクションの可能性を探ってみよう。

探究の三段階論

『弁証法の系譜』（上山春平著、こぶし書房、2005）をパースに着目して読み直している。「探究の三段階」という表現があることを知った。1905年ころの草稿だという。「私は、いま、探究の三段階における推論過程の正当な根拠に関して、私の到達している結論を述べたいと思う。」
「探究の三段階における推論過程」とは、「アブダクション→ディダクション→インダクション」のことである。パースの最終の定式は次のようなものである。
（引用はじめ）上山が要約したパースの定式をピックアップして引用。
「アブダクション」は、探究の第1段階であり、仮説形成（新しい理論の発見、新しい着想）の過程である。この過程は、現象の観察を起点とし、仮説の発見をへて、仮説の定立におわる。
「ディダクション」は探究の第2段階であり、「アブダクション」の提供する仮説をテストするために、それを論理的推論の前提にくみかえ、そこからあらゆる可能な結論をひきだす過程である。
「インダクション」は、探究の第3段階であり、「アブダクション」の提供する仮説から、「ディダクション」によってひきだされた可能な論理的結論を、事実とつきあわせて、仮説の真理性を確証する過程である。
（引用おわり）
この探究の三段階論はアインシュタインの思考モデルと対応すると想定しているものである。ホルトンはアインシュタインの思考モデルを「EJASE過程」と呼んだが、仮説が確証されることに着目すれば、最後にAを追加して「EJASEA過程」と呼ぶのもよいだろう。このように見ると、探究の三段階と思考モデルは次のような対応になる。思考モデルでは、Aは「公理」となっているが、ここでは「仮説」と考えている。

アブダクション（仮説）　　EJA
ディダクション（演繹）　　AS
インダクション（帰納）　　SEA


単純な対応だが、便利な点は、連結が見やすいことである。仮説Aを段階ごとに確認できる。
このように探究の三段階の定式は受容できるが、パースのアブダクションの定式は、この三段階論においても維持されているのだろうか。疑問としなければならない。

パースのアブダクション（仮説）は、規則と結果から事例を推論するものである。
(1)この袋の豆はすべて白い（規則）、
(2)これらの豆は白い（結果）、
(3)ゆえに、これらの豆はこの袋の豆である（事例）。
これに対して、ディダクション（演繹）は、規則と事例から結果を推論するものである。
(1)この袋の豆はすべて白い（規則）、
(2) これらの豆はこの袋の豆である（事例）、
(3)ゆえに、これらの豆は白い（結果）。
この1アブダクションと2ディダクションをつないでみよう。

1規則・結果・事例――2規則・事例・結果。

三段階論のアブダクションは仮説の形成であり、この仮説はディダクションの出発点となっている。それは「規則」に対応するはずである。しかし、パースの定式の第3項目は「事例」になっていて、ディダクションの第1項「規則」とつながっていない。

パースのアブダクションの定式に立ち入ってみよう。

思考モデルと探究モデル

ホルトンは、アインシュタインの思考モデルを、科学理論の形成にたいするEJASE過程と呼んでいる。


以前、EJA過程に着目して、ここに伊東俊太郎の「発見的思考」を重ねてみた。この対応は拡張できるのではないか。

EJA　 アブダクション（仮説）
AS　　ディダクション（演繹）
SE　　インダクション（帰納）

いいかえれば、アインシュタインの思考モデルとパース探究モデルは対応する。
上山春平によるとパース探究過程は次のようである。（『弁証法の系譜』より）
（引用はじめ）
パースの論理思想の基本的性質は、つぎの言葉に要約されている。「アブダクションは、仮説を形成する過程であり、……ディダクションはヒントにもとづいて予見をひきだし、インダクションは、この予見をテストする」。パースによれば、≪アブダクション≫とは、現象の観察を出発点とし、仮説の発見をへて、仮説の定立にいたる仮説形成（新しい着想、新しい理論の発見）の過程、≪ディダクション≫とは、≪アブダクション≫の提供する仮説を論理的推論の前提命題に組みかえ、そこから論理的に可能な結論をひきだす過程、≪インダクション≫とは、≪ディダクション≫によってひきだされた論理的結論を、事実とつきあわせることによって、≪アブダクション≫によって提供された仮説の真偽（真理性）を検証する過程をさす。
（引用おわり）

楕円の発見と周期律の発見

ハンソンは『科学的発見のパターン』で、「ケプラーの仕事は、ティコのデータを基にしたとき、それらのデータのすべてを包含してくれるもっとも簡単な曲線は何であろうか、という問題だった」と述べている。このハンソンの指摘を見て、『科学的発見のパターン』の「パターン」は、伊東俊太郎の「システム化」と対応するのではないかと思った（「科学的発見の論理」『科学と歴史』所収）。
伊東俊太郎は「発見的思考」を、Ａ帰納（induction）によるもの・Ｂ演繹（deduction）によるもの・Ｃ発想（abduction）によるものの三つの思考方式に大きく分け、「Ｃ発想」のなかを、さらに１類推によるもの・２普遍化によるもの・３極限化によるもの・４システム化によるものと細分している（注）。
「システム化によるもの」とは、「多くの事実を、ある観点から１つのシステムとして関係づけ、そこに法則を発見するものである。」
例えば、同じ要素・同じデータの集まり（第１図）に対して、観点によって、さまざまにシステム化できる（第2,４,5図）。

「同じものを見ていながら、そこに新たに観点を導入することにより、それらを異なったパターンないし関係において捉え直すことがシステム化による発見である。」
伊東俊太郎は、メンデレーエフによる元素の「周期律」の発見をシステム化の例として挙げている。わたしは、ケプラーの「楕円軌道」の発見を追加したいと思う。
「ティコのデータを基にしたとき、それらのデータのすべてを包含してくれるもっとも簡単な曲線」は、円でもなく卵形でもなく楕円だった。
ニュートン力学の形成過程と周期律の形成過程にはいろいろ興味深い対応があるが、ケプラーの楕円の発見とメンデレーエフの周期律の発見が同じ「システム化」というのは特に興味深い。

（注）

発見的思考の分類 (伊東俊太郎「科学的発見の論理」より)

発見的思考		例
Ａ帰納		ボイルの法則、スネルの法則
Ｂ演繹		ニュートンの逆自乗の法則
Ｃ発想	１類推	ダーウィンの自然選択説、ドゥ・ブロイの波動力学
	２普遍化	ニュートン力学、アインシュタインの相対性理論
	３極限化	ガリレイの｢慣性の法則｣・｢自由落下の第一法則｣
	４システム化	メンデレーエフの周期律

中山正和の仮説設定

中山正和は『演繹・帰納・仮説設定』（産業能率大学出版部、1979年）において、パースがアブダクション（仮説設定）を演繹と帰納から分離し、独立させていることを高く評価している。しかし、パースがアブダクションを帰納（インダクション）と同じように拡張的推論と捉えていることには批判的である。拡張という契機に対してではなく、推論そのものに対してである。推論は「理性的なものでコトバによる」ものだが、仮説設定（アブダクション）は「コトバ」によらないもので推論ではないと主張している。「仮説」は「直観」によって気づかれるのであって、「推論」によって選ばれるものではないというのが中山正和の立場である。これはもちろんパースのアブダクションの否定である。

中山正和のアブダクション（仮説設定）の位置づけをみておこう。
中山にとって推論は、演繹と帰納の２つだけで、仮説設定を推論から切り離し直観として独立させる。もちろん、仮説設定は演繹と帰納と無関係ではなく、次のような関係が想定されている。
（引用はじめ）
このように考えてくると、私にはこの、演繹、帰納、仮説設定が、つぎのように「弁証法的構造」に見えてくるのである。

（正）（反）　帰納
　　　　　　　↓↑　　→（合）仮説設定　
（反）（正）　演繹

すなわち、問題が解けないというのは、自分の知っている法則から演繹的に推論したことと、自分が観測した事実から帰納的に推論したことが対立・矛盾している状態であろう。簡単にいうと「リクツはそうだが事実は違う」ということだ。これはいずれを「正」「反」としてもいいが、とにかく対立・矛盾する。これに対しての「合」が仮説設定であって、あることにハッと気づけば、この対立・矛盾は解消（止揚）されるのである。
（引用おわり）
「リクツはそうだが事実は違う」というのは、「驚くべき事実Cが観察される」（パース）、「常識からはふに落ちないようなある現象Pが観測される」（ハンソン）同じ出発点である。パースはここから次の演繹（ディダクション）・帰納（インダクション）へと繋げていったのに対して、中山はここにとどまり仮説設定の具体的方法に言及していった。
演繹と帰納を止揚する矢印→を「直観」とみるのが中山正和のアブダクション、「推論」とみるのがパースのアブダクションである。矢印→は、はたして、直観なのだろうか、推論なのだろうか。

袋のなかの白い豆2

パースのアブダクションの定式は、仮説を作る推論の定式になっていないのではないだろうか。
パースのアブダクション（仮説）は次のようだった。

(1)この袋の豆はすべて白い（規則）、
(2)これらの豆は白い（結果）、
(3)ゆえに、これらの豆はこの袋の豆である（事例）。

アブダクション（仮説）は帰納と同じような拡張的推論である。それならば、(3)に来るのは「この袋の豆はすべて白い」（規則）だろう。これは帰納の(3)と同じである。
(1)に来るのは、帰納の(1)「これらの豆はこの袋の豆である」（事例）のような袋に入った豆ではなく、裸の白い豆だろう。「これらの豆は白い（結果）」。
(2)に来るのは、残りの「これらの豆はこの袋の豆である」（事例）である。

整理すると、アブダクション（作理）は次のようになる。

(1)これらの豆は白い（結果）
(2)これらの豆はこの袋の豆である（事例）、
(3)ゆえに、この袋の豆はすべて白い（規則）。

この定式の方が、アブダクションの推論形式と相性がいいのではないか。

(1)驚くべき事実Cが観察される、
(2)しかしもしHが真であれば、Cは当然の事柄であろう、
(3)よって、Hが真であると考えるべき理由がある。

記号で表記すると、
　　　(1)C
　　　(2)H→C
　　　(3)H

（注）
演繹
(1)この袋の豆はすべて白い（規則）、
(2)これらの豆はこの袋の豆である（事例）、
(3)ゆえに、これらの豆は白い（結果）。
帰納
(1)これらの豆はこの袋の豆である（事例）、
(2)これらの豆は白い（結果）、
(3)ゆえに、この袋の豆はすべて白い（規則）。

『アブダクション』（米盛裕二著、勁草書房、2007）参照

アブダクションの推論形式

アブダクションの推論の形式を確認しておこう。
パース（1839～1914）、ハンソン（1924～1967）、ポリア（1887～1985）の順。

パース　『アブダクション』（米盛裕二著）より

驚くべき事実Cが観察される、
しかしもしHが真であれば、Cは当然の事柄であろう、
よって、Hが真であると考えるべき理由がある。

アブダクションは、「リトロダクション（遡及推論）」とも呼ばれている。

ハンソン　『科学的発見のパターン』（ハンソン著、村上陽一郎訳）より　

(1)常識からはふに落ちないようなある現象Pが観測される。
(2)Pは、もしHが正しいとすれば、Hによって当然のこととして説明しうるものとなる。
(3)それゆえHが正しいと考えるにはそれだけの理由がある。

記号で表記すると、
　　　P
　　　H→P
　　　H
これは「仮説提起の推論」（伊東俊太郎）と呼ばれている。

ポリア『いかにして問題をとくか』（ポリア著、柿内賢信訳）より

AならばBである。
Bは正しい。　　　　　　　　　。
Aは正しいということは確からしい。

これは「発見的三段論法」（Heuristic syllogism）と呼ばれている。
この結論には次のような注釈が付いている。「発見的三段論法の結論は、その前提と論理的性格を異にしていて、もっとぼんやりした、明確でない、不完全な表現である。この結論は力と同じように方向と大きさをもっている。すなわちそれによってAがもっと信ずべきものになるという方向を示している。それと同時に大きさを示す。Aは甚だ信ずべきものであるとか、ほんの少し信ずべきであるとかのようである。」

袋のなかの白い豆

下はパースのアブダクションの説明である。『アブダクション』（米盛裕二著、勁草書房、2007）参照。
（引用はじめ）
わたくしがある部屋に入ってみると、そこにいろいろな違う種類の豆の入った多数の袋があったとする。テーブルの上には手一杯の白い豆がある。そこでちょっと注意してみると、それらの多数の袋のなかに白い豆だけが入った袋が一つあることに気づく。わたくしはただちに、ありそうなこととして、あるいはおおよその見当として、この手一杯の白い豆はその袋からとり出されたものであろうと推論する。この種の推論は仮説をつくること(making a hypothesis)と呼ばれる。
（引用おわり）
この推論は次のように定式化されている。
アブダクション（仮説）
(1)この袋の豆はすべて白い（規則）、
(2)これらの豆は白い（結果）、
(3)ゆえに、これらの豆はこの袋の豆である（事例）。

規則、結果、事例は三段論法の大前提、結論、小前提に対応しているが、はたして、これは「仮説をつくる(making a hypothesis)」推論の説明になっているのだろうか。なっているような気もする、なっていないような気もする。

（注）
演繹と帰納は次のようである。
演繹
(1)この袋の豆はすべて白い（規則）、
(2) これらの豆はこの袋の豆である（事例）、
(3)ゆえに、これらの豆は白い（結果）。
帰納
(1) これらの豆はこの袋の豆である（事例）、
(2) これらの豆は白い（結果）、
(3)ゆえに、この袋の豆はすべて白い（規則）。

『アブダクション』（米盛裕二著）参照

｢直観｣と｢アブダクション｣

ポオ（1809～1849）の「直観」はパース（1839～1914）の「アブダクション」の先駆けではないかと思う。ポオは『ユリイカ』（1848年）の導入部で、アリストテレスの演繹法とベーコンの帰納法に疑問を投げかけている。そして、この二つとは違う第三の方法を想定している。それをポオは「直観」と呼んでいるが、むしろ新しい推論として「アブダクション」の萌芽とみたほうがいいのではないか。
（引用はじめ）
直観とは「帰納ないし演繹に由来するものだが、その過程が影のごとく判然としないので、我々の意識にのぼらず、われわれの理性をすり抜け、われわれの表現能力をうわまわるところの確信に他ならない」（八木敏男訳、岩波文庫、2008）
（引用おわり）
ポオは「直観」によって得た「仮定」を起点にして宇宙論を展開するが、ケプラーの三法則も「直観」によって導かれたと考えている。
（引用はじめ）
ケプラーはかの重要な三法則を憶測した――つまり想像したのです。それに到達した道筋が演繹法であったか帰納法であったかと、もしケプラーが問われたとしたら、さだめしこう答えたでありましょう――「わしは道筋のことは何も知らん――だが、わしは宇宙のからくりを知っている。これがそうだ。わしはそれを自分の魂でつかんだのだ――ただ直観だけを頼りにそこに到達したのだ」と。
（引用おわり）