鶴見俊輔のアブダクション

書庫に鶴見俊輔著『アメリカ哲学（上）』（講談社学術文庫、1976）があった。読んだ形跡があった。最初の3章はパースが取り上げけられていた。記憶になかったが、アブダクションにも言及があった。abduction（アブダクション）は「構想」と訳されている。

プラグマティズムの最初の格言（1878）が最も重要なものとして分析されている。それは「いくつもの” conceive”が最後に一括されて、”consider”に包まれている」という構造をもっている。これは、一時的に発想（conceive）された考えを持続的に熟慮（consider）して包摂する構造を示している。このようなconceiveとconsiderの関係は、探究の第1段階（アブダクション）の構造と対応しているように思われる。

思考モデルと拡張的推論

アインシュタインの思考モデルにおいて、本質的に論理的なものではないと指摘されているのは、AとEとの関係、SとEとの関係である。もちろん確実性の違いはあり、SとEとの関係の方が、AとEとの関係より確かなものである。

（引用はじめ）
(4)ＳはＥと関係づけられる（つまり経験によってテストされる）。この過程もまた論理のほかの（直感的）領域に属する。というのもＳに現れる概念と直接経験Ｅとの間の関連は、本質的に論理的なものではないからである。/しかし、このＳとＥの間の関係は実際のところＡのＥに対する関係に比べれば、はるかに確かなものである。
（引用おわり）
本質的に論理的にものではないというのは、パースの拡張的推論と対応している。また、確実性の違いは、「帰納は仮説よりもいっそう強力な種類の推論である」（パース）に対応している。AとEとの関係はアブダクション、SとEとの関係はインダクション（帰納）である。

アインダクション2

パースは「直観」を「以前の認識によって限定されない認識」すなわち「意識の外にある事物によって限定される認識」という意味で用いている（パース「論文集」（『世界の名著48』所収））。そして、認識はすべて以前の認識によって限定されるものであって、「直観」の存在を否定している。いいかえればすべては推論だと主張している。このような姿勢はアインシュタインの思考モデルとまったく重ならない。というのは、アインシュタインはEJAの過程を、直観（直感）的なつながりがあるだけで、論理的なつながりはないと特徴づけているからである。「心理学的にはＡはＥに依存している。しかし我々をＥからＡに導く論理的経路は存在しない。そこにはただ直感的（心理的）なつながりがあるだけである」。
（注1）

しかし、パースの「探究モデル」の第一段階、アブダクションの説明では、直観（直感）を容認する姿勢を示しているようにみえる。
（引用はじめ）（上山春平著『弁証法の系譜』）
この過程（アブダクションのこと、注）は、(1)現象の観察を起点とし、(2)仮説の発見をへて、(3)仮説の定立におわる。（この過程は形式化できない。そうした推論過程をパースは”Argument”とよび、形式化のできる”Argumentation”と区別する）。
(1)あらゆる研究は、不可解な現象を、いろいろな側面から観察し、考察することからはじまる。その目標はこうした現象の謎を解くための説明もしくは仮説を見つけることである。(2)われわれは、観察をかさねるうちに、そうした仮説を突然思いつく。(3)しかし、この仮説のうけいれ方には、たぶんこんなことではなかろうかといったはなはだ消極的な態度から、どうしてもそれを信じないではいられないというきわめて積極的な態度にいたるまで、無数の段階がある。
（引用おわり）

反対に、アインシュタインは「理論物理学の方法について」（選集３所収）では推論を容認する姿勢を示している。（注2）
（引用はじめ）
理性は体系の構成を与え、種々の経験内容とそれらの相互関係は理論から結論される諸命題の中にそれらの表現を求めなければなりません。全体系の、とりわけその体系の基礎をなしている概念および基本法則の価値と正当性は、この種の表現が可能かどうかということにもっぱらかかっています。
（引用おわり）
パースとアインシュタインは違った表現をしているときがあるが、同じ過程を見ているのだと思う。

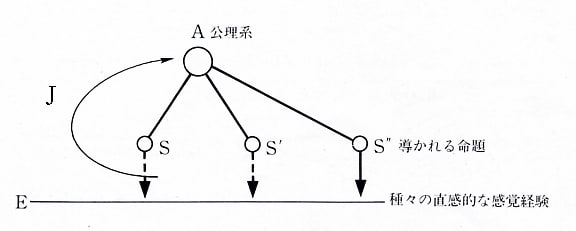
（注1）
この図は「アインシュタインロマン」からのものだが、Jはホルトンの説明に合わせて、追加している。また、S^”からEへの矢印が実線になっているのは、アインシュタインのスケッチを忠実に再現しているものである。しかし、これはSやS^’と同じように破線で描くはずだったが、インクがひろがって実線になってしまったものだろう。実際、ホルトンの図では、S^”も破線で描かれている。
（注2）
ホルトンは「科学理論の形成に関するアインシュタインのモデル」で、この箇所にもとづいて次のように指摘している。
（引用はじめ）
もともと根本的仮定Aを想定する段階でさえ、彼はインスピレーション的要素が欠かせないと主張しながらも、公理の「体系に構造を与えるのは理性の仕事である」という。
（引用おわり）

演繹/帰納とphilosophy

演繹と帰納は、deductionと inductionを西周が翻訳したものである。duction（導）に対してde（出）とin（入）で、対照的に翻訳すれば、導出と導入である。演繹と帰納では関連がわかりづらいと思っていたが、これは漢字に対する知識がないことに起因しているのではないかと思うようになった。演繹と帰納を分析してみると、「演」「繹」は、「引き出す」の同義語、「帰」「納」は「納める」の同義語である。「導」は方向を指していると考えれば、同義語を繰り返すことによって、演繹は出す方向、帰納は入れる方向を指している。これは、語源を踏まえた忠実な翻訳のように思える。

呉智英はdeductionと inductionに対して、出理、入理を提案した。わたしは演繹より出理、帰納より入理のほうがわかりやすいと思う。しかし、語源自体に「理」は欠如しているのではないかと思う。語源では「何」から出すのか、「何」に入れるのかは問題になっていない。
deductionと inductionは方向だけを示していて、philosophyのような構造（philo-「希（こいねがう）」、sophia「知」、希哲学）を示していないのである。

「理」を補足し同義語を追加して、演繹から入理、帰納から出理を導いてみよう。

演繹→演繹理→演出理→出理
帰納→帰納理→納入理→入理

帰納とアブダクション

米盛裕二はポリアの発見的推論（「発見的三段論法」）がパースのアブダクションの形式と同じであることを指摘している（『アブダクション』）。しかし、ポリアが「帰納的推論」に留まり、帰納とは異なる「重要な方法的特性を見落としている」のではないかと疑問を呈している。

ポリアの発見的論理（「発見的三段論法」）に対する自身の位置づけは次のようなものである。『いかにして問題をとくか』(How to Solve It)
（引用はじめ）
「〈発見的推論〉とか、〈帰納的推論〉あるいは（すでに存在する言葉の意味を拡張することを好まなければ）〈そうらしいという考え方〉と呼ぶことができる。ここでは最後の呼び方を採用する。」（柿内賢信訳）
(We could call the reasoning that underline this kind of evidence) “heuristic reasoning” or “inductive reasoning” or (if we wish to avoid stretching the meaning of existing terms) “plausible reasoning.” We accept here the last term.(G.Polya)
（引用おわり）
これに対する米盛裕二の疑問は次のようなものである。
（引用はじめ）
ここでポリアが「そうらしいという考え方」という呼び方をしているのははなはだ曖昧で、それは発見的推論が普通の帰納よりも弱い蓋然的推論であるということを意味しているようにもとれますが、しかしその蓋然的推論が帰納的推論なのか、それとも帰納とは違う別の種類の蓋然的推論なのかは明確ではありません。
（引用おわり）
ポリアは『いかにして問題をとくか』では「そうらしいという考え方」と言っているが、『発見的推論そのパターン』（数学における発見はいかになされるか２、PATTERNS OF PLAUSIBLE INFERENCE、Mathematics and Plausible Reasoning 2 ）では「帰納的パターン」と言っている。
（引用はじめ）（柴垣和三雄訳）
（前略）つぎのような蓋然的推論の一つのパターンがある。
AはBを含蓄する
Bは真である　・
Aは信頼が増す
（If A then B
　B true　　　　・
　A more credible）
この型を基本的な帰納的パターン、あるいは幾らか簡潔に「帰納的パターン」と呼ぼう。
この帰納的パターンは別に驚くべきことをいってはいない。反対に、それは理性的な人なら疑うとは思えない信念: 結果の確証は推測の信頼性を増す、ことをいい表わしている。少し注意すれば、日常生活において、法廷において、科学において、等々、このパターンに従うと思われる推論は数限りなく見られるのである。
（引用おわり）
米盛と同じように、わたしにもポリアの発見的三段論法はパースのアブダクションの形式と同じだと思える。しかし、それは米盛と違って、「帰納とは違う別の種類の蓋然的推論」であるのは明確であるようにみえる。
米盛裕二のポリアへの疑問はパースのアブダクションを絶対視する考え方からみちびかれているのではないだろうか。わたしには、ポリアの「帰納的パターン」はパースのアブダクションを「帰納」の側面から見直す契機を示しているのではないかと思われる。

帰納の分割

米盛裕二によれば、パースの帰納は３つに分かれる（『アブダクション』）。観察された事例の一般化（単純・量）と探究の過程での役割（質）に着目したものである。
1 単純帰納…「単純枚挙による帰納法」（ベーコン）
2 量的帰納…数学的確率論にもとづく帰納
3 質的帰納…仮説を実験的にテストし検証する方法
アインシュタインの思考モデルに位置づけている帰納は3の質的帰納である（SEA）。1と2は帰納が「仮説」が前提になっていることに基づいてEJA（アブダクション）に入れることになる。

アインダクション

Einduction（アインダクション）は、Einsteinと３つのduction（ deduction/ induction/ abduction 演繹/帰納/仮説）を統一するものである。これは、わたしの造語で、カテゴリー「アブダクション」の理念である。
Einsteinは、アインシュタインの思考モデル（EJASE過程、ホルトン）を指している。


他方、３つのdutionはパースの「探究の論理学」（探究の３段階論）である。
「アブダクションは、仮説を形成する過程であり、……ディダクションはヒントにもとづいて予見をひきだし、インダクションは、この予見をテストする」。

Einduction（アインダクション）は、この２つを１つ（ein）の推論の過程として統一する姿勢を示している。出理・入理・作理（注）を１つの究理として統一する。強調して、順序よくかけば、3つの「作」理・「出」理・「入」理を統一して、１つの「究」理として統一する。

（注）
「出理・入理・作理」

アブダクション異聞5

パースのアブダクションを演繹モデルと呼ぶことによって、アブダクションの帰納モデルを展望している。演繹モデルと相性のいいアブダクションの推論形式（注）は、帰納モデルでも成立していると想定しているが、それでよいのだろうか。十分に説明できないでいる。
それで、帰納モデルとして独立させるのではなく、演繹モデルに従属させるモデルも検討している。つまり、大前提となっている規則を推論する前段階として帰納を演繹モデルに内在させてみるのである。

（注）
(1)驚くべき事実Cが観察される、
(2)しかしもしHが真であれば、Cは当然の事柄であろう、
(3)よって、Hが真であると考えるべき理由がある。
記号で表記すると、
(1)C
(2)H→C
(3)H

アブダクション異聞4

パースのアブダクションは規則Ruleを大前提として推論が開始される。ここに着目してパースのアブダクションをアブダクションの演繹モデルと呼んでみよう。これに対して、わたしが想定するアブダクションは規則Ruleを結論とする推論だから、アブダクションの帰納モデルとしよう。
EJA過程は「アブダクション」である。通常は演繹モデルのアブダクションが行われる。これがうまくいかなくなると、演繹モデルは捨てられる。異常なアブダクションに対応できるように帰納モデルが立ち上がる。

アブダクション異聞3

パースと違ったアブダクションの可能性とは、パースの順序と逆の推論である。テーブルの白い豆が、多数の袋の中のある1つの袋からとり出されたことに最初に気づくという想定である。つまり、2「白い豆が1つの袋からとり出されたこと」に気づき、これを前提に組み入れ（テーブルの白い豆は大前提、2は小前提とする）、1「白い豆だけが入った袋があること」を結論として推論する。
パースの説明に重ねてみよう。
「わたしがある部屋に入ってみると、そこにいろいろな違う種類の豆の入った多数の袋があったとする。テーブルの上には手一杯の白い豆がある。そこでちょっと注意してみると、それらの多数の袋のなかの１つの袋から手一杯の白い豆がとり出されたことに気づく。わたしはただちに、ありそうなこととして、あるいはおおよその見当として、その袋のなかの豆はすべて白いだろうと推論する。この種の推論も仮説をつくること（making a hypothesis）と呼ばれる。」
(1)これらの豆は白い（結論・結果Result）、
(2)これらの豆はこの袋の豆である（小前提・事例Case）、
(3)ゆえに、この袋の豆はすべて白い（大前提・規則Rule）。

下線の上が推論の前提（大前提と小前提）、下が結論である。命題の後の（　）内は演繹での位置づけである。このアブダクションは演繹での結論（結果）と小前提（事例）から大前提（規則）を導きだす推論になっている。

この推論は「帰納」と同じ第3格（注1）になっている。媒名辞Mと小名辞S（結論の主語）と大名辞P（結論の述語）は次のように並ぶ。M（これらの豆）、S（この袋の豆）、P（白い）。
　M――P
　M――S
∴ S――P
ただし、帰納では２つの前提（大と小）はいずれも確実だが、ここ（アブダクション）では大前提だけが確実で、小前提は不確実な想像された前提である。
２つの前提（大と小）の前後はパースの帰納（注2）と逆になっている。ここで「これらの豆は白い」（テーブルの上の白い豆）を大前提とするのは、インダクションとしての帰納とアブダクションとしての帰納を区別するためである。また出発点としてのE「経験的に見出された自然過程の一般的性質」との対応を想定していることもある。

（注1）
パースのアブダクションは第2格である。
(1)この袋の豆はすべて白い（大前提・規則Rule）、
(2)これらの豆は白い（結論・結果Result）、
(3)ゆえに、これらの豆はこの袋の豆である（小前提・事例Case）。
媒名辞Mと小名辞S（結論の主語）と大名辞P（結論の述語）が、次のように並んでいる。M（白い）、S（これらの豆）、P（この袋の豆）。
　P――M
　S――M
∴ S――P

ちなみに、ディダクション（演繹）は第１格である。
(1)この袋の豆はすべて白い（大前提・規則Rule）、
(2) これらの豆はこの袋の豆である（小前提・事例Case）、
(3)ゆえに、これらの豆は白い（結論・結果Result）。
媒名辞Mと小名辞S（結論の主語）と大名辞P（結論の述語）は次のように並ぶ。M（この袋の豆）、S（これらの豆）、P（白い）。
　M――P
　S――M
∴ S――P
これは確実な推論である。しかし、第１格だけでなく、第２格や第３格にも推論としての存在理由を認め、探究の論理学を提起するところにパースの試みがあった。（上山春平『弁証法の系譜』参照）

（注2）
パースの帰納は次のようである。
(1)これらの豆はこの袋の豆である（小前提・事例Case）、
(2)これらの豆は白い（結論・結果Result）、
(3)ゆえに、この袋の豆はすべて白い（大前提・規則Rule）。
これはアリストテレスの定義「帰納とは小前提と結論から大前提を導きだす推論である」に対応させたように思われる。（『世界の名著48』参照）