今月8日の記事で「π切断のずらし尺を使った計算では間違った答え
が出ることがある。充分ご注意を。」と言ったようなことを書いた。
これを読んだ方は不安になったであろう。実際わたし自身,不安に駆
られ,その後ずっとこのことに悩み,計算尺の操作にはまり込んでし
まった。「何に注意したらいいのか?」つまり,「どのように計算し
たらいいのか?」指針・公式が欲しいのである。
しかし,正直に言うとまだ結論は得られていない。それでも現段階で
分かったことを記事にするのも無駄ではあるまいと思った次第。(頭
の整理のため。)
今回は π 切断のずらし尺を備えた計算尺のみを取り上げる。尺の区分
名称としては,上から
DF, [ CF, CIF, CI, C ], D
の6つである。ものによっては DI 尺をも備えているが,ここでは取
り上げない。なお,[ ] 内は滑尺(中尺)にある。ちなみに,DF 尺
は上側固定尺(本尺,外尺)に,D 尺は下側固定尺(本尺,外尺)に
ある。
下の写真はわたしが学生時代から使ってきたものである。(正確に言
うと2代目。)

上記6つの尺の記号が左側に刻印されているのがわかるであろう。
なお,上の写真では D(2) × CI(7) = D(14) の計算を示している。2 × 7
はカーソル線に一致しており,答えの 14 は滑尺の左基線の下の D 尺
に示されている。
話は前後するが,わたしはこれまで気楽にずらし尺を使って,計算し
てきた。目外れのとき確かに便利。
今回の調査で,まず手許にある計算尺の操作説明書を2冊調べてみた。
もちろん,ずらし尺を使う個所を重点に。その結果,取り上げている
例題はいずれも問題の発生しないものばかりであった。故意に問題を
避けていると疑いたくなる。
だだし,リコー計算尺のポケット解説書では1箇所だけ注意書きがあ
った。
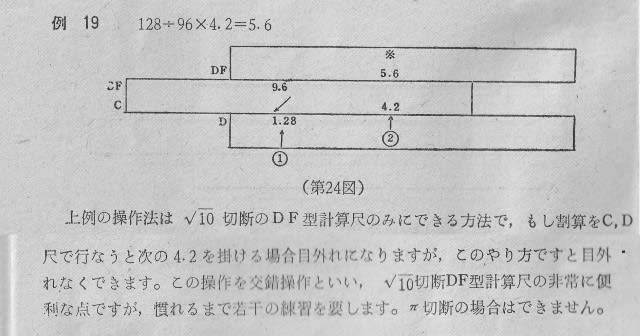
上の写真のとおり,π 切断のずらし尺ではできないと書いてある。
しかし,そのように書いているだけで,どういう場合が駄目なのかは
っきりしない。さらに,「交錯操作」という用語が出てくるが,納得
できる説明がない。
そこで,2×7×8=112 を例題として可能な限りの方法で解いてみた。
その結果を下の表に示す。(表中〇で囲まれたCはカーソル線を示す。)
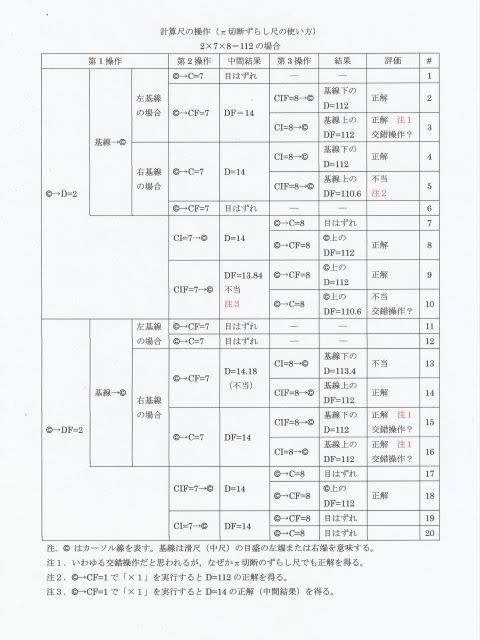
ちょっと見にくいだろうが,20 とおりの計算結果である。本来は
2×3×2×2=24
とおりあるはずだが,目外れのため後続の計算ができない場合があっ
て 20 とおりに減っている。
結果としては9とおりの手順で正解が得られた。( 9 / 20 ) × 100 = 45%
の正答率である。目外れのため計算できなかった場合を除くと,
( 9 / 12 ) × 100 = 75%の正答率となる。
ただし,今回は可能な限りの手順について調べたもので,通常は思い
つかない手順も含まれていることにご留意いただきたい。このような
手順を差し引くと正答率はもっと高くなる。しかし,100%ではない。
表の中をいくつか見てみよう。
まず,#3の場合:
交錯操作と思える手順で正解を得ている。ただし,前述のとおり交錯
操作そのものの定義がはっきりしない。
#9の場合:
2×7の中間結果が正しくないのに最終結果が正しく得られている。
π切断の問題はこのあたりに潜んでいそう。#14の場合も同様。
#9の手順について代数的に解析してみよう。(前回の記事で示した
結果を援用する。)
D × CIF × CF → D(答え):
log ( D × CIF × π**2/10 ) + ( log CF-log 10π )-log π
= log ( D × CIF × π**2 × CF × 10 / π**2 )
= log ( D × CIF × CF )
となって3数の積が真数として得られる。
ところで,何も考えずに上の計算をするとしたら,どの手順になるで
あろうか?わたしの場合間違いなく#8を採る。正解である。
引き続き調べるつもり。
以上
参考資料
①ヘンミNo.255-D計算尺使用法説明書,ヘンミ計算尺(株),1963年(?)
②リコー計算尺ポケット解説書,リコー計器(株),1963年改訂5版
が出ることがある。充分ご注意を。」と言ったようなことを書いた。
これを読んだ方は不安になったであろう。実際わたし自身,不安に駆
られ,その後ずっとこのことに悩み,計算尺の操作にはまり込んでし
まった。「何に注意したらいいのか?」つまり,「どのように計算し
たらいいのか?」指針・公式が欲しいのである。
しかし,正直に言うとまだ結論は得られていない。それでも現段階で
分かったことを記事にするのも無駄ではあるまいと思った次第。(頭
の整理のため。)
今回は π 切断のずらし尺を備えた計算尺のみを取り上げる。尺の区分
名称としては,上から
DF, [ CF, CIF, CI, C ], D
の6つである。ものによっては DI 尺をも備えているが,ここでは取
り上げない。なお,[ ] 内は滑尺(中尺)にある。ちなみに,DF 尺
は上側固定尺(本尺,外尺)に,D 尺は下側固定尺(本尺,外尺)に
ある。
下の写真はわたしが学生時代から使ってきたものである。(正確に言
うと2代目。)

上記6つの尺の記号が左側に刻印されているのがわかるであろう。
なお,上の写真では D(2) × CI(7) = D(14) の計算を示している。2 × 7
はカーソル線に一致しており,答えの 14 は滑尺の左基線の下の D 尺
に示されている。
話は前後するが,わたしはこれまで気楽にずらし尺を使って,計算し
てきた。目外れのとき確かに便利。
今回の調査で,まず手許にある計算尺の操作説明書を2冊調べてみた。
もちろん,ずらし尺を使う個所を重点に。その結果,取り上げている
例題はいずれも問題の発生しないものばかりであった。故意に問題を
避けていると疑いたくなる。
だだし,リコー計算尺のポケット解説書では1箇所だけ注意書きがあ
った。

上の写真のとおり,π 切断のずらし尺ではできないと書いてある。
しかし,そのように書いているだけで,どういう場合が駄目なのかは
っきりしない。さらに,「交錯操作」という用語が出てくるが,納得
できる説明がない。
そこで,2×7×8=112 を例題として可能な限りの方法で解いてみた。
その結果を下の表に示す。(表中〇で囲まれたCはカーソル線を示す。)

ちょっと見にくいだろうが,20 とおりの計算結果である。本来は
2×3×2×2=24
とおりあるはずだが,目外れのため後続の計算ができない場合があっ
て 20 とおりに減っている。
結果としては9とおりの手順で正解が得られた。( 9 / 20 ) × 100 = 45%
の正答率である。目外れのため計算できなかった場合を除くと,
( 9 / 12 ) × 100 = 75%の正答率となる。
ただし,今回は可能な限りの手順について調べたもので,通常は思い
つかない手順も含まれていることにご留意いただきたい。このような
手順を差し引くと正答率はもっと高くなる。しかし,100%ではない。
表の中をいくつか見てみよう。
まず,#3の場合:
交錯操作と思える手順で正解を得ている。ただし,前述のとおり交錯
操作そのものの定義がはっきりしない。
#9の場合:
2×7の中間結果が正しくないのに最終結果が正しく得られている。
π切断の問題はこのあたりに潜んでいそう。#14の場合も同様。
#9の手順について代数的に解析してみよう。(前回の記事で示した
結果を援用する。)
D × CIF × CF → D(答え):
log ( D × CIF × π**2/10 ) + ( log CF-log 10π )-log π
= log ( D × CIF × π**2 × CF × 10 / π**2 )
= log ( D × CIF × CF )
となって3数の積が真数として得られる。
ところで,何も考えずに上の計算をするとしたら,どの手順になるで
あろうか?わたしの場合間違いなく#8を採る。正解である。
引き続き調べるつもり。
以上
参考資料
①ヘンミNo.255-D計算尺使用法説明書,ヘンミ計算尺(株),1963年(?)
②リコー計算尺ポケット解説書,リコー計器(株),1963年改訂5版









