小学生の子たち(主に1~3年生の子らです)と算数を学んでいるときの様子を
いくつか紹介します。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
<帯分数や分母の異なる分数が分かるようになる『分数ゲーム』

小学1年生の子らと分数ゲームを作りをしました。
紙皿を2つに切り分けたもの、3つに切り分けたもの、4つに切り分けたものを
数枚分ずつ作って、ケーキやピザの絵を描いたらできあがり。
サイコロにシールを貼って、2と3と4の数字を書きます。
(サイコロを加工するのがめんどうな時は、普通のサイコロのままで遊んで、
2と3と4以外が目が出た時に振りなおすのでもOKです)

<遊び方>
サイコロを振って、3が出たら3分の1のピース、
2が出たら2分の1のピースを取っていき、
1枚のケーキ(ピザ)を作った方が勝ちです。
勝った人は、1と2分の1のカードを手にして、
1と2分の1を目指してゲームを続けます。
写真では、勝った子が2を目標にしてゲームを続けているところです。

帯分数は習ったときに、できるようになっていても、
しばらくすると、どうやって仮分数に直すのか忘れてしまう子が多いです。
こうしたゲームをしていると、
直観的に2分の1+4分の2=1といった
計算がわかるようになってきます。
また分数の理解が進み、分数のたし算、ひき算、かけ算、割り算などが
できるようになっていきます。
-------------------------------------------------------------------------------------------
<表に整理すること と 規則を見つけだすこと>

小学2、3年生の科学クラブのレッスンで。
メンバーのひとりの☆ちゃんが、「お家でしたけれどわからなかった」という問題を
持ってきてくれました。
小学2年生用の問題集(『スーパーエリート問題集』)に載っているものだとはいえ、
東京学芸大附世田谷中の入試に出た過去問でなかなか難しい規則性の問題でした。
ちょうど科学クラブの子たちは、実験のデーターを表に整理することや、
表から規則的なルールを読みとることを大切にレッスンをしていますから、
実験後の学習タイムにみんなで取り組んでみることにしました。
まず、大きな紙に図を描きなおして、並んでいる奇数に番号を打ちました。

それぞれの番号にある数を書き込んでから、
どのように数が変化しているのか、その数を求めるためにはどんな式を作ればいいのか
アイデアを出し合いました。

科学クラブの子らはどの子もこうしたルールを見つけだすのがとても得意なので、
「できるからやらせて!」「ぼくがやりたい!」「わたしが!」と難なく
書き込んでいました。
が、わたしがいじわるにいきなり、「それなら、100番目はどう?」と
たずねると、1+2×(100-1)のところを、1+2×(101-1)と
間違えていました。数が大きくなるというだけで、何となくこんがらがりますね。

その後、1列目、2列目、3列目それぞれの一番最初の数につけた番号を調べて、
その番号の求め方の規則についても考えました。

↑ ■くんは、30列目の1番最初の数についている番号を
当てることができてうれしそうでした。
答えは、1+2+3+4+5………+29+1
で求まります。

プログラムロボットで遊んでいます。(左端の円柱形のおもちゃです)
一度壊れてから、子どもたちが線をつなぎなおしているので、元の形と異なります。
ロボットで紙コップを倒すコースを作っていたのですが、良い写真が残っていません。

■くんがブロックで作ったゲームで■くんと☆ちゃんが遊んでいたのですが、
「ルール違反をした」とか「こんな小さなスペースで試合の仕様がない」とか
「そんなルール聞いていない」とか「サッカーでの罰則は、このゲームでも
あたり前に守るべき」とかでひと揉め。
そこへ●くんが、「何揉めてるの?」と仲裁に入り、
どうすれば解決するかいっしょに考えてあげていました。

ルールをもう一度確認しあい、ゲームのサイズを大きく作りなおして
一件落着です。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
<2年生の子らと規則性>

小学2年生の女の子たちのレッスンで。
数ヶ月前から算数の力がしっかりついてきた女の子ふたり。
文章題なら最レベの3年生の複雑な問題もスムーズに解けるようです。
ひとりの子が、「でも、これはさーっぱりわからなかった」と言いながら持ってきて
くれたのが、中学入試用の規則性の問題が載っている問題集です。
三角形が積み重ねてあって、「三角形が81枚になるときは、何段目の時か?」
といった問題です。
こうした規則性の問題は確かに難しいけれど、一方ではいくつの子がチャレンジしても、
パズルやゲームに似た解く楽しさを満喫できる問題だとも言えるのです。
足し算さえできたら、後は紙に書きだしていく方法さえ工夫すれば
答えにたどりつけるのですから。
そういえば、息子が
「難問を解くということは、汎用性の高い基礎的な事柄をしっかり身につけること
でもあるよ」とつぶやいていたのを思いだしました。
こうも言っていました。
「難しい問題を解いても意味がない、易しい問題をたくさん解くべきだって言う人は
多いけどね。でも東大や京大の数学の問題のように難解だと思われている問題は、
実際には、数の世界の基本中の基本を扱っているというか、
数学のそれぞれの問題の本質的な意味を理解しているかどうかを問うているところが
あるよ。だから、センターの問題は小学生に解かせても意味がないけれど、
東大の問題なら小学生の解かせてみたたら楽しめるんじゃないかって問題
がけっこうあるよ。
体系的な知識の積み重ねや訓練で解くのではなく
直観的な洞察力を使って解くものが主だから。遊びの要素が濃いのかな。
といっても、しっかり解けるようになっておくには、勘だけじゃ無理で
時間はいるな。ある程度の時間、それに関わるのは避けられないけど。
もうちょっと時間が欲しいな」
超のんびり屋の息子も、受験日が近づくとさすがに時間の大切さを
実感している模様です。
話を2年生の子らのレッスンに戻しますね。
規則性の問題を理解するために
ブロックで規則的に大きくなっていく形を作りました。
最初は小さなサイズで作るつもりが、女の子ふたりとも、どんどん三角を大きく
することが楽しくてたまらなくなって巨大な三角形をこしらえていました。
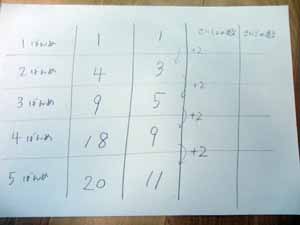
表を作って気づいたことやわかったことを話しあうと
どんどん面白い意見が出ました。
ブロックのパーツのひとつひとつに上から番号をつけていくと、(左から右)
3段目なら、5,6,7,8、9の番号になります。
そのように番号をつけていく時、4段目の一番小さな数はいくつで、
一番大きな数はいくつか、10段目の一番小さな数はいくつで、
一番大きな数はいくつかといった問題も考えました。
ブロックでさんざん遊んでいた子らは、ブロックを指さしながら、
「一番小さい数って前の段の最後の数よりひとつ大きくなるだけだから
そんなの簡単だ」と言っていました。

↑ 自分なりに数のきまりについて書いて考えいました。

規則性の問題を子どもと楽しみたいという方は
写真のようなブロックの山を作りながら、
「この三角の山に隠れている秘密を探り出そう!」と提案して、
思いつく限りのルールを自由に言い合うといいかもしれません。
規則性の問題の解き方を教えるのではなくて、物をよく観察して、
「いくつずつ増えているか」とか「こういう表を作ってみたら面白そう」といった
自由なアイデアを出しあって紙に書いて検証しあうのです。
計算してみて、面白いルールを見つけたらそれも発表しあいます。
算数の世界がとても好きになりますよ。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
<どうして低学年の子に植木算や旅人算などを教えているの?>
虹色教室では、小学校低学年の子らにも
植木算や旅人算といった中学入試向けの算数の問題に触れる機会を
たくさん設けています。
でも「どうして?いくら何でもそんな先取り必要なの?」と感じている
方がいらっしゃるかもしれませんね。
実際に、とても有利にはなるでしょうが、
中学入試に有利だから、という理由でそんなことをしているわけではありません。
さまざまな理由がありますが、
一番の理由は、算数が実生活でどのように役立つのか、
今練習している計算訓練は、何のためにあるのか、
問題を通じて自然に理解することができるからなのです。
算数の本当の面白さや頭を使うことの楽しさにも気づけます。
植木を道路に植えていくということ、
自分が見慣れている都市の景観にどれほど算数が深くかかわっているのか、
そうしたことを知っていると、「算数が将来なんの役に立つんだ?」
何て疑問に縛られて、やる気を失うこともありませんよね。
野球の試合も見せずに、野球を知らない子に、素振りばかり練習させても、
上達させるのは難しいはずです。算数だって同じです。
植木を端から端まで3メートルおきに植えていく時、
2本植えたら、端から端までは何メートルで、
3本植えたら何メートルかという植木算の基本的な問題は、
指を折って、簡単な足し算ができるようになった子ならすぐできます。
そこで、絵を描いて考えてみることを学ぶと、たちまち応用がきくようになってきます。
子どもの頃、わたしは団地や学校の階段で、
じゃんけんしては「グーリーコ」「チヨコレイト」「パイナップル」と言いながら、
段を上り下がりする遊びをしていました。
そこで起こっていることは、旅人算について考える上で描く線分図の上で
起こっていることとよく似ています。
幼い幼児にしても、グリコばかり続くよりも、パイナップルばかり続いた方が
相手より先に進めることを体感で理解しているはずです。
そして、こうした生活に溶け込んでいる算数の概念に好奇心をくすぐられる感性を
持っているからこそ、これが子どもを惹きつける遊びになるんですよね。
虹色教室の幼児さんたちは、物を規則的に並べていくことが大好きだし、
ブロックでピラミッドのような形を作ることを喜びます。
そうした時に、算数の規則性の概念への気づきにつながるような
問いかけをしていると、算数がとても好きになっていきます。
計算のタイムを縮めるために計算プリントをこなすのでなく、
そこに勉強の動機があるのではなくて、植木を植えるために計算する……というのは、
意味を実感しやすい体験です。
そこで、ミスをして、自分の盲点となっていることに気づくことは、
その子が抱かされてきたイリュージョンを揺るがせて、素直に世界を眺めることが
できるようになるきっかけを作ってくれます。
なぜ算数を学ぶの?
という問いは、小さな本作りをしてみるだけでもすぐに理由を理解することができます。
たてとよこの長さを無視すれば、絵が貼れないとか、本の形にならないとか何らかの
不都合が生まれてくるのです。

基礎的な知識をためたり、計算を訓練したりすることは大事です。
でも、実際の暮らしのなかで、どう算数が使われているのか知り、
自分も算数を使って何かしてみて、それから訓練に戻る、
訓練からまた、どうして算数という行きつ戻りつする学びの時間を
作ってあげたいと感じています。
「ひとつのことにじっくり関われる素地」

小学3年生の女の子たちと
空気の圧力で水を飛ばす道具を作って遊びました。
うまくいかないとき、「こうかな?」「こうじゃない?」とあれこれやってみて、
やっているうちに「そうだ、こういうことやってみよ!」と閃いて、ためしています。
一人の子のアイデアで、ストローの先に空気の吹き込み口にプラスチックのコップを取りつけてみたら、
うまくいきました。
「遊び」に近い自発的な活動のなかで
何かに夢中になって関わると、学習する時の考える力の持久力が
変わってきます。

理科実験や工作の後で解いた「つるかめ算」などを面積図で解く問題。
集中して頭を使うような遊びをした後は、
見たことがない問題を解くときに、柔軟に多角的に考えて、
自力でやりきろうとする態度がアップします。
「もっと問題を出して!」とやる気が高まっていたので、
つるかめの足が200近いケースなど大きな数で問題を出しました。
すると、「結局大きい数になったって、筆算する時に(ケタが)増えるだけでしょ?」
と自分なりに基本を応用させて解いていました。

そういう姿を見ると、「あれもこれも」と将来役立ちそうな知識を詰め込んだり、
技能を訓練するよりも、
「ひとつのことにじっくり関わることを楽しめる」素地を養うことが
大事だな、と思いました。
それは「うまくいかないとき、わからないとき」に簡単に他人に頼ったり、放りだしたりしないで、
自分で試行錯誤をしていくことにつながります。
子どもの遊びの世界を豊かにすることは、
そのまま子どもたちの学力の向上につながっていくことを
今回も強く実感しました。