1740年に、グレイゼルも志賀浩二も、
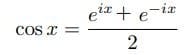
の関係を指摘している。グレイゼルは「論文」で、志賀は「手紙」において。どちらも確かめたことはないが、しかし、指数の底eはそのまま書いてあるのではなく、あとから整理されたものではないかと思う。
それは『無限解析入門』(『オイラーの無限解析』)の注に、1741年と1742年のゴールドバッハへの手紙が取り上げられていて、底が2とaの、次の式があるからである。
 (1741年)
(1741年)
 (1742年)
(1742年)
これを見ると、ベルヌーイへの手紙も、底が2のものではなかったかと思われる。
1740年から1742年にかけて、オイラーの関心は虚の指数が実の余弦になるという関係にあったと思う。それは虚の対数が実の円弧になるというベルヌーイの公式への関心と同じように、虚と実の関係である。正弦との虚の指数との関係を加えればオイラーの公式になるが、正弦との関係は1742年までは問題になっていない。
上の式を見ると分かるように、対数の形(log2、log a)がある。対数の形が制限になっているようにみえる。対数の形が消えるのはlog e = 1の場合である。いいかえれば、指数の底がeに変わることだが、この一歩がなかなか踏み出せなかったのではないかと思う。底をeにすれば、余弦と虚の指数の関係を維持するだけでなく、正弦と虚の指数との関係も可能になった。そして、指数と三角関数の関係としてのオイラーの公式ができる。これが1743年である。

指数の底の転換はどのように思いつかれたのか、興味あるところであるが、よくわからない。しかし、自由調和振動の微分方程式の成立条件ではなかったかと考えている。それは級数表示において余弦だけでなく正弦でも成立する正しい条件 log a = 1(指数の底 e)を導くからである。
(「オイラーの公式――起承転結」付録1「オイラーの公式、「起」から「承」へ」参照)
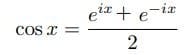
の関係を指摘している。グレイゼルは「論文」で、志賀は「手紙」において。どちらも確かめたことはないが、しかし、指数の底eはそのまま書いてあるのではなく、あとから整理されたものではないかと思う。
それは『無限解析入門』(『オイラーの無限解析』)の注に、1741年と1742年のゴールドバッハへの手紙が取り上げられていて、底が2とaの、次の式があるからである。
 (1741年)
(1741年) (1742年)
(1742年)これを見ると、ベルヌーイへの手紙も、底が2のものではなかったかと思われる。
1740年から1742年にかけて、オイラーの関心は虚の指数が実の余弦になるという関係にあったと思う。それは虚の対数が実の円弧になるというベルヌーイの公式への関心と同じように、虚と実の関係である。正弦との虚の指数との関係を加えればオイラーの公式になるが、正弦との関係は1742年までは問題になっていない。
上の式を見ると分かるように、対数の形(log2、log a)がある。対数の形が制限になっているようにみえる。対数の形が消えるのはlog e = 1の場合である。いいかえれば、指数の底がeに変わることだが、この一歩がなかなか踏み出せなかったのではないかと思う。底をeにすれば、余弦と虚の指数の関係を維持するだけでなく、正弦と虚の指数との関係も可能になった。そして、指数と三角関数の関係としてのオイラーの公式ができる。これが1743年である。

指数の底の転換はどのように思いつかれたのか、興味あるところであるが、よくわからない。しかし、自由調和振動の微分方程式の成立条件ではなかったかと考えている。それは級数表示において余弦だけでなく正弦でも成立する正しい条件 log a = 1(指数の底 e)を導くからである。
(「オイラーの公式――起承転結」付録1「オイラーの公式、「起」から「承」へ」参照)




















※コメント投稿者のブログIDはブログ作成者のみに通知されます