マックスウェルの卵形線作図法

デカルトの卵形線は、与えられた2焦点からの距離の重み付けられた和が一定となるような点の軌跡である。
2つの焦点をO₁、O₂、点をPとする。またa、bをa,b＞0 とすると、デカルトの卵形線は
　　a[O₁P]＋b[O₂P]＝一定
の関係がある。ただし、ここで[　]は距離を表す。a＝bのとき楕円になる。
「卵形線を描く」参照

マクスウェルは14歳のとき、卵形線の作図法を思いついている。それは楕円の作図法を拡張するものだった。
『ファラデーとマクスウェル』（後藤憲一著、清水書院、1993年、2016年（新装版））を読んでいて、立ち止まってしまった。
（引用はじめ）一部変更
楕円を描くのに次のような方法がある。2つの位置に針を立て、糸の端をこれらに結びつけ、鉛筆の先で糸がいつでも張っているようにしながら鉛筆を動かしていくと、針の位置を焦点とする楕円ができる。これは、楕円上の点から2つの焦点までの和が常に一定であるからである。
マックスウェルは、これを次のように拡張した。たとえば第1の焦点fからの距離と、第2の焦点Fからの距離の2倍との和が一定となる曲線を描くには、図のように、第2の焦点Fの針のところで糸をまわして、鉛筆までの間の糸が二重になるようにして描けばよい。

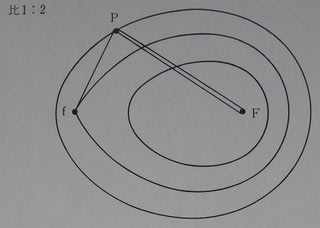
一般に、第1の点fからの距離のn倍と第2の点Fからの距離のm倍との和が一定となるような曲線は、第1の針fから鉛筆までの間の糸がn重になり、第2の針Fから鉛筆までの間の糸がm重になるようにして描けば求められる。

このようにしていろいろな形の卵形の曲線が得られる。
（引用おわり）
この作図法はエジンバラ王立協会で発表される。「卵形線の作図法については、デカルトも与えているが、本論文の方がはるかに簡単である。」（報告者ファーブス教授評）

実際に作図するのは大変だろうが、原理はわかる。