ずらし尺の√10切断とπ切断の差異

　計算尺を使ったことのある人なら，「ずらし尺」に√10切断とπ切断の２種類あることを
ご存知であろう。このずらし尺は，目外れを起こしたときに計算を継続させるための工夫
であるが，なぜ２種類あるのか？長年疑問であった。「π切断では技術計算に向いている」
と説明されているが，取扱説明書にも詳しい説明はないし，インターネットで調べても見
つからなかった。
　このたび改めてこのずらし尺を使って計算したところ，π切断では予想に反して正しい
計算結果が得られないことがあった。計算尺ではある程度の誤差は承知の上で計算するの
であるが，この誤差はちょっと大きすぎる。（このとき，学生時代の試験の答案で，先生
から「ちょっと誤差が大きすぎる」と指摘されたことを思い出した。もしかしたら，ずら
し尺を使ったためではなかったか？）

　そこで，今回自分なりにこのずらし尺について考察してみた。
　まず，ずらし尺だが，これは計算尺の上側に配置されている。

上の写真で，DF, CF, CIF尺がそれである。ずらし尺でない本来の尺は下側のCI, C, D尺であ
る。通常の乗除算ではCI, C, D尺を使う。なお，CF, CIF, CI, C尺は滑尺に配置されている。
（その他は固定尺である。）
済みません。写真の中の文字が崩れていました。π切断の説明はつぎのとおりです：
　π切断の計算尺
　上から　LL/1, LL/2, LL/3, DF
　　　　　CF, CIF, CI, C （滑尺）
　　　　　D, LL3, LL2, LL1

　ずらし尺は√10またはπで左右を入れ替えた対数目盛である。視覚的にはそうであるが，
数式では√10またはπを加算した対数目盛と捉えられる。すなわち，
　√10切断でのDFおよびCF尺は＋√10であり，π切断では＋πである。また，CIF尺はCI尺
を左右反転させたようであるが，正確にはCI尺の逆数で目盛ったものである
　√10切断では√10の逆数は
　1/√10 = 10/√10 = √10　（計算尺では「位」は任意。よって，１はまた10でもある。）
であるから，左右反転させた場合と完全に一致する。
　一方，π切断では
　1/π = 0.318
となって，両端はπとはならない。この点が√10切断の場合とは異なる。

　以下，長々と記述することは避け，問題の核心部分のみを示す。予想した結果が得られ
なかったのはCIF尺を用いた乗算であった。（これ以外は問題ないとは限らない。）例題
で説明しよう。
例．２×６の計算
　√10切断の場合とπ切断の場合の結果を下の写真に示す。

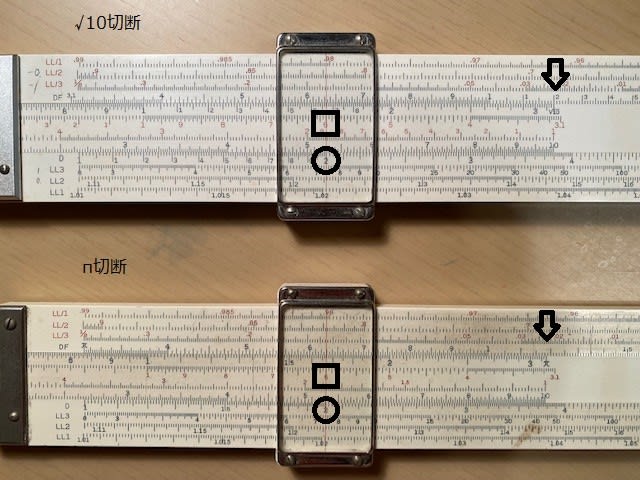
√10切断の場合は正しい結果12が得られている。しかし，π切断の方は11.84となっており，
誤差が大きい。
　このことを数式で検証してみる。
　まず，√10切断では，
　log 2 ＋ { log 6 － log (10/√10) } ＋ log √10 ＝ log 2 ＋ log 6 ＝ log (2×6) ＝ log 12 → DF
となって，真数12が答えとして求まる。
　一方，π切断では，
　log 2 ＋ { log 6 － log (10/π) } ＋ log π ＝ log ( 2×6 ) ＋ log ( π**2/10 )
　＝ log ( 12 × π**2/10 ) → DF
以上からπ切断では π**2/10 だけの誤差が発生していることがわかった。計算すると，
　12 × π**2/10 ＝ 11.84
となり，計算尺による結果と一致する。（π**2はπの二乗を意味する。）

　代数式ではつぎのようになる。
　まず，√10切断では，
　log D + { log CIF －log √10 } + log √10 = log ( D・CIF ) → DF（答え）
π切断では，
　log D + { log CIF － log ( 10 / π ) + log π = log D + log CIF + log ( π**2 / 10 )
　= log ( D・CIFπ**2 / 10 ) → DF（間違った答え）
と表せる。
　以上のとおり，√10切断では正しい答えが得られるが，π切断では答えが間違って得られ
ることがある。π切断のずらし尺を使うときはくれぐれもご注意を！
以上

前回記事への補足
百合のような花はキツネノカミソリでしょう。

実は目撃したとき，瞬時にそう思ったのですが，キツネノカミソリにしては時期が早すぎる
と思ったのです。また，色が少し違っているような気もしました。
大キツネノカミソリかも？
以上補足