オイラーは「虚対数が円弧に帰着される様式」を導いた。
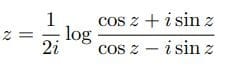
ここで、真数部分をcos zで割ると、弧zを正接を用いて、表示できる。
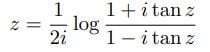 (1)
(1)
ところで、「自然対数の値を効率よく求める」で見たように、
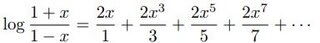
だった。ここで、x=itan z とおくと、

したがって、(1)式は

となる。ここでtan z=tとおくと、z=arc tan tとなる。

これでグレゴリーの級数が導出できた。t=1のとき、弧zはπ/4の弧に等しい。

これがライプニッツの級数である。
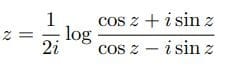
ここで、真数部分をcos zで割ると、弧zを正接を用いて、表示できる。
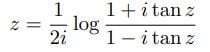 (1)
(1)ところで、「自然対数の値を効率よく求める」で見たように、
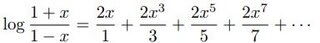
だった。ここで、x=itan z とおくと、

したがって、(1)式は

となる。ここでtan z=tとおくと、z=arc tan tとなる。

これでグレゴリーの級数が導出できた。t=1のとき、弧zはπ/4の弧に等しい。

これがライプニッツの級数である。









