アクティブマスダンパ（AMD）

「戸建住宅用のAMD制振実験レポート」

「基本型AMDの制御ループ」と「Phase2_AMDの制御ループ」は、一見すると大変よく似ていますが、アクチュエータ出力に次数の違いがあります。メインループも厳密には異なりますが、目標値が0ですから全く同一のものとして扱えます。

ローカルループにおいて「閉ループ入出力点」でクローズドループを取ると、両者とも0dBを超える所で平坦な周波数特性となり、同一のものになります。しかし、「アクチュエータ出力」は、Phase2の場合フィードバックが「比例」ですから、クローズドループと同一の周波数特性になりますが、基本型AMDの場合はフィードバックが「積分」を通るので、その前段の「アクチュエータ特性」はクローズドループに対する微分形となります。つまりローカルフィードバックによって、Phase2はリニアな特性のアクチュエータを有し、AMD基本形は微分特性のアクチュエータを有することになります。

実地テストにおいて、試しに基本型AMDのメインループのオープンループを取ってみると（狭いバンドパスで制御系を安定させた上で）、理屈どおりの位相特性が得られました。

よって、制御対象の固有値にスカイフック減衰を効かせるためのAMDは下図のような構成が基本構造になります。

関連記事：「アクティブダンパ（アクティブサスペンション）」2009-11-22

踊れ！アミーゴ

クレヨンしんちゃん「伝説を呼ぶ 踊れ！アミーゴ」

公開：2006年
監督：ムトウ ユージ

ここまで質が落ちてしまうと、「劇場版クレヨンしんちゃんシリーズ」という1つのワード（範疇）に全作品を収めることが極めて困難になります。必ずしも時系列で分割することもできませんが、アニメ史上に燦然と輝き後世に語り続けられるだろう名作と、本作のように内容らしい内容も無く、一日を待たずして忘れ去られるような凡作以下のものを、共に「劇場版クレヨンしんちゃん」と捉えることに大きな抵抗を感じています。

もちろん製作側はそんな格付けやジャンル分けなどするはずもないので、これは自分の中でやるしかありません。とはいえ、一歩引いて、あえてすべての作品をシリーズ全体として眺めれば、絶壁のような落差が存在する極めて稀なシリーズといえ、その点をシリーズの独自性と捉えるなら（そうであって欲しくはないですが）、大変興味深くも思えます。

ふと、素朴に思ったのですが、居並ぶ名作を立て続けに放った製作者達が、そのすべての手法について、手のひらを反して見せたのが、この「アミーゴ」なのだろうかとね。意図は分かりませんが。

6自由度の座標分解

赤線で描かれている直方体は剛体であり、上面は正方形とします。直方体の角に取り付けてある矢印は、直方体の動きを検出するセンサ、例えば加速度センサ等です。水色のセンサが上下方向の動きを検出するセンサ、黄色のセンサが水平方向の動きを検出するセンサで、それぞれ3個ずつ計6個あります。各センサは、座標軸の矢印方向の動きを検出するとプラス出力するものとします。

また、XYZ座標の交点は立方体の上面のセンターにあるものとし、XYZ軸を中心とする回転座標を、それぞれθX θY　θZとします。

直方体が6自由度で動いているとき、このようにセンサを取り付け、各センサの検出信号を入力として図に示す行列演算することにより、直方体をXYZおよびθX θY　θZ、それぞれの座標の動きとして個々に取り出すことができます。

入力パラメータの数値は直方体の形状、座標の位置等、上記条件においてのみこの数値になります。

（行列の計算方法は、「hパラメータとトランジスタ等価回路①」を参照してください。）

関連記事：「自由度の話」2009-11-23

自由度の話

3次元空間の物体の動きは「6自由度」といわれます。さて「自由度」とは何でしょう？
左上の図のように、ある移動点が一本の直線方向にのみ移動する（できる）場合、この移動点の動きは1自由度である、といいます。ということは、もし移動点が平面上を動けば2自由度ですね。

では右上の図のように、棒の一端を固定した場合、もう一方の先端の自由度はいくつでしょう？固定点を中心とする球面上を自由に動くので無限大自由度？ではなくて図を見ればすぐにわかりますが、移動点が何処にあってもX軸とY軸それぞれを中心とする2つの回転座標（角度）で特定できるので、棒の先端の動きは2自由度ということになります。

左下の図は、例えば電車やバスのような直方体が3個以上のバネで支持されていることを想像してください。この直方体はX座標、Y座標、Z座標それぞれの平行方向に、またX軸、Y軸、Z軸それぞれを中心とする回転方向（回転座標）に動くことができますね。よって、この直方体は6自由度です。

6自由度ということは、固有振動数はそれぞれの座標において1つ、計6つ存在しますから固有値解析や固有値設計はかなり大変な作業になるだろうことが想像できますね。

右下の図は、バネ-マス（質量）系の説明においてよく用いられる図ですが、この場合の質量Mは鉛直方向（Z方向）のみに動くことを前提としています。つまりこの図は1自由度モデルということですね。

関連記事：
「6自由度の座標分解」2009-11-25
「バネ-マス（質量）系の固有振動数」2009-11-18

アクティブダンパ（アクティブサスペンション）

「運動方程式への応用④ラプラス」
（「スカイフックダンパ」2009-11-20を参照してください）

ちょっと待て！
スカイフックダンパが素晴らしくいいのは分かったが、空中の絶対静止点なんてどこにあるんや！？　はい。そうですね。あなたの疑問はもっともです。空中の絶対静止点なんてありません。

しかし

スカイフックダンパは実現可能です。ここで初めて制御という言葉が出てくるのですが、スカイフックダンパの本質は「x'(t)に比例して力を発生するもの」ですから、制御システムとして同様の機能を構成することができるのです。

図にシステムの概念を示します。

「S」は加速度センサであり、Mに取り付けられているのでMの加速度x''(t)を検出します。センサが検出した加速度は「積分器」を経て速度x'(t)になります。「A」は電気信号が入力されることにより「力を発生するもの」で、一般にアクチュエータと呼ばれます。（アクチュエータとしてはリニアモータ等がよく用いられます。）「制御器」は入力された信号をアクチュエータ駆動電流として出力するものです。

さて、「積分器」の出力信号x'(t)は「制御器」に入力され、x'(t)に比例した駆動電流をアクチュエータに出力します。そうすると、アクチュエータはまさに「x'(t)に比例して力を発生するもの」になりますね。これがスカイフックダンパを構成するシステム：アクティブダンパの1例です。

【制御系の話】
添付のシステムブロック図は、そのまま制御ブロックも示しています。丸印に向かう2本の矢印に正負の符号が付けてあるのは、センサの検出値と目標値をここで引き算するという意味です。目標値の値はx''(t)=0ですから、ここでの差分が0になるようにアクチュエータが力を発生するわけです。この次がおもしろいのですが、アクチュエータの力によってMに発生した加速度もセンサに検出されることになりますね。それがまた丸印の所で引き算され、その差分をアクチュエータが打ち消しにいくという循環が永遠に続きます。このような制御をフィードバック制御といいます。

関連記事：「スカイフックダンパ」2009-11-20

スカイフックダンパ

「運動方程式への応用③ラプラス」

スカイフックダンパ
（アクティブダンパ）

前記事「運動方程式への応用②」では、バネ-質量系の周波数特性（振動絶縁性能）は、減衰比ζ＝C/2√(MK)の作用によって大きく変化することが確認できました。ζが小さければ高周波での振動絶縁性能は優れているけれども、固有振動数（ω0）では振動絶縁どころか、入力振動（床振動）を10倍近く増幅してしまいます。反対にζが大きければ固有振動数での増幅は小さくなりますが、高周波での振動絶縁性能は低下します。つまり、「あちらを立てればこちらが立たず」という関係で、実際にζの値を決めるときには妥協点を選ぶしかありません。

（ただし、入力振動［床振動］にも周波数成分がありますから、もし5Hz～100Hz以外の周波数成分は無視量ということであれば、バネ-質量系の固有振動数を2Hzくらいにして、ζを可能な限り小さくすれば良いわけです。）

さて、本当に欲しいのは、「あちらも立つしこちらも立つ」という都合のいい仕組みですね。つまり、固有振動数の増幅など無く、すべての周波数帯域で振動絶縁できる構造はないか？

実は、既に図で示していますが、その方法があるのです。そもそも、ζを大きくすると高い周波数での振動絶縁性能が落ちるのは、ダンパが質量と地面との間に取付けられているために

運動方程式　M x''(t)＝－C {x'(t)－x'0(t)}－K{ x(t)－x0(t)} ----- ④
に見るように

Cがx'(t)－x'0(t) の差分にかかっているため、床振動x'0(t) に対しても力を発生するからです。ならば話は簡単で、図のようにダンパの床の支持点を切り離して、空中の絶対静止点を支持点にすればよいのです。これをスカイフックダンパといい、ここではCaで表します。

では、スカイフックダンパを用いた「バネ-質量系」の運動方程式を見てみましょう。

M x''(t)＝－Ca x'(t)－K{ x(t)－x0(t)}　----- ⑧　これが運動方程式です
M x''(t)＋Ca x'(t)＋K x(t) ＝ K x0(t)

C x'0(t) が消えただけですから、ラプラス変換して伝達関数の形にすると
X / X0＝K/M / ( s^2＋sC/M＋K/M) ----- ⑨

前例にならい、式⑨を次のように変形します。
X / X0＝{√(K/M)}^2 / [ s^2＋sC/{2√(MK)}{ 2√(K/M) }＋{√(K/M)}^2]
X / X0＝ω0^2 / (s^2＋2ζω0 s＋ω0^2 )　　----- ⑩

Cc＝2√(MK)　　臨海減衰係数
ζ＝Ca/Cc 　　　減衰比
ω0＝√(K/M)　　固有振動数（rad/sec）
ω0 / 2π 　　　固有振動数（Hz）

sにjωを代入して「フーリエ変換」にします。
X / X0＝ω0^2 / (jω)^2＋j2ζω0 ω＋ω0^2 )

分母の複素数の絶対値は
[(ω0^2－ω^2)＋j2ζω0 ω]＝√{(ω0^2－ω^2)^2＋(2ζω0 ω)^2}

よって、式⑩の絶対値は
［X / X0 ］＝ω0^2 / √{(ω0^2－ω^2)^2＋(2ζω0 ω)^2}　となります。

図のグラフは「スカイフックダンパ」の伝達関数（周波数特性）です。

ζを大きくすることにより共振周波数の山はつぶれ、高い周波数の振動絶縁性能も劣化しません。また理屈上、ζはいくらでも大きくすることができます。このように、スカイフックダンパは夢のような減衰器なのです。ただ値段を聞くと目ん玉が飛び出しますね。自動車では、一部の高級車に取り付けられていたことがあるようです。

関連記事：
「アクティブダンパ（アクティブサスペンション）」2009-11-22
「運動方程式への応用②」2009-11-19

運動方程式への応用②ラプラス

周波数特性（伝達関数）

「運動方程式への応用①」(2009/11/18)　にてお話しましたように、この「バネ-質量系」は、例えば列車においては、車体と台車をシンプル化したモデルに相当します。

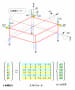
さて、電車が走りだしました。すると質量Mである車体がガタゴトと揺れ始めます。これはレールが真平らではなく、継ぎ目やゆがみなどの凹凸があるからです。このときのレールを図の地面と等価的にみれば、地面が変位x0(t)で振動していると見なすことができます。地面が振動すれば、バネとダンパを伝って力が車体に伝わり、車体は変位x(t)で揺れます。このときの運動方程式は次のようになります。（図を参照してください）

M x''(t)＝－C {x'(t)－x'0(t)}－K{ x(t)－x0(t)} ----- ④　
（ただし　x(0)＝0　x0(0)＝0）

M x''(t)＝－Cx'(t)＋Cx'0(t)－Kx(t)＋Kx0(t)
M x''(t)＋Cx'(t)＋Kx(t)＝Cx'0(t)＋Kx0(t)

この式をラプラス変換します。
Ms^2X＋CsX＋KX＝CsX0＋KX0
X / X0＝(Cs＋K) / ( Ms^2＋Cs＋K) ----- ⑤

ここで左辺は L[出力] / L[入力] ですね（出力のラプラス変換/入力のラプラス変換）。これを「伝達関数」といい周波数特性を表します。そして、周波数特性の中身は右辺ということですね。

式⑤を変形していきます。
右辺の分母分子をMでわって
X / X0＝(sC/M＋K/M) / ( s^2＋sC/M＋K/M)

ここから少し意味不明の変形をしますが、追って説明しますので、しばらく我慢してください。

X / X0＝[sC/{2√(MK)}{2√(MK)/M}＋{√(K/M)}^2]
/ [ s^2＋sC/{2√(MK)}{2√(MK)/M}＋{√(K/M)}^2]

分母分子の2√(MK)/Mは
2√(MK)/M＝(2√M√K) / (√M√M)
2√(MK)/M＝2√K / √M
2√(MK)/M＝2√(K/M)

よって
X / X0＝[sC/{2√(MK)}{2√(K/M)}＋{√(K/M)}^2]
/ [ s^2＋sC/{2√(MK)}{ 2√(K/M) }＋{√(K/M)}^2]

ここで
C/ 2√(MK)＝ζ　√(K/M)}＝ω0　として式に代入すると

X / X0＝(2ζω0 s＋ω0^2 ) / (s^2＋2ζω0 s＋ω0^2 )　　----- ⑥
このようになります。

ζ（ゼータ）＝C/ 2√(MK)は「減衰比」といい、ζ >1のときを過減衰、ζ=1のときを臨界減衰といいます。また2√(MK)は「臨界減衰係数」といい、記号Ccで表します。

つまり　ζ＝C/Cc

ω0 ＝√(K/M)　は固有振動数［共振角速度（rad/sec）］で、LC回路のω0＝1/√(LC)に相当します。固有振動数を周波数で表せば　f0(Hz)＝1/2π √(K/M)　ですね。


【フーリエ変換】

式⑥「伝達関数」のsにjωを代入すると「フーリエ変換」となり、周波数特性を得ることができます。エクセルを使って周波数特性を確認してみましょう。（ jは虚数単位 ）

まずsにjωを代入して
X / X0＝( j2ζω0 ω＋ω0^2 ) / (－ω^2＋j2ζω0 ω＋ω0^2 )　----- ⑦

分子と、分母が複素数になっているので、これの絶対値を求めます。
まずは分子から。

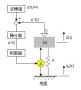
ω0^2＋j2ζω0 ω の実数部＝a、虚数部＝bとおくと　a+jb
複素数a+jbを直交座標に表せば、絶対値は0点からaとbの交点に引いた線分Cですね。
（図を参照してください）

よって、C＝√（a^2＋b^2）となります。（三平方の定理）

分子についてaとbを元に戻すと
[ω0^2＋j2ζω0 ω]＝√{(ω0^4＋(2ζω0 ω)^2}

次に分母　(ω0^2－ω^2)＋j2ζω0 ω　は
[(ω0^2－ω^2)＋j2ζω0 ω]＝√{(ω0^2－ω^2)^2＋(2ζω0 ω)^2}　

これで式⑦を書き直せば
［X / X0 ］＝ √{ω0^4＋(2ζω0 ω)^2} / √{(ω0^2－ω^2)^2＋(2ζω0 ω)^2}

となります。

f0＝ω0/2π＝2（Hz）
ω0＝4π（rad/sec）　として
この式をエクセルでグラフ化すると周波数特性は図のようになります。

このグラフは、台車から車体に伝わる振動の振幅倍率を周波数軸で見ています。またダンパによる減衰比（ζ）を変えて、4つの特性を比較しています。

まず低周波から見ていきましょう。約1Hzまでは減衰比が変わっても、振幅倍率はほぼ1ですから台車の振動がそのまま車体に伝わっています。大きく変わるのは「バネ-質量系」の固有振動数（共振周波数）である2Hzと、それ以上の周波数です。

まず固有振動数（2Hz）では減衰比＝0.1の場合、台車の振動が7倍程度増幅して車体に伝わっています。電車が動き始めて低速のときには、車体は2Hz辺りで非常によく揺れるということですね。これに対して減衰比＝0.8の場合は固有振動数での増幅は極わずかです。

しかし更に周波数が高くなればどうでしょう。例えば10Hzでみると、減衰比＝0.1の場合は台車の振動を1/10以下に低減しています。減衰比＝0.8の場合は1/3程度でしょうか。

ですから、電車の「バネ-質量系」の固有振動数や減衰費（ζ）を決める折には、電車の走行速度やレールの状態などの条件を十分考慮する必要があるということですね。

関連記事：
「運動方程式への応用①」2009-11-18
「スカイフックダンパ」2009-11-20

運動方程式への応用①ラプラス

LCRの微分方程式は、まったくそのままバネ-質量系の運動方程式に置き換えることができます。
図は、質量Mを（バネ定数Kの）バネで支持し、バネと並列に減衰器（ダンパ）Cを取り付けたモデル図です。電車であれば台車と車体との関係、自動車であればボディーとサスペンションの関係に相当します。このようなモデルを「バネ-質量系」といいます。外部からの入力が無ければ、車体重量とバネの反発力がバランスしてモデルは静止しています。

では、この「バネ-質量系」に図のようにインパルスを入力すると車体（M）はどのような動きをするでしょうか。外部から力が加わるのですから、車体に変位（位置移動）が発生しますね。この変位をｘ(t)で表します。

初めに、このモデルが静止しているときの運動方程式を示します。
（あるいは調和振動しているとき）

M d^2x(t)/dt^2＝－C dx(t)/dt－K x(t)

これを簡潔に次式のように記述してもOKです。
M x''(t)＝－C x'(t)－K x (t) 　　 ----- ①

まずM x''(t)ですが、「質量M×加速度x''(t)＝力」です。

例えば水10lが10kgであるのは、水の質量に重力加速度（9.8m/sec^2）がかかっているからです。よって10lの水を持ち上げるためには10kg以上の腕力が必要ということです。

次にC x'(t)ですが、「減衰係数C×速度 x'(t)＝力」です。これは容器に溜めたシリコンオイルを棒でかき混ぜることを想像してみてください。ゆっくり棒を動かせばさほど力は要りませんが、速く動かそうとするとより強い力が必要ですね。このように減衰成分は速度に比例して力を発生します。

最後にK x(t)はバネの反発力です。「バネ定数K×変位x(t)＝力」となります。また、減衰力とバネ力は、発生する力の方向が質量Mと逆なのでマイナスが付きます。

【コラム】
距離(変位)m / 時間s＝速度m/s　　速度m/s / 時間s＝加速度m/s^2　ですね。

それぞれの瞬時値を表す場合は
x(t)＝距離(変位)とすると、dx(t)/dt＝速度、d^2x(t)/dt^2＝加速度となります。

つまり、変位を微分すると速度、速度を微分すると加速度ということです。逆に、加速度を積分すると速度、速度を積分すると変位に戻ります。


さて、式①の減衰力と、バネ力を左辺に移項して
M x''(t)＋C x'(t)＋K x(t)＝0 ----- ②

これが「バネ-質量系」の、静止状態の微分方程式です。

そして、質量Mにインパルス［F(t)＝δ(t)］を入力した場合は
M x''(t)＋C x'(t)＋K x(t)＝δ(t)　　----- ③となります。
（ただし　x(0)＝0 ）

では、ラプラス変換して式③を解いていきましょう。

M s^2X＋C sX＋KX＝1
X＝1/ (M s^2＋C s＋K)

右辺の分母分子をMで割ると
X＝1/M / ( s^2＋sC/M＋K/M)

ここでLCR回路の式と比べてみましょう。

I＝E/L / (s^2 + sR/L + 1/LC）　-----「LCR回路の単位応答」
ね、形がそっくりでしょ？

さて、どんどんいきます。
X＝1/M / {( s＋C/2M)^2＋K/M－C^2/4M^2}

ここでパラメータに数値を入れます。
M＝4k (kg)　C＝10k (kg・m/s)　K＝600k (N/m)としましょう。質量M＝車体重量/重力加速度
（1/M＝0.25m　C/2M＝1.25　K/M＝150　 C^2/4M^2＝1.56）

X＝0.25m /{(s＋1.25)^2＋150－1.56}
X＝0.25m /{(s＋1.25)^2＋12.22}
X＝(0.25m / 12.2) 12.2 /{(s＋1.25)^2＋12.2^2}

では、f(t) = ebtsin at　　⇔　　F(s)＝a/{(s-b)^2＋a^2}　の変換式に当てはめて逆ラプラス変換します。

x(t)＝20.5μ e^－1.25 t sin 12.2 t
（ωn＝12.2　fn＝1.94Hz）

となりました。得られたx(t)を図に示します。
約2Hzの減衰波形ですね。

関連記事：
「LCR回路の過渡特性」2009-05-11
「運動方程式への応用②」2009-11-19

バネ-マス（質量）系の固有振動数

まず「質量」と「重量」の区別がつけにくいですよね。
簡単には、「質量」＝「重量」と考えてください。

つまり、私が体重計に乗ったら、体重計が示す値はだいたい70kgくらいかな？まあ70kgとしましょう。とすると私の質量[kg]は70kgです。体重とか重量とかよく言いますが、あれは質量のことを言ってるわけですね。体重計などは質量を示すように作られているということです。

でも私が地面に立っているとき、足にかかっている力（荷重）は70kgではありません。70kgはあくまでも質量です。足にかかっている力は「質量×加速度」、つまり70[kg]×9.8[m/sec^2]＝686[N]（ニュートン）ということですね。

さて

固有振動数の角速度 ω0［rad/sec］は
ω0＝√( k/M)　　-----　①　（　M：質量[kg]　k：バネ定数[N/m]　）

一方、バネ定数 k[N/m] は
k＝P/L　　-----　②　（　P：荷重[N]　L：たわみ量[m]　）

式①の平方根内は、式②より
k/M＝(P/L)/M
　　＝｛( 9.8×M)/L ｝/M　-----P[N]＝9.8×M[kg]（9.8：重力加速度[m/sec^2]）
　　＝9.8/L

従って式①は
ω0＝√( k/M)　＝√( 9.8/L)

よって固有振動数 f0[Hz} は
f0＝√( 9.8/L)/2π　　　-----　③

このように
固有振動数f0[Hz]は質量M[kg]に関与せず、バネの”たわみ量”L[m]から得られます。

例えば、たわみ量：L＝30[mm]であれば、式③より
f0＝√( 9.8/0.03)/2π
　　＝2.877[Hz]

（Thank you Mr.Og!）

f0＝2.877[Hz]において、M＝10kg とした場合のバネ定数kは
k＝P/L（P：N　L：m）
　　＝( 9.8×10）/0.03　＝3266.67
k＝3266.67[N/m]

「質量とバネ定数から固有振動数を求める場合」
M＝10[kg]、k＝1000[N/m]　とすると

式①より
ω0＝√( k/M)　＝√(1000/10)　＝10 [rad/sec]

f0＝10/2π　＝1.59 [Hz]

式②より
k＝P/L
L＝P/k ＝( 9.8×10)/1000 ＝0.098[m] ⇒98[mm]

【参考】　ω0＝√( k/M)　の導出

バネ-質量系の運動法的式は、質量の振幅変位＝x(t)とすると
M・d^2x(t)/dt^2＋k・x(t)＝0 ----- ①

x(t)＝Asinω0t ----- ②
dx(t)/dt＝ω0Acosω0t
d^2x(t)/dt^2＝－ω02Asinω0t ----- ③

式②③を式①に代入し
M (－ω0^2Asinω0t)＋kAsinω0t＝0
(－Mω0^2＋k) Asinω0t＝0
－Mω0^2＋k＝0
ω0^2＝k/M
ω0＝√( k/M)

関連記事：
「運動方程式への応用①」2009-11-18
「運動方程式への応用②」2009-11-19

あなたな～らどうする～♪

もし明日、近隣のとある国から発射されたミサイルが日本に着弾したら。そしてもし、あなたが内閣総理大臣なら、さ～てどう対応しますか？あまり考えている時間はありません。2発目が飛んできます。

核兵器は別として、通常兵器では圧倒的に日本が上回っているとするなら、日本の保有する軍事力の総力をあげて一気に殲滅しますか？これはもちろん、相手国の国民を皆殺しにすることになります。中途半端な反撃は、泥沼化することが目に見えています。イスラエルとパレスチナのようにね。

何もせず、2発目3発目以降をあまんじて受けるという手もありますね。つまり徹底的に「やる」か、まったく「やらない」かのどちらかです。

さて、いずれの場合にしても、国際社会はいったいどのように動くのでしょうか？これもなかなか読みづらいですね。

この、とても素朴でシンプルな問いに対して、誰も明確な正解を出すことはできません。ダム建設の続行や中止を決めることさえできないのですから。そしてこの事態（ミサイル着弾）はあり得ない話ではありません。

会社の、隣の席の部長は「近いうちに十中八九、勃発する」と確信しておられ、家族会議を開いて、その時もし家族が離ればなれになったら、京都の知恩院で落ち合おうと申し合わせているそうです。

とはいえ、こうやって我ら凡人が思い巡らすことくらい、とうの昔に政府はシミュレーションしているのでしょうね。裏世界の力学まで想定すれば、それがどの様なものであるのかは知る由もありませんが。

フラックスのやくわり（ハンダ付け）

母材である銅箔パターンや電子部品のリード線の表面が酸化皮膜で覆われていたり、汚れが付着していると、ハンダのぬれ性は悪くなります。そこで登場するのが「フラックス」です。

フラックスは母材の酸化皮膜や汚れを除去し、溶けたハンダの表面張力を低下させて、ぬれ性を高める働きをします。結果としてハンダの流れや作業性が飛躍的に向上し、信頼性の高い良好なハンダ付けが可能となります。よってフラックスはハンダ付けに不可欠なものと言えます。

■イモハンダ
もしフラックスを使用せずにハンダ付けを行った場合にできあがるのは、正にイモハンダです。多くの場合、ハンダ付け部を加熱しすぎて、フラックスが蒸発して無くなった状態のハンダ上がりをイモハンダと言いますが、一般化すれば「フラックスの無いハンダ付け」をイモハンダと定義することができます。

■ヤニ入りハンダ
通常、我々が使用するハンダはリールに巻かれたφ0.8～φ2.0くらいの糸ハンダですが、ほとんどの場合、フラックスを内包したヤニ入りハンダです。添付図にヤニ入りハンダの断面図を示します。
【ヤニとは「脂」（樹脂）のこと。】


フラックスの主成分はロジン（松ヤニ）です。これは常温では非活性ですが、170℃程度で活性化し、酸化皮膜除去ができるようになります。また、逆に300℃を超えると分子構造が変わり、活性を持たなくなるので注意が必要です。フラックス（ロジン）は常温では非活性であり、残留フラックスによる経時腐食の心配はありません。むしろ、ハンダおよび母材と空気との間に薄い膜をつくって、酸化防止の役目を果たします。（活性化：所定の機能が活発になること。反応性が高まること。）　


ロジン系フラックスのタイプ別

・ Rタイプ(Rosin base)　：非活性ロジンフラックス。非腐食性。
・ RMAタイプ(Mildly Activated Rosin base)　：弱活性ロジンフラックス。非腐食性。
・ RAタイプ(Activated Rosin base)　：活性ロジンフラックス。弱腐食性。

■RMAタイプはRタイプよりもハンダ付け性に優れる。RAタイプはRMAタイプよりもハンダ付け性に優れるが、わずかに腐食性がある。RMAタイプは一般的に最も多く使用されている。

〔解説〕
ロジンに少量の活性剤（酸やハロゲン物質）を入れたものが活性化ロジンで、最も一般的に用いられます。活性剤を入れることにより洗浄能力、ぬれ性が増し、ハンダ付け性が良くなるからです。活性剤の種類により、RMA（弱活性）とRA（活性）の2種類がありますが、活性剤は諸刃の剣でもあり、特にRAタイプは常温でもわずかに腐食性があります。10年以上も経った古いハンダ付けがボロボロになっていることがあるのは、このわずかな腐食性のために、主にハンダの鉛成分が腐食されたためです。

関連記事：
ハンダ付けとは 2009-11-05
“ぬれ”と“毛細管現象”2009-11-13

“ぬれ”と“毛細管現象”（ハンダ付け）

ハンダ付けの生命は“ぬれ”と“毛細管現象”といわれます。
ハンダ付けの基本原理は溶けたハンダが母材表面に広がり、母材と母材の間隙（接触面）に流れ込むことです。つまり溶けたハンダの母材表面への“ぬれ”と、間隙流入のための“毛細管現象”が重要であり、これらは溶けたハンダの表面張力に反比例します。ぬれは、ハンダ付けにおけるもっとも基本的な現象であり、ぬれを伴わないハンダ付けはあり得ません。

ハンダが銅箔パターン、及び部品のリード線にぬれることにより、富士山型のフィレット（ハンダ上げ形状）が形成されます。ハンダは毛細管現象により、スルーホールと部品リードの間隙に流入します。そして対面にもフィレットが形成されます。（左図参照）

もしハンダのぬれが悪い場合、右図のような状態になります。これは明らかにハンダ不良であり、ハンダコテの温度が低い場合や、加熱時間が短い場合に多く発生します。

温度不足や加熱不足により右図のようなハンダ形状になっても、内部にフラックスが十分残っていれば、再度ハンダコテを当てて、ハンダを適切な温度に上昇させることにより、ぬれと毛細管現象が発生し、左図のようなハンダ付け状態にすることができます。
　
この、ぬれの良し悪しを「ぬれ性」といいます。ぬれ性は、物質の流動性のみに起因するのではなく、例えば水であっても、ワックスのよく効いた車のボディーに対してはぬれにくく、油膜の剥げたボディーに対してはよくぬれます。これは感覚的に理解しやすいですね。

関連記事：
ハンダ付けとは 2009-11-05
フラックスのやくわり 2009-11-14

パケホーダイダブルの実際

私の2009年8月の通信パケット数が207,604パケットだったことは「docomo フルブラウザの注！」2009/10/30 でも触れましたが、因みに、子供が所持するケータイの通信パケット数は727,288パケットで、その内272,797パケットがフルブラウザ通信によるものでした。ワンクリックでフルブラウザが立ち上がるので、さして意識することなく（別途料金であると思わず）何回かgoogle検索などをやっていたようです。

さて、いま改めて「パケホーダイダブル」の料金システムですが、添付の図は試みとして1ヶ月スパンで傾向を見たものです。

docomoのカタログやパンフレットでは、傾斜部分が強調されて説明されており、上限の52,500パケットを超えてから先はわずかしか示されていません。よってとても合理的に見え安心感が得られます。（この料金プランは大ヒットしたことでしょう）。しかし1ヶ月スパンでみると多くの場合このようなグラフになるはずです。つまりインターネットを日常的に活用しているほぼすべての人が1週間程度で上限に達するということです。赤のラインは新規契約を終了したパケホーダイです。おそらくdocomoは「＋α」分の増益に成功したことでしょう。それで今までの赤字分が埋まったのか、黒字が増えたのかはわかりませんが。

関連記事：docomo フルブラウザの注！ 2009-10-30

hパラメータとトランジスタ等価回路②

hパラメータ

さて、では本番の「hパラメータとトランジスタ等価回路」といきましょう。　

ハイブリッド行列（h行列）

上段の式がハイブリッド行列です。前出のZ行列と比べて、ioとvoが入れ替わっているだけですね。これを再び入換えるとhパラメータはすべてインピーダンスになります。まあ、当たり前ですね。

このハイブリッド行列を連立方程式に書き換えてみましょう。

　vi=h11・ii + h12・vo ―――①
　io=h21・ii + h22・vo ―――②

式①は入力電圧に関する、式②は出力電流に関する式です。

vi=h11・ii + h12・voより、「h11・ii」と「h12・vo」は共に電圧でなければなりません。よって、電流との掛け算で表される「h11はインピーダンス（Ω）」となります。h12は単なる定数です。

同様に、io=h21・ii + h22・voより、「h21・ii」と「h22・vo」は共に電流でなければなりません。よって、電圧との掛け算で表される「h22はアドミタンス（Ω-1 または S）」となります。h21は単なる定数です。（アドミタンスはインピーダンスの逆数）

h12・vo=0 にて、h11= vi /ii となり
h11 はインピーダンス（Ω）でありhi と表します。i(input)

h11・ii=0 にて、h12= vi / vo となり
h12 は電圧帰還率（電圧増幅率の逆数）と呼びhr と表します。r(reverse)

h22・vo =0 にて、h21=io/ii となり
h21 は電流増幅率でありhf と表します。f(forward)

h21・ii=0 にて、h22=io/vo となり
h22 はアドミタンス（Ω-1）でありho と表します。o(output)

hパラメータをまとめると

　hi　入力インピーダンス（Ω）
　hr　電圧帰還率（定数）
　hf　電流増幅率（定数）
　ho　出力アドミタンス（Ω-1）

中段の式は
定義したhパラメータを用いて、行列と連立方程式に表したものです。

さて、これをトランジスタのエミッタ接地増幅回路に適用してみます。エミッタ接地増幅回路では、hパラメータの末尾にeを添えて表します。よって、行列と連立方程式は下段の式のようになります。

　vi=hie・ii + hre・vo　―――①
　io=hfe・ii + hoe・vo　―――②

式①が入力電圧に関する式、式②が出力電流に関する式です。この式を用いて「等価回路」に置き換えたものが一番下の図です。

式①より、入力電圧 vi は「hie・ii」による電圧降下(vR)と、電圧源(vs)である「hre・vo」との加算値であることが明らかです。また式②より出力電流 io は電流源(is)である「hfe・ii」と、アドミタンスと電圧の掛算値(iR)「hoe・vo」との加算値であることが明らかです。

hoe・vo は少し分かりにくいですが、式を変形して hoe・vo= vo/(1/ hoe) のようにすれば、1/ hoe はインピーダンスですから、電圧／抵抗となって hoe・vo が電流であることがよくわかりますね。

関連記事：
「hパラメータとトランジスタ等価回路①」2009-11-06
2SC1815 のhパラメータ 2010-05-04

hパラメータとトランジスタ等価回路①

連立方程式と行列

　z1=Ax+By
　z2=Cx+Dy

これはxとyを変数とする2元連立方程式ですね。A、B、C、D、は定数（パラメータ）です。この連立方程式を行列（マトリクス）で表記すると上図のようになります。

意味は、変数xをAとCに掛け、変数yをBとDに掛け、A項とB項を加算すればz1になり、C項とD項を加算すればz2になるということです。これは決めごとであり、また慣れです。おぼえましょう！慣れましょう！この行列を使うと、次に説明する2端子対回路（4端子回路）を考える時に、とても好都合なのです。

2端子対回路

2端子対回路(にたんしついかいろ、4端子回路とも)は、入力端子対と出力端子対の2組の端子からなる電気回路またはデバイス。 例えばトランジスタ、フィルタ回路などがある。2端子対回路の分析は1920年代にドイツ人の数学者Franz Breisigによって研究が始められた。
（出典: 『ウィキペディア（Wikipedia）』）
　
2端子対回路は、入力と出力の「電圧と電流」の関係に着目し、入力と出力の間にある回路を「ブラックボックス」として、内部は特有のパラメータで示します。このパラメータが決まると、回路の細部を考える必要が無くなり、回路の分析を単純化できるのです。

2端子対回路で入力と出力の電圧と電流の関係を示すパラメータの種類として

「Zパラメータ」◎
「Yパラメータ」
「hパラメータ」◎
「gパラメータ」
「Fパラメータ」

があります。これらのパラメータは行列で表現されます。

図の2端子対回路において

　vi：入力電圧
　vo：出力電圧
　ii：入力電流
　io：出力電流

A、B、C、D、はブラックボックス内のパラメータです。

Zパラメータ

下図が「Zパラメータ」です（インピーダンス行列：Z行列）。　
この行列を連立方程式に変換してみましょう。

　vi= Z11・ii + Z12・io ―――①
　vo= Z21・ii + Z22・io ―――②

式①は入力電圧に関する式、式②は出力電圧に関する式であり、すべてのZは「電流」と掛け算されその加算値が「電圧」であることから、Zはインピーダンス（Ω）であることが分かりますね。

関連記事：「hパラメータとトランジスタ等価回路②」2009-11-07