まず「質量」と「重量」の区別がつけにくいですよね。
簡単には、「質量」=「重量」と考えてください。
つまり、私が体重計に乗ったら、体重計が示す値はだいたい70kgくらいかな?まあ70kgとしましょう。とすると私の質量[kg]は70kgです。体重とか重量とかよく言いますが、あれは質量のことを言ってるわけですね。体重計などは質量を示すように作られているということです。
でも私が地面に立っているとき、足にかかっている力(荷重)は70kgではありません。70kgはあくまでも質量です。足にかかっている力は「質量×加速度」、つまり70[kg]×9.8[m/sec^2]=686[N](ニュートン)ということですね。
さて
固有振動数の角速度 ω0[rad/sec]は
ω0=√( k/M) ----- ① ( M:質量[kg] k:バネ定数[N/m] )
一方、バネ定数 k[N/m] は
k=P/L ----- ② ( P:荷重[N] L:たわみ量[m] )
式①の平方根内は、式②より
k/M=(P/L)/M
={( 9.8×M)/L }/M -----P[N]=9.8×M[kg](9.8:重力加速度[m/sec^2])
=9.8/L
従って式①は
ω0=√( k/M) =√( 9.8/L)
よって固有振動数 f0[Hz} は
f0=√( 9.8/L)/2π ----- ③
このように
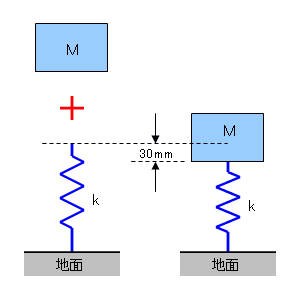
固有振動数f0[Hz]は質量M[kg]に関与せず、バネの”たわみ量”L[m]から得られます。
例えば、たわみ量:L=30[mm]であれば、式③より
f0=√( 9.8/0.03)/2π
=2.877[Hz]
(Thank you Mr.Og!)
f0=2.877[Hz]において、M=10kg とした場合のバネ定数kは
k=P/L(P:N L:m)
=( 9.8×10)/0.03 =3266.67
k=3266.67[N/m]
「質量とバネ定数から固有振動数を求める場合」
M=10[kg]、k=1000[N/m] とすると
式①より
ω0=√( k/M) =√(1000/10) =10 [rad/sec]
f0=10/2π =1.59 [Hz]
式②より
k=P/L
L=P/k =( 9.8×10)/1000 =0.098[m] ⇒98[mm]
【参考】 ω0=√( k/M) の導出
バネ-質量系の運動法的式は、質量の振幅変位=x(t)とすると
M・d^2x(t)/dt^2+k・x(t)=0 ----- ①
x(t)=Asinω0t ----- ②
dx(t)/dt=ω0Acosω0t
d^2x(t)/dt^2=-ω02Asinω0t ----- ③
式②③を式①に代入し
M (-ω0^2Asinω0t)+kAsinω0t=0
(-Mω0^2+k) Asinω0t=0
-Mω0^2+k=0
ω0^2=k/M
ω0=√( k/M)
関連記事:
「運動方程式への応用①」2009-11-18
「運動方程式への応用②」2009-11-19
簡単には、「質量」=「重量」と考えてください。
つまり、私が体重計に乗ったら、体重計が示す値はだいたい70kgくらいかな?まあ70kgとしましょう。とすると私の質量[kg]は70kgです。体重とか重量とかよく言いますが、あれは質量のことを言ってるわけですね。体重計などは質量を示すように作られているということです。
でも私が地面に立っているとき、足にかかっている力(荷重)は70kgではありません。70kgはあくまでも質量です。足にかかっている力は「質量×加速度」、つまり70[kg]×9.8[m/sec^2]=686[N](ニュートン)ということですね。
さて
固有振動数の角速度 ω0[rad/sec]は
ω0=√( k/M) ----- ① ( M:質量[kg] k:バネ定数[N/m] )
一方、バネ定数 k[N/m] は
k=P/L ----- ② ( P:荷重[N] L:たわみ量[m] )
式①の平方根内は、式②より
k/M=(P/L)/M
={( 9.8×M)/L }/M -----P[N]=9.8×M[kg](9.8:重力加速度[m/sec^2])
=9.8/L
従って式①は
ω0=√( k/M) =√( 9.8/L)
よって固有振動数 f0[Hz} は
f0=√( 9.8/L)/2π ----- ③
このように
固有振動数f0[Hz]は質量M[kg]に関与せず、バネの”たわみ量”L[m]から得られます。
例えば、たわみ量:L=30[mm]であれば、式③より
f0=√( 9.8/0.03)/2π
=2.877[Hz]
(Thank you Mr.Og!)
f0=2.877[Hz]において、M=10kg とした場合のバネ定数kは
k=P/L(P:N L:m)
=( 9.8×10)/0.03 =3266.67
k=3266.67[N/m]
「質量とバネ定数から固有振動数を求める場合」
M=10[kg]、k=1000[N/m] とすると
式①より
ω0=√( k/M) =√(1000/10) =10 [rad/sec]
f0=10/2π =1.59 [Hz]
式②より
k=P/L
L=P/k =( 9.8×10)/1000 =0.098[m] ⇒98[mm]
【参考】 ω0=√( k/M) の導出
バネ-質量系の運動法的式は、質量の振幅変位=x(t)とすると
M・d^2x(t)/dt^2+k・x(t)=0 ----- ①
x(t)=Asinω0t ----- ②
dx(t)/dt=ω0Acosω0t
d^2x(t)/dt^2=-ω02Asinω0t ----- ③
式②③を式①に代入し
M (-ω0^2Asinω0t)+kAsinω0t=0
(-Mω0^2+k) Asinω0t=0
-Mω0^2+k=0
ω0^2=k/M
ω0=√( k/M)
関連記事:
「運動方程式への応用①」2009-11-18
「運動方程式への応用②」2009-11-19
























※コメント投稿者のブログIDはブログ作成者のみに通知されます