n次元空間における単位球体の体積は、次の公式によって計算される。
n球体の体積=(n-2)球体の体積×2パイ/n
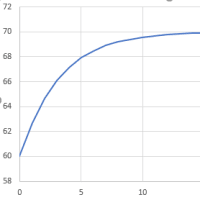
この公式に基づいて、n=4~9次元球体の体積を計算すると、3次元球体の体積を1として、4次元球体では1.18倍であり、5次元球体では1.26倍でピークとなり、nが6より大きくなるとともに体積の倍率は下がっていく。8次元球体では1.0を割って0.97倍、9次元球体では0.79倍となる。
なぜ5次元球体の体積が最大となるのかという疑問は、新たな探索の種となりえるのであるが、この問題は脇に置いておいて、ここでは9次元球体の体積というか、体積を構成する点の密度がどのような分布を示すのか、可視化してみることにする。数学的な用語を用いると、9次元球体の測度は、どのような点の分布で構成されるのか、可視的に表現したいということになるのだろう。
ユークリッド空間において、9次元空間上の点の位置は、(x1,x2,…,x9)の座標値を用いて表される。9次元単位球面は
x1^2+x2^2+…+x9^2=1
で表現できるので、この式を用いて代表点の原点からの距離を計算し、それが1以下であれば体積に寄与する点、1を越えた値であれば体積に寄与しない点として計上する。9次元球体の体積が3次元球体の0.79倍とは、前者は後者の79%の体積をもつということである。
全体的な計算技法としては、乱数によって代表点の位置を決めるモンテカルロ法を採用する。0~1の範囲の一様乱数を用いると、ほとんどの座標点が体積に寄与しないので、不適であることが分かる。代表点の多くは中心に集中する傾向が強いので、正規確率分布に基づく正規乱数を用いることになる。
正規分布の平均値を0にすることにし、標準偏差シグマを設定する。体積に寄与する代表点を80%程度にはするにはシグマの値をどの程度にしたらよいか見当をつける。シグマをおよそ0.29に設定し、座標点データを600件ぐらいとると、そのうち体積に寄与するデータは80%の前後にばらつく。正規分布から得られる乱数はゆらぐので、シグマ値の精度よりもデータ件数Nを大きくとる必要があることを知る。
N回の試行をすると、ゆらぎによる絶対誤差としてSQRT(N)程度は見積もっておかねばならない。つまり、10,000回の試行をすると、100回程度、言い換えれば1%程度の誤差はありうることになる。そうすると、2%程度の誤差を許容するならば、2,500回程度の試行をする必要があるので、データ件数を2,500件とした。およそ2,500件の試行で体積比率は79.3%+/-2%の値となった。
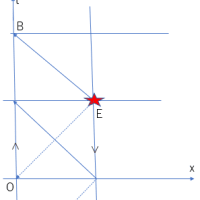
9次元空間上の体積となる代表点の集合を2次元平面に射影する。代表点がもつx1,x2,…,x9データは、いずれも乱数であるので、どの2つをとっても2次元射影点とみてよいだろう。そこで、代表点の(x1,x2)座標点の集合が体積を構成する代表点の分布とみなす。下図は、その分布図である。
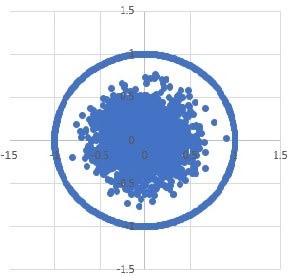
代表点の集合を囲む円は、3次元球体の2次元射影の外周を示す。
参考文献
ブライアン・ヘイズ著「数学そぞろ歩き」(共立出版)
蔵本由紀著「非線形科学」(集英社新書)
n球体の体積=(n-2)球体の体積×2パイ/n
この公式に基づいて、n=4~9次元球体の体積を計算すると、3次元球体の体積を1として、4次元球体では1.18倍であり、5次元球体では1.26倍でピークとなり、nが6より大きくなるとともに体積の倍率は下がっていく。8次元球体では1.0を割って0.97倍、9次元球体では0.79倍となる。
なぜ5次元球体の体積が最大となるのかという疑問は、新たな探索の種となりえるのであるが、この問題は脇に置いておいて、ここでは9次元球体の体積というか、体積を構成する点の密度がどのような分布を示すのか、可視化してみることにする。数学的な用語を用いると、9次元球体の測度は、どのような点の分布で構成されるのか、可視的に表現したいということになるのだろう。
ユークリッド空間において、9次元空間上の点の位置は、(x1,x2,…,x9)の座標値を用いて表される。9次元単位球面は
x1^2+x2^2+…+x9^2=1
で表現できるので、この式を用いて代表点の原点からの距離を計算し、それが1以下であれば体積に寄与する点、1を越えた値であれば体積に寄与しない点として計上する。9次元球体の体積が3次元球体の0.79倍とは、前者は後者の79%の体積をもつということである。
全体的な計算技法としては、乱数によって代表点の位置を決めるモンテカルロ法を採用する。0~1の範囲の一様乱数を用いると、ほとんどの座標点が体積に寄与しないので、不適であることが分かる。代表点の多くは中心に集中する傾向が強いので、正規確率分布に基づく正規乱数を用いることになる。
正規分布の平均値を0にすることにし、標準偏差シグマを設定する。体積に寄与する代表点を80%程度にはするにはシグマの値をどの程度にしたらよいか見当をつける。シグマをおよそ0.29に設定し、座標点データを600件ぐらいとると、そのうち体積に寄与するデータは80%の前後にばらつく。正規分布から得られる乱数はゆらぐので、シグマ値の精度よりもデータ件数Nを大きくとる必要があることを知る。
N回の試行をすると、ゆらぎによる絶対誤差としてSQRT(N)程度は見積もっておかねばならない。つまり、10,000回の試行をすると、100回程度、言い換えれば1%程度の誤差はありうることになる。そうすると、2%程度の誤差を許容するならば、2,500回程度の試行をする必要があるので、データ件数を2,500件とした。およそ2,500件の試行で体積比率は79.3%+/-2%の値となった。
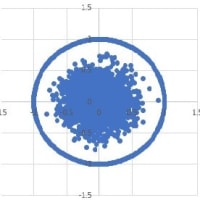
9次元空間上の体積となる代表点の集合を2次元平面に射影する。代表点がもつx1,x2,…,x9データは、いずれも乱数であるので、どの2つをとっても2次元射影点とみてよいだろう。そこで、代表点の(x1,x2)座標点の集合が体積を構成する代表点の分布とみなす。下図は、その分布図である。

代表点の集合を囲む円は、3次元球体の2次元射影の外周を示す。
参考文献
ブライアン・ヘイズ著「数学そぞろ歩き」(共立出版)
蔵本由紀著「非線形科学」(集英社新書)











※コメント投稿者のブログIDはブログ作成者のみに通知されます