2次元結晶群とは、2次元平面を隙間なくタイル張りするような結晶格子群のことを言う。結晶格子を構成する単位正多角形は、正三角形、正方形および正六角形に限られる。ただ、これら正多角形格子上の適当な点を結ぶと、平行四辺形(菱形)の格子を構成できる。2次元結晶群は17種類に分類できる。
壁紙群または文様群と呼ばれる平面状の文様繰り返しパターンは、2次元結晶格子に基づいているので、その規則的パターンは17種類しかない。よって日本の伝統的な文様は、この17種類のパターンのいずれかに属することになる。
17種のパターンは、次の4つの対称性の組合せによって分類されている。並進対称性、回転対称性(60度、90度、120度、180度であり、各々6、4、3、2回の対称性)、鏡映(鏡像対称性)および映進(並進と鏡映の組合せ)の4つである。同一パターン中の文様図形はすべて同じ大きさで並進しており、回転対称性、鏡映や映進がそのパターン内の変異となる。数学的には、これら並進、回転、鏡映は合同変換となり、図形の合同変換の全体(各パターン)は合同変換群と呼ばれる群をつくる。
高次元結晶、たとえば5次元結晶は、5次元超立方格子の構造をもつ。各格子点には原子が配列される。各格子点の位置は、5次元座標系上の座標値(k1,k2,k3,k4,k5)で表される。k1~k5は整数である。
超立方格子(k1,k2,k3,k4,k5)に一次変換の行列を施したものの座標値を(x,y,u,v,w)で表す。ここで5行5列の行列の要素は、5回対称性(72度間隔)を示すように設定される。
u,v,wで表す3次元空間は、窓空間と呼ばれる。5次元超立方体を窓空間に射影すると、菱形20面体が生じるが、この立体内に存在する点のみを2次元平面に射影することになる。
このようにして構築した2次元格子は、ペンローズ・タイリングと呼ばれ、二種類の菱形で構成される図形となる。
下図は、ペンローズ・タイリングの一部のみを示すものであり、二つの菱形20面体の2次元射影を示す。
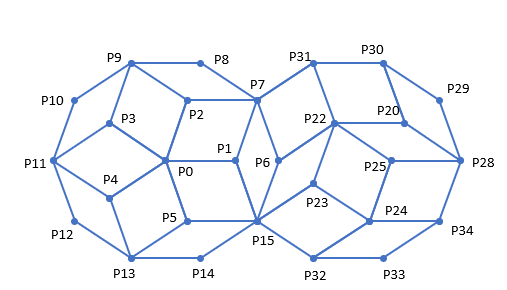
2次元平面上の格子点(u,v)は、次の式で表現される。
u=SQRT(2/5)×(k1+k2cos2a+k3cos4a+k4cos6a+k5cos8a)
v=SQRT(2/5)×(k2sin2a+k3sin4a+k4sin6a+k5sin6a)
ここでa=2パイ/5である。
図で点P0は、k1~k5=0、すなわち(u,v)=(0,0)となる原点である。P1は、(u,v)=(1,0)、すなわちk1=1,k2~k5=0となる点である。P3は、ベクトルP1を順方向に2aだけ回転させたベクトルであるから、その(u,v)は(cos2a,sin2a)、すなわちk1=0,k2=1,k3~k5=0となる。
2次元平面(u,v)を複素平面とみなすと、一般にu軸の順方向からの角度tをもつベクトルP1を角度2aだけ回転させたベクトルP3の位置は、(cos(t+2a),sin(t+2a))となる。そうすると、P3から角度2aだけ回転させたベクトルP5の位置は、(cos4a,sin4a)、すなわちk1,k2=0,k3=1,k4,k5=0、同様にしてベクトルP2の位置は、(cos6a,sin6a); k1~k3=0,k4=1,k5=0、ベクトルP4の位置は(cos8a,sin8a);k1~k4=0,k5=1となる。
uのcos関数表示およびvのsin関数表示は、各々cos2a~cos8aおよびsin2a~sin8aを基底とする代数式とみなすことができ、2つの代数式の間で加減算をすることができる。たとえば点P7の位置を求めるために、ベクトルP1,P2の複素数表示をすると、P1=1; P2=cos6a+isin6aであるからベクトルP7の位置は、(1+cos6a)+isin6aとなる。つまり点P7は、ベクトルP1とP2がつくる平行四辺形P0P1P7P2の頂点に相当する。代数式による計算結果は、(1+cos6a,sin6a)、すなわちk1=1,k4=1,k2,k3,k5=0になる。
ここではP0は原点であるが、仮にP0が原点でない場合でも、P1,P2,P0,P7を代数式表示したものの実数部分(u)をこの記号で表すと、P7=P1+P2-P0の代数式計算によってP7の位置(k1~k5)が求められる。
点P6,P8~P15についても、位置ベクトルの回転角度によるか、あるいは平行四辺形の対角頂点にあることを利用し、代数式の計算によって、これら点の位置を求めることができる。
菱形20面体の射影の外枠P6~P15の隣の外枠P1,P7,P15,P28~P34は、各々対応する点がu軸の順方向に+(k1,k2,k3,k4,k5)=+(1,-1,0,0,-1)だけ平行移動している。したがって、前者の各点の(k1,k2,k3,k4,k5)にこの平行移動分を加えれば、後者の対応する点の位置(k1,k2,k3,k4,k5)が得られる。特に、P7,P15のように隣接する外枠上で共有する点の位置が確定している場合には、このような共有点の位置から平行移動分を得ることができる。
後者の射影外枠内の点P6,P20,P22~P25については、各点を対角頂点とするような平行四辺形の2つの頂点の位置(k1~k5)から代数計算によってその位置を求めることができる。
下図は、先の菱形20面体の2次元射影図形から出発して、ペンローズ・タイリングの範囲を拡張したものである。

この超立方格子点の位置は、5つの整数の組によって表現される。この超立方格子から2次元平面を隙間なくタイル張りするような図形を得る操作は、数論幾何学の分野に属するのだろうか。
参考文献
文様と結晶構造に関するインターネット記事のほかに、
数学セミナー2021年9月号:石原慶一著「高次元立方体の断面としてみた結晶構造」(日本評論社)
壁紙群または文様群と呼ばれる平面状の文様繰り返しパターンは、2次元結晶格子に基づいているので、その規則的パターンは17種類しかない。よって日本の伝統的な文様は、この17種類のパターンのいずれかに属することになる。
17種のパターンは、次の4つの対称性の組合せによって分類されている。並進対称性、回転対称性(60度、90度、120度、180度であり、各々6、4、3、2回の対称性)、鏡映(鏡像対称性)および映進(並進と鏡映の組合せ)の4つである。同一パターン中の文様図形はすべて同じ大きさで並進しており、回転対称性、鏡映や映進がそのパターン内の変異となる。数学的には、これら並進、回転、鏡映は合同変換となり、図形の合同変換の全体(各パターン)は合同変換群と呼ばれる群をつくる。
高次元結晶、たとえば5次元結晶は、5次元超立方格子の構造をもつ。各格子点には原子が配列される。各格子点の位置は、5次元座標系上の座標値(k1,k2,k3,k4,k5)で表される。k1~k5は整数である。
超立方格子(k1,k2,k3,k4,k5)に一次変換の行列を施したものの座標値を(x,y,u,v,w)で表す。ここで5行5列の行列の要素は、5回対称性(72度間隔)を示すように設定される。
u,v,wで表す3次元空間は、窓空間と呼ばれる。5次元超立方体を窓空間に射影すると、菱形20面体が生じるが、この立体内に存在する点のみを2次元平面に射影することになる。
このようにして構築した2次元格子は、ペンローズ・タイリングと呼ばれ、二種類の菱形で構成される図形となる。
下図は、ペンローズ・タイリングの一部のみを示すものであり、二つの菱形20面体の2次元射影を示す。

2次元平面上の格子点(u,v)は、次の式で表現される。
u=SQRT(2/5)×(k1+k2cos2a+k3cos4a+k4cos6a+k5cos8a)
v=SQRT(2/5)×(k2sin2a+k3sin4a+k4sin6a+k5sin6a)
ここでa=2パイ/5である。
図で点P0は、k1~k5=0、すなわち(u,v)=(0,0)となる原点である。P1は、(u,v)=(1,0)、すなわちk1=1,k2~k5=0となる点である。P3は、ベクトルP1を順方向に2aだけ回転させたベクトルであるから、その(u,v)は(cos2a,sin2a)、すなわちk1=0,k2=1,k3~k5=0となる。
2次元平面(u,v)を複素平面とみなすと、一般にu軸の順方向からの角度tをもつベクトルP1を角度2aだけ回転させたベクトルP3の位置は、(cos(t+2a),sin(t+2a))となる。そうすると、P3から角度2aだけ回転させたベクトルP5の位置は、(cos4a,sin4a)、すなわちk1,k2=0,k3=1,k4,k5=0、同様にしてベクトルP2の位置は、(cos6a,sin6a); k1~k3=0,k4=1,k5=0、ベクトルP4の位置は(cos8a,sin8a);k1~k4=0,k5=1となる。
uのcos関数表示およびvのsin関数表示は、各々cos2a~cos8aおよびsin2a~sin8aを基底とする代数式とみなすことができ、2つの代数式の間で加減算をすることができる。たとえば点P7の位置を求めるために、ベクトルP1,P2の複素数表示をすると、P1=1; P2=cos6a+isin6aであるからベクトルP7の位置は、(1+cos6a)+isin6aとなる。つまり点P7は、ベクトルP1とP2がつくる平行四辺形P0P1P7P2の頂点に相当する。代数式による計算結果は、(1+cos6a,sin6a)、すなわちk1=1,k4=1,k2,k3,k5=0になる。
ここではP0は原点であるが、仮にP0が原点でない場合でも、P1,P2,P0,P7を代数式表示したものの実数部分(u)をこの記号で表すと、P7=P1+P2-P0の代数式計算によってP7の位置(k1~k5)が求められる。
点P6,P8~P15についても、位置ベクトルの回転角度によるか、あるいは平行四辺形の対角頂点にあることを利用し、代数式の計算によって、これら点の位置を求めることができる。
菱形20面体の射影の外枠P6~P15の隣の外枠P1,P7,P15,P28~P34は、各々対応する点がu軸の順方向に+(k1,k2,k3,k4,k5)=+(1,-1,0,0,-1)だけ平行移動している。したがって、前者の各点の(k1,k2,k3,k4,k5)にこの平行移動分を加えれば、後者の対応する点の位置(k1,k2,k3,k4,k5)が得られる。特に、P7,P15のように隣接する外枠上で共有する点の位置が確定している場合には、このような共有点の位置から平行移動分を得ることができる。
後者の射影外枠内の点P6,P20,P22~P25については、各点を対角頂点とするような平行四辺形の2つの頂点の位置(k1~k5)から代数計算によってその位置を求めることができる。
下図は、先の菱形20面体の2次元射影図形から出発して、ペンローズ・タイリングの範囲を拡張したものである。

この超立方格子点の位置は、5つの整数の組によって表現される。この超立方格子から2次元平面を隙間なくタイル張りするような図形を得る操作は、数論幾何学の分野に属するのだろうか。
参考文献
文様と結晶構造に関するインターネット記事のほかに、
数学セミナー2021年9月号:石原慶一著「高次元立方体の断面としてみた結晶構造」(日本評論社)









