自然科学ダイアログで「あらためて問う「情報とはなにか?」-自然科学の新たな情報の捉え方」と題するダイアログをすることになった機会に、私が発表した見解について、ブログに記録を残すことにした。
数学でいう位相幾何学は、図形を自由にのばしたり、ちぢめたり、曲げたり、まっすぐにしたりしても変わらない性質(位相不変性)を研究する分野であり、そのような幾何学的な変形によって変わらない数学的な量を一般に不変量と呼んでいる。
また、物理学では、物体が運動することによって変わらない物理量や、分子集団の中で個々の分子がランダムに運動しても分子集団全体として保存される物理量、すなわち保存量が存在し、これは数学でいう不変量に相当する。物理学には、様々の対称性が存在し、対称性はあまねく物理量の保存則に従うことが証明されている。すなわち、力学系に対称性があれば、何らかの不変量が存在するのである。ただしこの仮説にも例外はあるようだ。
保存量または不変量がそのまま情報として扱える例をいくつか挙げる。
例1: 江戸時代に書かれた古文書の手書き文字が現在でも読めるのは、書かれた文字および単語が不変量であり、時代を超えて共通の認識をもてる情報だからである。
例2: 生命体がもつDNA上に記録された遺伝コードは、基本的には世代を越えて伝達され、生命体を形づくるための設計図になるという観点からみれば、同じ生物種についてほぼ不変量であり、情報に他ならない。ただ、生物進化の過程を通じて遺伝コードに生じる突然変異が自然淘汰によって世代を越えて保存されると、別の生物種が誕生することがあり、それが生物多様性をさらに拡大させることになる。
例3: 物質が拡散してもその量は保存される。仮想的な面Sを通して、単位時間、単位面積あたりに移動する物質の量が保存されるという保存則を用いれば、拡散方程式および熱伝導の方程式を導くことができる。熱量は、物質の量に付随する数量である。
例4: 保存力学系は、たとえば分子集団の運動を記述する力学系であり、エントロピー生成をともなわない過程を特徴とする。n個の分子から成る集団の中で、各々の分子がランダムな方向と速度を伴って移動しても、力学系全体のエネルギーは保存される。各分子は、相空間とよばれる6n次元空間内の一定なエネルギーの曲面上をあたかも流体の流線を描くように動く。系のエネルギーが保存されるとは、このエネルギー曲面上の単位球面の体積が保存されることを意味する。つまり系の全エネルギーは、位相幾何学でいう位相不変量に相当するのである。
散逸力学系は、熱対流のような現象の状態を表す力学モデルであり、たえずエントロピーを生成しては外部に排出する非平衡開放系である。以下、散逸力学系において、どのように情報が取り扱われるのかについて例示する。
情報理論でいう情報という概念は、人間の価値観がともなっている。しかし、そのような価値観を無視して物理的媒体に格納された情報を一括して物理的に操作する場合には、情報がもつエントロピーにマイナス符号をつけて負のエントロピーで表現するだけで、物理的なエントロピーに変換できる。すなわち、1と0がランダムに並んでいるような情報のエントロピーが最も小さく、すべてのビット列が0であるような情報のエントロピーが最大となると考える。そのように考えてよい理由は、力学系を構成する個々の分子が、1と0の並びで計数できると仮定される「状態」という情報をもっているからである。
コンピュータのメモリ上の情報を消去し、すべてのビット列が0になるようにリセットすると、物理的なエントロピー増大となるので、外部からもらう熱エネルギーが消去動作に使われるとともにその一部エネルギーが外部に散逸する。
逆に、情報0にリセットしたメモリをエネルギー源として利用することができる。「情報エンジン」と呼ばれる。情報エンジンを利用すると、放出されたエネルギーによって何らかの仕事ができるとともに、メモリ上の秩序あるビット列0をランダムに1と0が並ぶビット列に変換する。すなわち物理的エントロピーは減少するが、情報としてのエントロピーは増大する。
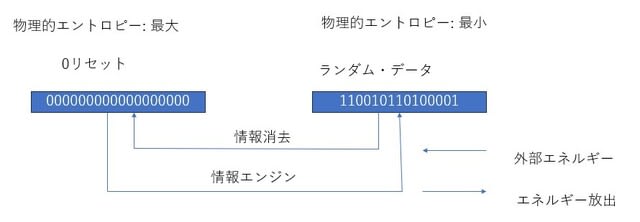
人間の価値観によれば、規則正しいパターンをもつ情報が頻度高く現れてほしく、ランダム・データはサプライズである。一方、力学系においては、ランダム・データに近いパターンをもつ情報が頻度高く現れ、規則正しいパターンをもつ情報が現れることは稀な現象であり、サプライズである。物理的なエントロピー量と、情報理論のエントロピー量とが反対符号の同一量となっているのは、まことにシンプルかつ合理的な体系である。
私がこのシンプルな見解をダイアログの場で発表したとき、情報工学を専攻したというメンバーから異議ありと思われるコメントをいただいた。私の見解に対してご批判をいただきたいです。
自由エネルギー原理に基づく脳理論では、脳は、感覚器官から入力された感覚信号から「隠れ状態」を能動的に推論するプロセスを実行する。熱力学で脳の内部エネルギーからそのエントロピーが決まり、エントロピーから状態が決まると仮定されている。
意識の分野では、さまざまな神経細胞集団で情報交換が行われ、情報が統合されることで意識が生じるとする統合情報理論が提唱されている。この理論は、情報の統合度合いを示す指標を定義し、これをもとに脳の意識の度合を測ろうとする。この指標は、「情報量」と、その情報量が「統合」されているか否かという二つのファクターによって決まる。
情報理論によれば、システムを構成する要素の状態数が少ない場合には、システムがとりうるパターンの数が少ないということであり、規則性が高いということであり、情報を少量のビット数で表現できるので情報量が小さい。逆にシステムの状態数が多い場合には、ランダム性が高いということであり、情報を表現するには多量のビット数が必要になるので、情報量が大きい。
「情報量」と「統合」の有意な組合せは、両者が大きいケースと、いずれか一方が大きく他方が小さいケースの3通りある。情報量が大きくても、要素間の情報交換のためのリンクが少ない(統合の度合が小さい)ケースでは、統合指標は低くなる。また個々の要素が他のすべての要素との間にリンクをもつような統合の度合が大きいケースでは、リンク接続が規則的になるため、リンク間でやりとりされる平均情報量が小さくなり、指標は低くなる。人間の脳のように両者ともに大きいケースでは、指標の値が高くなる。
参考文献
乾敏郎他著「脳の大統一理論」(岩波科学ライブラリ)
数学でいう位相幾何学は、図形を自由にのばしたり、ちぢめたり、曲げたり、まっすぐにしたりしても変わらない性質(位相不変性)を研究する分野であり、そのような幾何学的な変形によって変わらない数学的な量を一般に不変量と呼んでいる。
また、物理学では、物体が運動することによって変わらない物理量や、分子集団の中で個々の分子がランダムに運動しても分子集団全体として保存される物理量、すなわち保存量が存在し、これは数学でいう不変量に相当する。物理学には、様々の対称性が存在し、対称性はあまねく物理量の保存則に従うことが証明されている。すなわち、力学系に対称性があれば、何らかの不変量が存在するのである。ただしこの仮説にも例外はあるようだ。
保存量または不変量がそのまま情報として扱える例をいくつか挙げる。
例1: 江戸時代に書かれた古文書の手書き文字が現在でも読めるのは、書かれた文字および単語が不変量であり、時代を超えて共通の認識をもてる情報だからである。
例2: 生命体がもつDNA上に記録された遺伝コードは、基本的には世代を越えて伝達され、生命体を形づくるための設計図になるという観点からみれば、同じ生物種についてほぼ不変量であり、情報に他ならない。ただ、生物進化の過程を通じて遺伝コードに生じる突然変異が自然淘汰によって世代を越えて保存されると、別の生物種が誕生することがあり、それが生物多様性をさらに拡大させることになる。
例3: 物質が拡散してもその量は保存される。仮想的な面Sを通して、単位時間、単位面積あたりに移動する物質の量が保存されるという保存則を用いれば、拡散方程式および熱伝導の方程式を導くことができる。熱量は、物質の量に付随する数量である。
例4: 保存力学系は、たとえば分子集団の運動を記述する力学系であり、エントロピー生成をともなわない過程を特徴とする。n個の分子から成る集団の中で、各々の分子がランダムな方向と速度を伴って移動しても、力学系全体のエネルギーは保存される。各分子は、相空間とよばれる6n次元空間内の一定なエネルギーの曲面上をあたかも流体の流線を描くように動く。系のエネルギーが保存されるとは、このエネルギー曲面上の単位球面の体積が保存されることを意味する。つまり系の全エネルギーは、位相幾何学でいう位相不変量に相当するのである。
散逸力学系は、熱対流のような現象の状態を表す力学モデルであり、たえずエントロピーを生成しては外部に排出する非平衡開放系である。以下、散逸力学系において、どのように情報が取り扱われるのかについて例示する。
情報理論でいう情報という概念は、人間の価値観がともなっている。しかし、そのような価値観を無視して物理的媒体に格納された情報を一括して物理的に操作する場合には、情報がもつエントロピーにマイナス符号をつけて負のエントロピーで表現するだけで、物理的なエントロピーに変換できる。すなわち、1と0がランダムに並んでいるような情報のエントロピーが最も小さく、すべてのビット列が0であるような情報のエントロピーが最大となると考える。そのように考えてよい理由は、力学系を構成する個々の分子が、1と0の並びで計数できると仮定される「状態」という情報をもっているからである。
コンピュータのメモリ上の情報を消去し、すべてのビット列が0になるようにリセットすると、物理的なエントロピー増大となるので、外部からもらう熱エネルギーが消去動作に使われるとともにその一部エネルギーが外部に散逸する。
逆に、情報0にリセットしたメモリをエネルギー源として利用することができる。「情報エンジン」と呼ばれる。情報エンジンを利用すると、放出されたエネルギーによって何らかの仕事ができるとともに、メモリ上の秩序あるビット列0をランダムに1と0が並ぶビット列に変換する。すなわち物理的エントロピーは減少するが、情報としてのエントロピーは増大する。

人間の価値観によれば、規則正しいパターンをもつ情報が頻度高く現れてほしく、ランダム・データはサプライズである。一方、力学系においては、ランダム・データに近いパターンをもつ情報が頻度高く現れ、規則正しいパターンをもつ情報が現れることは稀な現象であり、サプライズである。物理的なエントロピー量と、情報理論のエントロピー量とが反対符号の同一量となっているのは、まことにシンプルかつ合理的な体系である。
私がこのシンプルな見解をダイアログの場で発表したとき、情報工学を専攻したというメンバーから異議ありと思われるコメントをいただいた。私の見解に対してご批判をいただきたいです。
自由エネルギー原理に基づく脳理論では、脳は、感覚器官から入力された感覚信号から「隠れ状態」を能動的に推論するプロセスを実行する。熱力学で脳の内部エネルギーからそのエントロピーが決まり、エントロピーから状態が決まると仮定されている。
意識の分野では、さまざまな神経細胞集団で情報交換が行われ、情報が統合されることで意識が生じるとする統合情報理論が提唱されている。この理論は、情報の統合度合いを示す指標を定義し、これをもとに脳の意識の度合を測ろうとする。この指標は、「情報量」と、その情報量が「統合」されているか否かという二つのファクターによって決まる。
情報理論によれば、システムを構成する要素の状態数が少ない場合には、システムがとりうるパターンの数が少ないということであり、規則性が高いということであり、情報を少量のビット数で表現できるので情報量が小さい。逆にシステムの状態数が多い場合には、ランダム性が高いということであり、情報を表現するには多量のビット数が必要になるので、情報量が大きい。
「情報量」と「統合」の有意な組合せは、両者が大きいケースと、いずれか一方が大きく他方が小さいケースの3通りある。情報量が大きくても、要素間の情報交換のためのリンクが少ない(統合の度合が小さい)ケースでは、統合指標は低くなる。また個々の要素が他のすべての要素との間にリンクをもつような統合の度合が大きいケースでは、リンク接続が規則的になるため、リンク間でやりとりされる平均情報量が小さくなり、指標は低くなる。人間の脳のように両者ともに大きいケースでは、指標の値が高くなる。
参考文献
乾敏郎他著「脳の大統一理論」(岩波科学ライブラリ)









