クラドニ図形のコンピュータ・シミュレーション

　テレビのサイエンス・ショウで、クラドニ図形を作成する実験を見た。振動させる正方形板を中心で支えて、板の上に細かい砂を一面にまいておいて、ふちをバイオリンの弓でこする。板に固有振動がおこると、砂は節線の所に集まって、いわゆるクラドニ図形が現れる。

　そこで、この際、コンピュータ上でクラドニ図形をシミュレートして可視化できるものか試行することにした。

　計算に当たっては、参考文献の実験値を利用させてもらうことにした。この実験は、アクリルの円板上に粒子をまいておいて、円板中心の下部に加振器を設け、円板に色々な周波数の振動を与える。振動数が円板の固有振動数になったとき、円板上に同心円状のクラドニ図形が現れる。円板は、動径（ｒ）方向にリングを節とする定常波の形態で振動していることを示している。また、隣接する二つのリングを結ぶ放射状の線も見られる。

　円板が固有振動モードになったとき、円板の振動は、動径方向の振動と偏角方向の振動とを重ね合わせたものになると考える。しかし、今回のシミュレーションでは、計算を簡単にするために、動径方向の振動のみに着目することにした。計算結果の数値にこだわるよりも固有振動モードという概念の可視化に重点をおくためでもある。

　円板の半径は約８．７ｃｍであり、得られている実験値は次の通りである。
　　　振動数（Ｈｚ）　リングの数　波長（ｃｍ）
　　　　　３９５　　　　　　２　　　　　　５．８
　　　　　６２２　　　　　　３　　　　　　４．４
　　　　１０４９　　　　　　４　　　　　　３．５

　円板の中心は振動の湧き出し口になるので、複雑な振動波形となるであろう。中心に最も近い第１リング以後の動径ｒで安定な振動波形が得られているであろう。

　第１リングと第２リング、第２リングと第３リング、第３リングと第４リングの間隔は、いずれも波長／２になっていると仮定した。また、最終リングから円板のふちまでは開放端であるので、波長／４になっていると仮定した。

　この仮定をおくと、円板の中心から第１リングまでの間隔が計算できる。結果は、固有振動数の小さいものから順に４．３，３．２，２．６ｃｍであり、振動数が上がるに従ってその間隔が小さくなる。

　円板を打つなどすると振動するが、摩擦抵抗のために減衰振動となってやがて振動は停止する。加振器などにより円板に強制振動を加えると、振動は持続する。特に、外力の角振動数ｗが円板の固有角振動数ｗ0に一致するとき、その振幅は最大値をとる。この現象は共振と呼ばれている。

　円板は複数の固有振動モードをもつという観点からみれば、円板の振動は弦の振動と似ている。しかし、動径方向（ｒ方向）のほかに偏角方向の振動が加わるので、弦の振動と同じではない。また、弦の振動と異なり、振動の湧き出し口があったり、動径方向の境界条件や円板面と垂直な方向の境界条件が異なり、複雑である。このため、固有振動数とリング数との間の関係式は得られない。

　ここでは、固有振動数はともかくとして、リング数３の固有振動モードをシミュレーションの対象とした。

　円板の上面をｘｙ平面上においたとき、ｚ方向の振動による垂直変位の境界条件は、ｚ＞０側で自由端、ｚ＜０側で円板実体から抗力を受けるので、ｚ＞０側の振幅ａuはｚ＜０側の振幅ａdより大きくなるであろう。

　ｚ方向の変位は、平均場の理論に従うとすれば、円板のｚ方向の変位の時間平均は、振幅が（ａu－ａd）／２の平均値となり、振動を表す関数は、この平均振幅と、たとえばｓｉｎｒのように時間によらない場所だけの関数をもつ仮想振動パターンで定義できるだろう。この仮想振動モデルによって計算が容易になるので都合がよい。

　ここで、この仮想振動モデルを検証するとともに、平均振幅を求める概略計算を行っておこう。

　リング間に置かれた粒子が、微小な傾斜角度ｔをもつ摩擦抵抗のない長さ１１ｍｍほどの仮想斜面を１秒くらいの時間でリング節まで滑り落ちるとすると、落体の法則から
　　　１１＝ｇｓｉｎｔ×１＾２／２～＝ｇｔ／２
が成り立つ。ｇは重力の加速度９．８ｍ／ｓｅｃ＾２である。

　そうすると、平均振幅～＝１１ｔによって、平均振幅が概略計算できる。結果は０．０２ｍｍとなるので、このモデルを許容してよいだろう。

　この場合、仮想斜面の形状がｓｉｎｒのような振動につきものの三角関数であるか否かは問題ではないので、直線状の斜面で置き換えて構わない。

　ここまでくると、シミュレーションをするまでもなく、その結果がみえてくるが、簡単なコンピュータ・シミュレーションを行って確認しておこう。

　Ｅｘｃｅｌを用いて、３．２＜ｒ＜８．７の範囲の動径ｒと０＜ｔ＜２＊ＰＩ（）の範囲の偏角ｔについてそれぞれ約１０００個の一様乱数をとって値を貼り付ける。各データ点は、円板上にばらまいた粒子を表現している。

　各粒子が上記のような仮想振動モデルに従って移動するとすれば、各粒子は１秒程度の時間を経て、ｒ＝３．２，５．４，７．６のいずれかに集結するであろう。粒子は、リング間の中点を境界として低位のリングまたは高位のリングに向けて移動するであろうから、粒子のｒ位置を５つのケースに場合分けして、各々の集結先まで移動させることにした。もし粒子が振動のリング節またはリング間の中点にあれば、移動せずその位置にとり残されることになる。

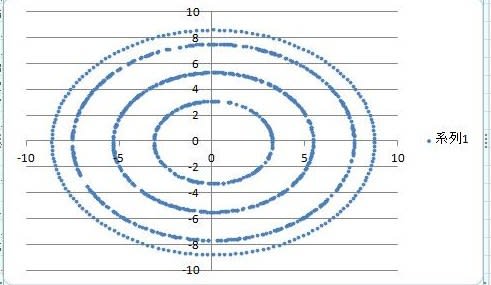
　移動後の粒子の位置を（ｒ，ｔ）座標から（ｘ，ｙ）座標に変換し、グラフ表示する。下図にそのグラフを示す。



　参考文献
　谷口駿一著「クラドニ図形による固有振動モードの解析」（インターネット）

スプライン曲線で花びらを描く

　１月２７日付のブログで紹介したスプライン曲線の続きとして、最小限のデータ点を与えてスプライン補間し、花びらのような閉曲線を描けるのか否か試してみることにした。

　花びらのデータ（ｘj，ｙj）；（ｊ＝１，２，．．．，Ｎ）は、平面データであるから、一価関数の形をしていない。そこで、データ点の位置を極座標で表現することにし、データ点の位置を示す動径ｒは偏角ｔの関数とみる。ｔは０から２パイまでの区間に存在すればよい。

　花びらは５弁とし、花びら図形の山の頂点で５点、谷の頂点で５点、合計１０点のデータ点をとり、これらデータ点の間をスプライン補間するものとする。山の頂点でｒ＝６、谷の頂点でｒ＝２としてみた。

　花びら山を中点とする区間と花びら谷を中点とする区間の大きさを均等にとるのではなく、パイ／１５を１単位として前者では４単位、後者では２単位の区間とした。これによってＢスプライン関数は、２単位区間用の関数と４単位区間用の関数の２種類できることになる。

　区間［０，２パイ］の０境界と２パイ境界では、節点が多重化するので、境界近くでは１個の２次式片のＢスプラインと２個の２次式片を連結したＢスプラインとが現れる。このため、３個の２次式片を連結した上記のＢスプライン関数の配列の規則性が失われる。区間［０，２パイ］でこの規則性を保持するために、境界附近のＢスプラインを設けるために、両端に余分な５単位の領域を追加し、区間を［０－５単位，２パイ＋５単位］とした。

　３連結のＢスプライン関数は、その中点に関して対称関数である。また、花びら山と花びら谷のスプライン曲線も各々その中点に関して対称であればよい。従って、Ｂスプライン関数の両端の２次式片のＢスプライン係数は等しくなる。そうすると、Ｂスプライン係数を求めるための連立方程式は、２単位区間用のＢスプラインの線形結合式と４単位区間用のＢスプラインの線形結合式の２式だけとなり、未知の係数は２個となり、係数の算出は容易である。

　Ｂスプライン曲線を１単位について１０個の点列で表現することにすると、計算に関与する区間は［－５０，３５０］であり、Ｅｘｃｅｌでは１つずつ加算する整数の連続データを生成すればよい。そうすると、偏角ｔは、各整数＊ＰＩ（）／１５０で表せる。

　動径ｒはｔの関数となり、３個のＢスプラインの線形結合式で表現する。各区間の最初の整数に対応してｒの計算式を設定し、この計算式をその区間の最後のｒまでコピーする。

　このようにして、各区間についてｒの値が計算できたら、その中点のｔについて意図したデータ値（ｒ＝６または２）になっていることを確認する。

　すべてのｒの計算ができたら、区間［０，３００］に対応するｒについて、ｘ＝ｒｃｏｓｔ，ｙ＝ｒｓｉｎｔの計算式により、（ｘ，ｙ）の値を計算する。

　図は、（ｘ，ｙ）の値を散布図としてグラフ表示したものである。



　このグラフを見ると、スプライン補間の技法を利用し、２次式のスプライン曲線によって１０点のデータから５弁の花びら図形を描けることが分かる。

　Ｅｘｃｅｌのグラフ表示では、ｘ軸の目盛間隔とｙ軸の目盛間隔が等しくなるとは限らない。このため、花びらの図形は、やや歪んだものとなった。

　参考文献
　吉本富士市著「インターネット時代の数学―スプライン」（共立出版）