Ｅｘｃｅｌで流線のグラフをつくる

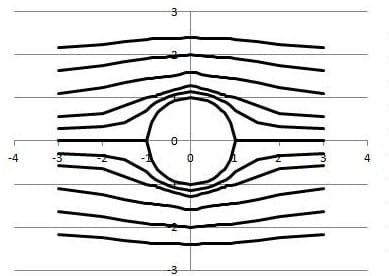
　流体力学で、一様流中に静止する円柱について、その流線を計算した。流線とは、流れのみちすじを示す曲線のことである。Ｅｘｃｅｌのグラフ機能を使って、その計算結果をグラフ表示することにした。

　流線は、ｙ＞０領域に６本、ｙ＜０領域に６本、合計１２系列つくることにし、－３＜ｘ＜３を設定する列にｘのキザミ値を入力し、各系列に計算結果のデータを入力した。円柱に沿った流線のデータを入力するために、ＥｘｃｅｌのＳＱＲＴ関数を利用した。

　今回のグラフ表示は、ブログの記事にうまくイメージを添付できるかどうかを確認するためである。

　なお、問題の流線をどのように計算するのかについては、次のブログの記事としたい。

　参考文献
　金丸隆志著「理系のためのＥｘｃｅｌグラフ入門」（ブルーバックス）

なぜ複素数が必要なのか

　中学校の数学では、２次方程式ａｘ＊＊２＋ｂｘ＋ｃ＝０の解き方が出てくる。ここでは、平方根の中の判別式ｂ＊＊２－４ａｃが負でない場合のみ解ありとし、これが負の場合には、解なしとして扱っている。

　高校の数学では、判別式が負の場合、すなわち解が複素数となる場合も解ありとし、複素平面や複素数についての簡単な演算も扱っている。

　しかし、多くの人々は、複素数という数があるな、というくらいの記憶しかなく、問題解決に複素数を利用したとう経験はほとんどないのではなかろうか。

　ｘ－ｙ座標は、例えばｙ＝ａｘ＋ｂのような式を表現するには便利であるが、物理学や工学でよく出てくる円のような回転対称な曲線を表現するには向いていない。このため、このような曲線を扱うとき、平面上の点の位置を動径ｒと偏角シータ（以下、ｔで表す）の２つの変数で表現する極座標を使うことが多い。しかし、極座標形式の数式を扱うときも、２つの変数（ｒ，ｔ）についての演算を行うときには言うまでもなく、ｒが一定で１つの変数ｔについての演算を行うときでさえ、その計算は面倒なものになりがちである。

　数式を極座標上の２つの実数の変数（ｒ，ｔ）で表現する代わりに、複素数ｚで表現すれば、１つの変数を扱うことになり、計算が楽になる場合があるのではないかという期待がもてる（もっとも、複素数ｚを用いて計算するという不安感や抵抗感のようなものを克服する必要はあるが）。複素数ｚについての演算は、多くの場合、実数ｘについての演算と同じ形式になる。

　複素数ｚをｘ－ｙ座標上の点（ｘ，ｙ）と対応させれば、ｚ＝ｘ＋ｉｙ（ｉは虚数単位）であるが、極座標上の点（ｒ，ｔ）と対応させれば、ｚ＝ｒｅｘｐ（ｉｔ）と表現できる。ｘの関数ｅｘｐ（ｘ）は、微分しても積分してもｅｘｐ（ｘ）のままという計算に便利な関数なので、ｚのｅｘｐ表現も同様のご利益にあずかれる。

　以下、複素数を利用する３つの例について説明する。

　第１の例は、電気・電子工学で交流をとり扱う方法に関するものである。

　交流電圧と交流電流を、各々、ｘ－ｙ平面上で原点Ｏのまわりに回転するベクトルとみなすことができる。電圧ベクトルの絶対値をＥ、ｘ軸からの位相角をａとすると、交流電圧は、複素数表示を用いてＥｅｘｐ（ｉａ）で表される。また、交流ベクトルの絶対値をＩ、位相角をｂとすると、交流電流は、時間変数をｔとして、Ｉｅｘｐ（ｋｔ＋ｂ）ｉのように表される。ｋは定数である。

　インダクタンスＬ、コンデンサーＣ、抵抗Ｒをもつ回路に交流電圧を印加するとき、この回路に流れる電流の時間発展は、時間に関する微分方程式で表現できる。この場合、電流、電圧を複素数表示にすると、微分や積分の答が機械的に得られ、非常に便利である。

　第２の例は、複素数ｚを変数とする複素関数ｆ（ｚ）を用いて、数式を単純化したり、演算を簡易化する方法に関するものである。
　
　まず、関数ｆ（ｚ）を用いて、実変数ｘの関数ｆ（ｘ）の定積分を行う方法について説明する。

　ｆ（ｚ）の積分については、コーシーの定理という便利な定理がある。それは、「積分路が閉じていて、その内側に被積分関数の特異点がなければ、その積分路に沿った線積分の結果は０である。」というものである。

　積分対象となる複素関数のほかに、任意の積分路を示す関数が指定されなければならない。円や直線によって閉じた積分路を指定するのが便利である。積分路が円であれば、それは変数ｚそのものを表すことになる。

　複素関数の特異点とは、以下の条件が成り立たない点である。その条件とは、その点の値が有限であり、かつその点で複素微分が可能であるという条件である。例えば、ｆ（ｚ）＝１／ｚとすると、ｚ＝０は特異点である。しかし、ｚ＝ｅｘｐ（ｉｔ）と置き換えると、ｚ＝０の特異点を避けられる。

　積分路上には特異点がないのに、なぜその内側に特異点があってはならないのか。おそらく、指定した積分路の内側にあって、この積分路から連続的に変形できる閉曲線は、すべてコーシーの定理の適用範囲であるので、結局、指定した積分路の内側にある点すべてが定理の適用範囲になるのであろう。

　以下、単純な閉曲線を例にとって、複素関数ｆ（ｚ）の定積分を求める方法を概念的に示す。

　ｘ－ｙ平面上で（－ｃ，０）から（ｃ，０）まではｘ軸上の直線であり、（ｃ，０）から（－ｃ，０）までは半径ｃの半円の円周で構成される閉曲線とする。

　複素関数ｆ（ｚ）の定積分は、
直線上でのｆ（ｚ）の定積分＋半円周上でのｆ（ｚ）の定積分＝０
である。第１項は実数の積分に他ならないから、
　　　　Ｒｌ（ｆ（ｚ））の定積分＋半円周上でのｆ（ｚ）の定積分＝０
となる。Ｒｌ（ｆ（ｚ））はｆ（ｚ）の実数部分なので、ｘの関数となる。

　従って、Ｒｌ（ｆ（ｚ））の積分は困難であるがｆ（ｚ）の積分が比較的容易な場合には、実変数関数の積分の代わりに第２項のｆ（ｚ）の積分を行えばよいことになる。

　次に、流体力学において、複素関数を巧妙に利用して演算する例を挙げる。

　流体力学において重要な変数は、直角座標（ｘ，ｙ，ｚ）における速度ベクトルｖ（ｕ，ｖ，ｗ）と圧力ｐ（ｘ，ｙ，ｚ）である。ｕ，ｖ，ｗは、各座標における速度成分である。速度ベクトルｖは、流体の流れのみちすじを示す流線のある位置の接線上にある。

　各速度成分は速度ポテンシャル関数（ｘ，ｙ，ｚ）から導かれると考えるのが便利である。この関数をｘ，ｙ，ｚで偏微分すると、各々ｕ，ｖ，ｗが得られる。速度ベクトルｖは、速度ポテンシャルの等ポテンシャル面（ｘ，ｙ，ｚ）の法線方向にあると考えればよい。これは、気象学において、低気圧や高気圧が渦なしとしたとき、等圧線の法線方向に風速ベクトルがあるのと類似している。

　以下の説明は、縮まない完全流体（粘性のない流体）の２次元の渦なし運動に関するものである。２次元の流れを考えるとき、流れの関数（ｘ，ｙ）と呼ぶ一種のポテンシャルを考えるのが便利である。流れの関数の等ポテンシャル曲線（ｘ，ｙ）を考えると、これは流線に相当するので、この曲線を横切るような流れはなく、流量は０である。速度ポテンシャル（ｘ，ｙ）が知られていなくても、流体の流量や流線の状態から流れの関数が容易に求まる場合がある。流れの関数が分かれば、それをｙおよびｘで偏微分することにより、各々ｕ，－ｖが求められる。また、両者の等ポテンシャル曲線が直交している関係から両者の関係式（コーシー・リーマンの方程式と呼ばれる）によって速度ポテンシャル（ｘ，ｙ）が計算できる。

　さらに、速度ポテンシャルを実数部、流れの関数を虚数部とする複素速度ポテンシャルｆ（ｚ）を考えることができる。すなわち、
ｆ（ｚ）＝速度ポテンシャル＋ｉ×流れの関数，　ｚ＝ｘ＋ｉｙ
である。ｆ（ｚ）をｘについて微分し、上記関係式を使うと、
ｄｆ／ｄｚ＝ｕ－ｉｖ＝ｑｅｘｐ（－ｉｔ）
が得られる。ただし、速度ベクトルの大きさをｑ、ｘ軸となす角をｔとして、
　　　　ｕ＝ｑｃｏｓｔ，　ｖ＝ｑｓｉｎｔ
の関係を用いてある。

　速度ポテンシャルあるいは流れの関数が知れている場合に速度を求めるには、微分演算をｘ，ｙについて２回行わねばならないのに対して、複素速度ポテンシャルｆを用いると、それを微分することにより、一挙に速度ベクトルが得られるのである。

　第３の例は、量子力学における複素数の利用に関するものである。

　量子力学では、複素数があると計算に便利であるという域を越えて、量子力学の基本的な方程式をつくるとき、複素数が不可欠となる。これは、２次方程式の解法を教えるとき、中学数学では何とか複素数を避けて通ったが、高校数学となると、もはや避けて通れず、複素数を扱わざるを得ないのと同様である。

　量子力学では、シュレディンガー方程式をつくるとき、物理量を演算子に置き換えている。例えば、粒子の運動量ｐを２乗した量ｐ＊＊２はマイナスの演算子に対応するから、運動量ｐに対応する演算子は、係数×ｉ×（ｄ／ｄｘ）のように、どうしても虚数ｉが現れてしまう。そうすると、方程式の解となる波動関数も、一般には複素数となる。ここで、ｄ／ｄｘは微分演算子である。

　ここで、微分演算子にも抵抗感があるかも知れない。関数ｆ（ｘ）に左から演算子ｄ／ｄｘを作用させると、それはｆ（ｘ）をｘで微分することを意味するから、微分演算子単独では単なる記号の意味しかもたないが、関数に作用させると微分結果の関数という意味あるものになる。粒子の位置など何らかの状態を定量的に表すベクトルに適当な行列を作用させると、別の状態を表すベクトルが得られるのと同様である。つまり、演算子は行列に、波動関数はベクトルに対応することになる。

　それにしても、微分演算子というのは、よくできている。微分を２回行う演算子は、（ｄ／ｄｘ）（ｄ／ｄｘ）であるが、これは、（ｄ／ｄｘ）＊＊２のことであるから、微分演算子を変数のように扱えるということであり、これが－の値に対応するのなら、ｄ／ｄｘには必然的に虚数ｉがついてくるということである。

　波動関数に複素数がついてまわろうが、そうでなかろうが、波動関数の構成要素をｃｅｘｐ（ｉｋｔ）のように複素数表示するのが便利である。波動というものはその構成要素にｃｏｓ（ｋｔ）やｓｉｎ（ｋｔ）で表される波を含むからである。これによって、波動関数に関する計算が格段に簡易化される。

　参考文献
　数学、物理学の一般的な教科書のほかに、流体力学の分野では、
　　今井功著「物理テキストシリーズ　流体力学」（岩波書店）