今年2月のブログでは、伊豆の城ヶ崎海岸の海岸線をフラクタルの数理で語ろうと試みた。
そこで、この海岸線に沿って単位線分が海岸線に乗るような折れ線を書き込み、海岸線の近似線としてフラクタル次元を計算しようとした。しかし、測定の累積誤差があまりにも大きく、使えるようなデータが得られなかった。
仕方なく、単位線分が円弧の円周に乗るような折れ線を書き込み、円周の近似線としてフラクタル次元を計算してみた。
しかし、今思うとフラクタルの専門家からは論外という評が出るだろう。フラクタルとは、自然界に見られる「不規則にゆらいでいる形や動き」を数学的に扱ったときに現れる規則性を言うのであって、円弧などはフラクタルの対象外というところであろう。
そこで、再び上記の海岸線の測定に戻ることにし、参考文献を参考にしながらボックス・カウント法と呼ばれる手法の中で曲線に適用されるデバイダー法を使って海岸線を折れ線で近似することにした。デバイダー法とは、デバイダーを使って海岸線に乗るような単位線分を順次切り出していく手法を言うのであろう。
単位線分のサイズをsとし、単位線分の数をNとするとき、デバイダー法のフラクタル次元dは、次の式によって計算できる。
d=-delta(logN)/delta(logs) (1)
deltaは隣接する2つのサンプルについて(s,N)の差分を示す。delta(logs)が負になることを予想して右辺に-をつけた。
y=logN,x=logsのような両対数座標を用いて(s,N)のサンプルの対数をとってプロットすれば、複数個のサンプルが直線y=-dx+c(cは任意の定数)上に乗るであろう。この直線は、(1)式がdを一定とする微分式とみるときの積分に相当する。
参考文献には、次のような説明がある:「自然界に現れる図形は数学的な対象物と異なり、完全な自己相似性を示すことはない。自己相似性が成立する有限の範囲が存在するので、両対数グラフへのプロットも、大きい単位線分と小さい単位線分の領域で直線からのずれが観測されることが多い。」
「自己相似性が成立する範囲」とは、べき指数が一定のべき乗則が成立する範囲と言い換えてもよいだろう。
ExcelはLOG関数を用意しているので、容易にフラクタル次元dを計算できるし、グラフを用いて(logs,logN)のプロットも容易である。
ここで対象外と考えられる円弧の円周のフラクタル次元を敢えて持ち出してみる。デバイダー法を使って円弧に内接する正方形を最初の4角形として、内接する正8,正16,正32角形のフラクタル次元を計算すると、1.129,1.029,1.009が得られる。またsを0に近づけると、dが1に収束することも明らかに推論できる。
そうすると、参考文献の説明が事実とすれば、自然界に現れる図形のうち、上記べき乗則が成立する範囲をもつ図形がフラクタル図形であり、そのような範囲をもたない図形はフラクタルではないと考えてよいのではなかろうか。有限の長さをもつ曲線がフラクタルであろうがなかろうが、sを0に近づけると、dが1に収束することは自明である。
以上のような考えは、素人考えではあるが、およそ専門家が用いそうにもないサイエンス・コミュニケーション(あるいはマス・コミュニケーション)の手法ではなかろうか。
手製のデバイダーを使って上記海岸線のs,Nを測定してみた。
複数個の(s,N)サンプルをとるとき、Nはsの単調減少関数と考えてよいだろう。そうすると、s-N座標上にサンプルをプロットしたとき、この関数のグラフからのずれが大きいサンプルを排除すればよい。
このようにして選択したサンプルについて、隣接する2つのサンプル間のフラクタル次元dを計算してみると、バラツキが大きいので愕然とする。測定結果にs測定の誤差とN測定の累積誤差が入るためかも知れない。
そこで、データが両対数グラフ上で直線性を示すか否かを観察するために、サンプルデータをグラフ表示し、近似曲線を当てはめてみた。近似曲線の当てはめには、Excelの近似曲線オプションとして線形近似と多項式近似機能が使える。Excelの近似曲線の計算には、最小二乗法を使っているという。
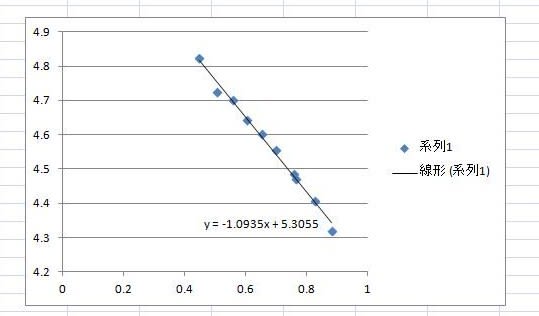
このグラフ表示をみると、データが直線性を示す可能性は示唆している。しかし、べき乗則が成立するsの範囲があるか否かについて確定できない。また、フラクタル次元dが一定であると仮定したとき、それは1.09程度であることを示している。
どうもデバイダーを使って手動で海岸線のs,Nを測定するのは時代遅れかも知れない。今では海岸線のアナログデータを入力し、ディジタルデータに変換したものにコンピュータ上のデバイダーによって単位線分を順次切り出していく手法が実施されているのであろう。このようにデバイダー法をコンピュータ・シミュレーションで実行すれば、s,Nの測定誤差が介入する余地がないのかも知れない。
(1)式は、Nがsの関数であるから、dがsによらない定数であれば、
N(s)=s^(-d) (2)
と書ける(^はべき乗を表す)。何故なら、(2)式の両辺の対数をとった後、両辺の微分をとると、(1)式になるからである。
(2)式でsからcs(cは定数)のようにスケール変換すると、
N(cs)=c^(-d)N(s)
と同じべき乗則が同じ指数に対して成立することになる。対象となる図形のスケールをc倍して関数N(s)を計算し、横軸をcsとし、縦軸をc^d倍すればN(s)と同一の曲線になる。自己相似性の別の表現である。
興味深いことは、このような指数dが対象の詳細に依存せず、同じ値となる普遍性を示すことが多くの場合に観察されることである。この指数dは考察下の現象の特徴を指定する量であり、特性指数の一つとして考えられる。
伊豆の城ヶ崎海岸のような海岸線がなぜフラクタル図形を示すのだろうか。東伊豆の海岸線は黒潮に洗われている。海の波のリズムには、べき乗則のパワースペクトルを示すゆらぎ現象が存在することが知られている。このような波のインパクトを受ける海岸線の岩石が波のゆらぎ現象を反映した構造に形成されると説明できるだろう。海岸線によって、フラクタル次元に違いが生じるのは、その地形と形成過程の違いであろうか。
参考文献
本田勝也著「フラクタル」(朝倉書店)
蔵本由紀著「非線形科学」(集英社新書)
そこで、この海岸線に沿って単位線分が海岸線に乗るような折れ線を書き込み、海岸線の近似線としてフラクタル次元を計算しようとした。しかし、測定の累積誤差があまりにも大きく、使えるようなデータが得られなかった。
仕方なく、単位線分が円弧の円周に乗るような折れ線を書き込み、円周の近似線としてフラクタル次元を計算してみた。
しかし、今思うとフラクタルの専門家からは論外という評が出るだろう。フラクタルとは、自然界に見られる「不規則にゆらいでいる形や動き」を数学的に扱ったときに現れる規則性を言うのであって、円弧などはフラクタルの対象外というところであろう。
そこで、再び上記の海岸線の測定に戻ることにし、参考文献を参考にしながらボックス・カウント法と呼ばれる手法の中で曲線に適用されるデバイダー法を使って海岸線を折れ線で近似することにした。デバイダー法とは、デバイダーを使って海岸線に乗るような単位線分を順次切り出していく手法を言うのであろう。
単位線分のサイズをsとし、単位線分の数をNとするとき、デバイダー法のフラクタル次元dは、次の式によって計算できる。
d=-delta(logN)/delta(logs) (1)
deltaは隣接する2つのサンプルについて(s,N)の差分を示す。delta(logs)が負になることを予想して右辺に-をつけた。
y=logN,x=logsのような両対数座標を用いて(s,N)のサンプルの対数をとってプロットすれば、複数個のサンプルが直線y=-dx+c(cは任意の定数)上に乗るであろう。この直線は、(1)式がdを一定とする微分式とみるときの積分に相当する。
参考文献には、次のような説明がある:「自然界に現れる図形は数学的な対象物と異なり、完全な自己相似性を示すことはない。自己相似性が成立する有限の範囲が存在するので、両対数グラフへのプロットも、大きい単位線分と小さい単位線分の領域で直線からのずれが観測されることが多い。」
「自己相似性が成立する範囲」とは、べき指数が一定のべき乗則が成立する範囲と言い換えてもよいだろう。
ExcelはLOG関数を用意しているので、容易にフラクタル次元dを計算できるし、グラフを用いて(logs,logN)のプロットも容易である。
ここで対象外と考えられる円弧の円周のフラクタル次元を敢えて持ち出してみる。デバイダー法を使って円弧に内接する正方形を最初の4角形として、内接する正8,正16,正32角形のフラクタル次元を計算すると、1.129,1.029,1.009が得られる。またsを0に近づけると、dが1に収束することも明らかに推論できる。
そうすると、参考文献の説明が事実とすれば、自然界に現れる図形のうち、上記べき乗則が成立する範囲をもつ図形がフラクタル図形であり、そのような範囲をもたない図形はフラクタルではないと考えてよいのではなかろうか。有限の長さをもつ曲線がフラクタルであろうがなかろうが、sを0に近づけると、dが1に収束することは自明である。
以上のような考えは、素人考えではあるが、およそ専門家が用いそうにもないサイエンス・コミュニケーション(あるいはマス・コミュニケーション)の手法ではなかろうか。
手製のデバイダーを使って上記海岸線のs,Nを測定してみた。
複数個の(s,N)サンプルをとるとき、Nはsの単調減少関数と考えてよいだろう。そうすると、s-N座標上にサンプルをプロットしたとき、この関数のグラフからのずれが大きいサンプルを排除すればよい。
このようにして選択したサンプルについて、隣接する2つのサンプル間のフラクタル次元dを計算してみると、バラツキが大きいので愕然とする。測定結果にs測定の誤差とN測定の累積誤差が入るためかも知れない。
そこで、データが両対数グラフ上で直線性を示すか否かを観察するために、サンプルデータをグラフ表示し、近似曲線を当てはめてみた。近似曲線の当てはめには、Excelの近似曲線オプションとして線形近似と多項式近似機能が使える。Excelの近似曲線の計算には、最小二乗法を使っているという。

このグラフ表示をみると、データが直線性を示す可能性は示唆している。しかし、べき乗則が成立するsの範囲があるか否かについて確定できない。また、フラクタル次元dが一定であると仮定したとき、それは1.09程度であることを示している。
どうもデバイダーを使って手動で海岸線のs,Nを測定するのは時代遅れかも知れない。今では海岸線のアナログデータを入力し、ディジタルデータに変換したものにコンピュータ上のデバイダーによって単位線分を順次切り出していく手法が実施されているのであろう。このようにデバイダー法をコンピュータ・シミュレーションで実行すれば、s,Nの測定誤差が介入する余地がないのかも知れない。
(1)式は、Nがsの関数であるから、dがsによらない定数であれば、
N(s)=s^(-d) (2)
と書ける(^はべき乗を表す)。何故なら、(2)式の両辺の対数をとった後、両辺の微分をとると、(1)式になるからである。
(2)式でsからcs(cは定数)のようにスケール変換すると、
N(cs)=c^(-d)N(s)
と同じべき乗則が同じ指数に対して成立することになる。対象となる図形のスケールをc倍して関数N(s)を計算し、横軸をcsとし、縦軸をc^d倍すればN(s)と同一の曲線になる。自己相似性の別の表現である。
興味深いことは、このような指数dが対象の詳細に依存せず、同じ値となる普遍性を示すことが多くの場合に観察されることである。この指数dは考察下の現象の特徴を指定する量であり、特性指数の一つとして考えられる。
伊豆の城ヶ崎海岸のような海岸線がなぜフラクタル図形を示すのだろうか。東伊豆の海岸線は黒潮に洗われている。海の波のリズムには、べき乗則のパワースペクトルを示すゆらぎ現象が存在することが知られている。このような波のインパクトを受ける海岸線の岩石が波のゆらぎ現象を反映した構造に形成されると説明できるだろう。海岸線によって、フラクタル次元に違いが生じるのは、その地形と形成過程の違いであろうか。
参考文献
本田勝也著「フラクタル」(朝倉書店)
蔵本由紀著「非線形科学」(集英社新書)









