バッハの調律法？ 自筆譜の装飾模様を巡る最近の論議

I.
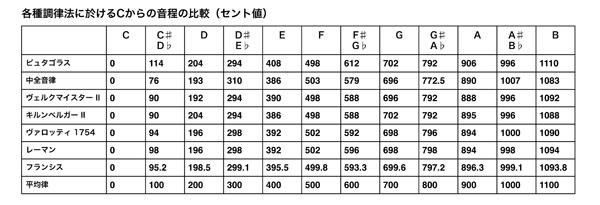
西洋の音階は、ギリシャの哲学者、ピュタゴラスが考案したとされるドとソの関係、完全5度を基本に、それを順次積み重ねることにより1オクターブ内の12の半音を導き出す調律を基本としている。しかし、完全5度を12回重ねることにより得られる嬰ロは、出発点のドとは一致せず、いくらか高くなる（これをピュタゴラスのコンマという。 コンマとは、微少な音程の差のこと）。そのため、調性によって不快な和音、いわゆる「ウルフ」が発生する。さらに、この音階によって奏する和音は、楽器の自然な倍音によって導き出される純正な和音にはならない。音楽が単旋律ではなく、多声音楽の時代になると、このことが認識され、純正な和音を得られる音階が必要になり、ルネサンスからバロックにかけて広く採用されたのが中全音律である。これは、完全5度を4回重ねて得られる長三度が、純正三度より81/80だけ広くなるので（これをシントニック・コンマという）、完全五度を1/4コンマだけ狭めて重ねて長3度を得るもので、これが1/4コンマ中全音律である。この調律法によって、多くの純正な長3度が得られた反面、ウルフが避けられなかった。18世紀に入る頃になると、さらに多くの調性が用いられるようになり、そのためウルフの解消が強く求められるようになり、様々な調律法が考案された。おびただしい数の調律法が提案されたが、その中でアンドレアス・ヴェルクマイスター（Andeas Werckmeister, 1645 - 1706） の調律法が広く採用されていた。 ヴェルクマイスターはいくつもの調律法を考案したが、基本的には中全音律の長3度の純正さを出来るだけ維持しながら、調性の自由度を広げることを目指したものであった。このような調律法を”Wohltemperierung（巧みな調律）”と名付けたのは、ヴェルクマイスターである。一方、ヨハン・ゲオルク・ナイトハルト（Johann Georg Neidhardt, 1680 - 1739）は、中全音律の枠を超えて、限りなく平均律に近づく調律法を考案した。ナイトハルトの調律法は、当時どれほど受け入れられたか不明であるが、20世紀後半になってバロックオルガンの復元に伴い採用されるようになった。18世紀の半ばになると、さらに多くの調性に適応する調律法が求められ、ゲオルク・アンドレアス・ゾルゲ（Georg Andreas Sorge, 1703 - 1778）やフリートリヒ・ヴィルヘルム・マールプルク（Friedrich Wilhelm Marburg, 1718 - 1795）等が平均律を推奨する一方で、ヨハン・フィリップ・キルンベルガー（Johann Philipp Kirnberger, 1721 - 1783）のように、「巧みな調律」の枠内で調性の自由度を広げる努力も続けられていた。
　このような状況の中で、バッハが具体的にどのような調律法を用いていたかは、自身の記述、息子達や弟子達による証言がないため全く分かっていない。バッハの調律についての記述は、「死者略伝」の中の「彼（バッハ）はチェンバロの調律に於いて、すべての調性が美しく、快く響くよう純正に、正しく調整する方法を知っていた。彼にとっては、人が不純な調律だとして避けるような調性なかったのである。（注1）」と言う記述と、ヨハン・ニコラウス・フォルケルの「ヨハン・ゼバスティアン・バッハの生涯、芸術及び芸術作品について」の中の、「また彼はチェンバロもクラヴィコードも自ら調律した。その作業は15分を越えることがなかった（注2）」というものがあるだけである。次男のカール・フィリップ・エマーヌエルがフォルケルに宛てた手紙の中で、バッハがミツラーの音楽学協会に入会したことに関連して、「故人（バッハ）は、私を始めすべての音楽家達と同様、無味乾燥な数学の類の愛好者ではありませんでした。（注3）」と書いている。
　当時のドイツ、チューリンゲン、ザクセン地方のオルガンなど音楽事情から推定すると、バッハの採用していた調律は、ヴェルクマイスターの調律法か、それに何らかの修正を加えた、中全音律を基本とする調律であったのではないかと考えられる。バッハが”Das Wohltemperierte Clavier”と言う標題を採用した背景には、ヴェルクマイスターが1681年に出版した調律法に関する本の中でこの言葉を用いていることと関連が有るのではないかと考えられている。（注4）

II.
バッハの「巧みに調律された鍵盤楽器のための前奏曲とフーガ」第1集の自筆譜表紙に、標題の文字とともにページの最上部に左右いっぱいに螺旋模様が描かれている。さらに標題の下の中央にも別の装飾が描かれている（写真参照）。これらの模様は単なる装飾と考えられており、現在でも一般的な認識は変わりない。

バッハの自筆譜の表紙のファクシミリ版：Johann Sebastian Bach, Das Wohltemperierte Clavier, VEB Deutscher Verlag für Musik Leipzig, 1971

　ところがダルムシュタット技術大学の数学者、アンドレアス・スパーシュー（Andreas Sparschuh）が1999年のドイツ数学者協会の年次会議で「J. S. バッハの巧みに調律された鍵盤楽器のための前奏曲とフーガの調律算出法（注5）」と題する発表を行い、会議の記録として刊行されたことをきっかけにして、自筆譜表紙上部の螺旋模様を、調律法を示すものとする様々な説が現れることとなった。
この模様は、両端の小さな装飾を別にすれば、螺旋形の模様が一筆で画かれている。そのうち左から3つの螺旋には、それぞれ小さな渦巻きが一つ加えられている。次の3つ（左から4個目から6個目）は単純な螺旋形、残りの6つ（左から7個目から11個目）にはそれぞれ小さな二重の渦巻きが画かれている（下の部分写真参照）。　


　すなわち螺旋模様に含まれる渦巻き模様の数は：

　　　　　　　　　　1 1 1 0 0 0 2 2 2 2 2

となる。この螺旋模様の数が11個であること、すなわち1オクターブの12の半音の間の数と同じであることと、螺旋に含まれる渦巻きの有無、1個か2個かという違いが、模様を単なる装飾ではなく、何らかの意味のあるものと考えられた理由である。
　最初にスパーシューの発表に触発されて独自の案を発表したのは、ドイツ・クラヴィコード協会の会長ミヒャエル・ザップ（Michael Zapf）で、調律の開始音は、スパーシューのAからではなくCからで、渦巻き模様一個は、完全5度から音程をずらし、それによって生ずる「うなり」が1秒に1回であることを意味すると考えた。このザップの案を含め、続出したこの螺旋模様の謎解きは、その内容に於いて多種多様で、左右両端の小さな模様を除く11個の螺旋模様を対象とするものもあれば、両端の模様も加えて13個を対象とするものもある。すなわち、左端の小さな渦を1，右端の小さな渦2つを2として：

　　　　　　　　　　1 1 1 1 0 0 0 2 2 2 2 2 2

と考える。
　また、これを記号と見る場合、それを左から読むか右から読むか、開始をAからにするか、Cからとするかなど、千差万別の読み方がされている。これらの様々な「解読」結果を発表した人の多くは数学を専攻しているか数学に通じた調律師や音楽家が多いようで、その論文は非常に難解である。
　1秒あたりの「うなり」の数との立場を取る一人、ジョン・チャールス・フランシス（John Charles Francis）は2005年に発表した論文（注6）で、両端の模様を含んだ全体の読む方向（左から右か、右から左か）、調律の方向（シャープの方向か、フラットの方向か、すなわちC-G-D-A...か、C-F-B♭-E♭...か）、出発点（12の半音のいずれか）そして、5度の循環を閉じる際の音程のずれから生ずる「うなり」の数の組み合わせ144通りをコンピューターを用いて分析して、カンマートーンとコーアトーンの音程を算出したと発表した。フランシスのカンマートーン調律法は、螺旋模様を左から右に読み、CからF、FからDと下へ5度取って行く。螺旋模様に含まれる渦1つは「うなり」が1秒に1回、渦2つが「うなり」が1秒に2回になるように調律する。そして5度の循環をGからCにおいて閉じるところで装飾模様の左端にある1つの渦巻き模様が意味を持ち、これが「うなり」が1秒に1回になることによって、調律が正しく行われたかどうか確認出来ると主張している。カンマートーンの場合は逆に、右から左に読み、CからG、GからDと上へ5度取って行く。そして5度の循環を閉じるFからCに於いて、装飾模様の右端にある2つの渦巻き模様が「うなり」2つになることを示していることになる。この1秒あたりの「うなり」の数による調律は、ミヒャエル・ザップの調律法とも共通していて、確かに調律がし易いことは確かである。この調律法における「うなり」の数は、おおよそピュタゴラス・コンマでの1/7と1/14に対応している。すなわち1秒あたり「うなり」1回が1/7ピュタゴラス・コンマ、2回が1/14ピュタゴラス・コンマに相当する。このフランシスの「解読」は、調律の容易さなどで、それなりの説得力を持っているが、ピュタゴラスの調律などほとんどの場合、CからG、GからDというように上方に5度取って行くのに対して、CからFのように下方に5度取ることや、バッハの時代には考えられない、コンピューターによる144通りもの多数の可能性からの解析によって得られたという点で、恣意的な方法に見える。またことさらにカンマートーンとコーアトーンを提示しているが、果たしてそれが必要なものであったかどうか疑問である。コーアトーンで調律されているオルガンの場合、 小型のオルガンであっても100本以上のパイプがあり、 その調律作業は簡単にできるものではない。通常は、まず製作に際してオルガンの工房で全てのパイプの調律を行い、組み立てられるもので、その後の調整も、オルガンの補修の際に行われるものであったと思われる。オルガニストが自ら行うとは考えられないのである。他のコーアトーンの楽器と言えばトランペットやホルンであるが、当時のこれらの楽器にはピストンやバルブはなく、自然倍音しか出ないので、基音以外の調整の必要はない。したがって、バッハがコーアトーンの調律法を示す必要が見あたらない。
　一方、2005年の2月号と5月号の「アーリー・ミュージック」誌に掲載されたブラッドリー・レーマンの「バッハのたぐいまれな調律法：我らのロゼッタ・ストーン」（注7）に於いては、螺旋模様を右から読んで、まずF－C－G－D－A－Eを1/6ピュタゴラス・コンマ狭く、E－B－F♯－C♯を純正に、C♯－G♯－D♯－A♯を1/12ピュタゴラス・コンマ狭く調律するという「解読」を提示した。しかし、この「解読」に当たってレーマンは、螺旋模様を右手にペンを持って書くことは通常では非常に難しいという理由で、表紙を天地逆にして書いたと考えている。その上で、天地逆にした状態で最も左の螺旋模様に接触している、天地を正常な状態にしたときにCと読める文字によって、Cの位置を示していると考え、Fを始点とすると「解読」（写真参照）した。

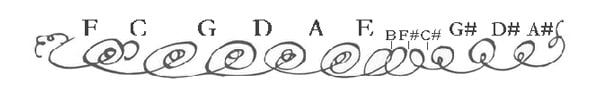
レーマンの「解読」案を示す図：Bradley Lehman, “Bach’s extraordinary temperament: our Rosetta Stone”, Early Music, Vol. XXXIII, No. 1, 2005, p. 7

まずこの螺旋模様を天地逆にすることが、突拍子もないことに思われる。バッハがこの螺旋模様だけを天地逆にして書いたとは考えられない。さらに、レーマンがCと読んだ記号（文字）だが、これは”Clavier”のCについたひげ飾りで、バッハの筆跡では他にも多くの例のある書き方であって、これがCを示す記号とは考えられない（フランシスのウェブサイトの"Other Interpretations"を参照）。その上、螺旋模様は天地逆で、Cと読んでいる記号は天地正常な状態で読むというのは、どう考えても恣意的に過ぎる。確かにこのレーマンの「解読」で提案している、1/6ピュタゴラス・コンマによる調律法は、ゲオルク・アンドレアス・ゾルゲの1758年の調律法、イタリアのヴァロッティ（1754年）、イギリスのヤング（1800年）の調律法などと共通しており、これらに調整を加えたものと言うことが出来る。しかし、これらの調律法は、何れも18世紀後半のもので、1722年よりも一世代後のものである。レーマンの論文は、イギリスの「アーリー・ミュージック」という音楽愛好家の為の雑誌に掲載されたもので、その内容は全体としてみればそれほど難解ではなく、調律の問題点や、合奏など実践的側面も取りあげていて、それなりに説得力のあるものということも出来る。しかしながら、上述したように、この調律法がバッハの「巧みに調律された鍵盤楽器のための前奏曲とフーガ」第1集の自筆譜の表紙にある装飾模様から導き出されたものだと言う根拠は、全くの虚構としか言いようがない。
　たしかにこのような装飾模様は、同じ時期に作製された他の自筆譜、「2声のインヴェンションと3声のシンフォーニア」（BWV 772 - 801, 1723年）、「無伴奏ヴァイオリンのためのソナタとパルティータ」（BWV 1001 - 1006, 1720）、ブランデンブルク辺境拍に献呈された「6曲の様々な楽器を伴う協奏曲（ブランデンブルク協奏曲）」（BWV 1046 - 1051, 1721年）、「アンナ・マグダレーナ・バッハのための音楽帳」第1集（1720年）、「ヴィルヘルム・フリーデマン・バッハのための音楽帳」（1720年）など、さらには他の時期に作製された表紙が残っている自筆譜のどれにも見られず、その特殊性が際立っていることは確かで、そこに何らかの意味があると考えたくなることも理解できる。しかし、この自筆譜表紙の長い標題の上部だけではなく下部にも装飾模様が画かれていることは、バッハがこの表紙を書くときに限って装飾を付けよう考えたに過ぎないと解釈することも出来る。


III.
以上、バッハの「巧みに調律された鍵盤楽器のための前奏曲とフーガ」第1集の自筆譜表紙に記入された螺旋模様が調律法を示すという着想を紹介した。しかし、これまでの「解読」のどれ一つをとっても、充分な根拠が欠けており、何れもまずバッハの装飾模様を調律法を示すものであるという前提があって、それに適合する調律法を様々な手段で考案し、これらをどうにかして結びつけようとする恣意的なものが感じられる。 18世紀に入って、無数の調律法が提案されていたことは前述したが、そのような時代にあって、限られた身近なものにだけ解読出来る、秘儀的な記号で調律法を記する必要があったのかどうかも大いに疑問がある。
　筆者の知る限り、バッハ研究を主としている音楽学者からはいかなる反応もないようである。これらの「解読」に関する論議は、数学者や数学に通じた音楽家達の間だけで交わされている、一種の数学的遊びではないかというのが、現在の筆者の結論である。

* John Charles Francisのウェブサイト、"Keyboard Tuning of Johann Sebastian Bach"は、この問題に関しての概要、様々な説へのリンクなど、非常に有用なサイトである。

（注1）Bach-Dokumente Band III-666
（注2）Johann Nikolaus Forkel, "Ueber Johann Sebastian Bachs Leben, Kunst und Kunstwerke", Hoffmeister und Künel, Leipzig, 1802, p. 17
（注3）Bach-Dokumente Band III-803
（注4）Andeas Werckmeister, "Orgel-Probe oder kurtze Beschreibung ... wie durch Anweiss und Hülffe des Monochordi ein Clavier wohl zu temperiren und zu stimmen sey...", Frankfurt am Main und Leipzig, 1681
（注5） Andreas Sparschuh, "Stimm-Arithmetik des wohltemperierten Klaviers",
Deutsche Mathematiker Vereinigung Jahrestagung 1999, Mainz, p.154-155,
（注6） John Charles Francis, "The Esoteric Keyboard Temperaments of J.S. Bach", 01 February, 2005 及びこの論文を数学に詳しくない音楽家や一般の音楽愛好者のために説明した"Das Wohltemperierte Clavier - Pitch, Tuning and Temperament Design"
（注7）Bradley Lehman, "Bach’s extraordinary temperament: our Rosetta Stone", Early Music, Vol. XXXIII, No. 1 and No. 2, 2005, Oxford University Press


クラシック音楽鑑賞をテーマとするブログを、ランキング形式で紹介するサイト。
興味ある人はこのアイコンをクリックしてください。