2010年に「これが----」を公開するまでは、フィンランドの数学者の代表作は下図の問題だったそうです。ある方がネットに書いておられました。「これが----」があまりにも広がったので下図は陰に隠れてしまいましたが、難易度の計算方法によっては逆転する事も有るそうです。これも最高級の難問です。

腕に自信の有る方はこれから先をご覧にならずに挑戦してみてください。理詰めで最初の数字を何処に確定させるのかは、相当な時間が必要だと思います。「U字型磁石の原則(キタムラ)」を運用すると最初の作業で一つが確定します。この原則の「物差しを使う方法」は、当初は「やっぱり同(異)種です」だけでしたが、東大の助教の問題を解くときに「どちらかは誤りです」に気が付きました。これのお陰で攻め処が増えました。ご覧の方もこの先の攻め方を是非覚えて下さい。
閑話休題 解き易くします。

進めて、

☐☐☐で7は1と同居しないので1と7は同種です。また☐☐☐で7は7-9の磁石候補となります。しかしこれはどちらかは誤りです。どちらが誤りとしても1と9は異種になります。異種は一回同居しますので1が入ります。

最初に1が確定しました。 進めて、
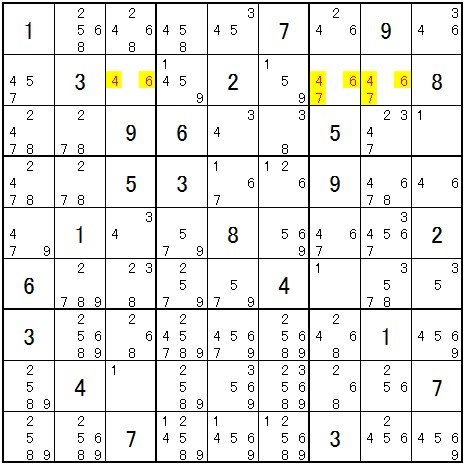
三国同盟で、

進めて、

☐で3は2と9と一回ずつ同居しますので2と9は同種です。また☐で3は9と同居しないので3と9は同種です。しかしこれはどちらかは誤りです。どちらが誤りとしても2と3は異種になります。

2と3は異種なので2または3が入ります。2が入ると2が入り、3が入ると3が入りますので、4は削除されます。。

右側ユニットで2と3は一回同居します。☐に2が5と同居しますと☐には3が入りますので5は入れません。従って2は3と5と一回ずつ同居しますので3と5は同種になります。

2は☐で9と同居しますと☐に3が入りますので、☐では3が消えて5が入ります。2は3と5と9と一回ずつ同居します。やはり3と5は同種です。従って3と5と9は同種になります。同種は同居しませんので5は削除されます。

進めて、

2と3は一回同居なので2は削除されます。

進めて、

三国同盟で、

中段ユニット☐で2と5は一回同居しますので2と5は同種です。☐に2が入りますと2と6は一回同居で2と6は異種になります。(☐には1と3が決まっていますので2と6は同時に入れません。)しかしこれはどちらかは誤りです。どちらが誤りとしても5と6は異種になります。異種は一回同居ですので6が確定します。

進めて、

さらに進めて、

二国同盟で、

進めて、

二国同盟で、 これから44連チャンが始まります。

進めて、

さらに進めて、

止まりません。

下段ユニットに迫ります。

正解です。
如何でしたか。この工程に使用したのは「どちらかは誤りです」と「やっぱり同種です」と「n国同盟」のみです。この原則を使用すれば、3数字固定の可能性の無い(消えた)ユニットであれば、仮置きをしなくても必ず攻撃することが出来ます。いままで解けなかった難問に再び挑戦してみてください。
雑記 難易度の判定基準に最後の連チャンの長さを加えるとしたら、46連チャンの「世界一----」に一票が入るでしょう。この問題は少し下なのでしょうか。
ご覧いただきまして有り難うごさいました。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます