紋様、対称性と平面充填（１）

　小学生の頃、一筆書きに興味を持って、紙やノートにいろんな一筆書きの模様を描いて楽しんでいた。その中でも、当時はその名前を知らなかったが、五芒星の形を飽かず書いていたことを思い出す。次のような星形は一筆書きが可能であった。

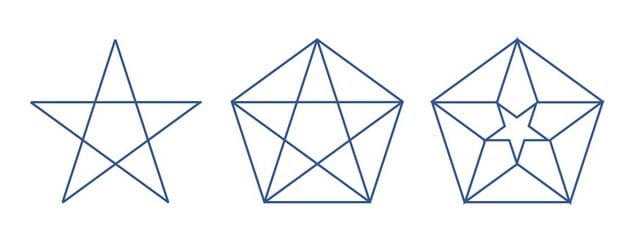
五芒星（左）と外接正五角形、星型　

　

　この五芒星はその対称性から、星型正多角形のひとつとされている。こうした子供のころからの対称性への興味からか、後年大学では金属結晶の研究をテーマに選んだ。

　大学4年生の時の研究テーマは「アルミニウム単結晶の転位構造」であった。「転位」とは結晶の乱れである。完全な単結晶であれば、現れることの無い転位構造であるが、実際にアルミニウムの単結晶をブリッジマン法で作ってみると、僅かに向きの異なる単結晶の集合体になっていることがある。その境界にはアルミニウム原子配列の僅かな乱れ＝転位が現れる。その乱れた領域がきれいなパターンを描くことがあって、これを電子顕微鏡で観察していた。

　大学院でのテーマは合金の相分離に関するもので、「スピノーダル分解」を選んだ。例えば２種類の金属からなる合金の場合、金属元素の種類にもよるが、温度により均一に混じりあうこともあれば、２相の互いに比率の異なるランダムな領域に分かれることもある。

　先ず高温で均一に混じりあった状態を作り、これを急冷して低温でも均一な状態を作った後、徐々に温度を上げていくと、その温度で安定な２相に分離していくが、その時の分離の進み方にスピノーダル分解というものがある。これを研究していた。

　卒業後の就職先には一転ガラス会社を選んだが、これは２種類の成分からなるガラスの場合にも、このスピノーダル分解が起きることを知ったからであった。

　ちょうどこの頃購入して読んでいた本に、「SYMMETRY」(HERMANN WEYL著、1952年 PRINCETON UNIVERSITY PRESS 発行)があった。また図書館で見た雑誌「数学セミナー」には伏見康治教授の「紋様の科学」が連載されていたのでこれも興味深く読んだ。

「SYMMETRY」(HERMANN WEYL著)のカバー表紙（上）と表紙（下）

　本「SYMMETRY」は今も手元にあるが、「紋様の科学」の方は、コピーをとり大切にしていたはずだが、今探してみると見当たらない。調べてみると「紋様の科学」はその後単行本として伏見康治コレクションの第1巻として発行されていることがわかり、先日上京の折に国会図書館でその内容を再読する機会をもった。この本の「解説」を見ると、「紋様の科学」は「数学セミナー」に1967年5月から1969年12月まで30回にわたって連載されたという。

伏見康治コレクション第1巻「紋様の科学」（伏見康治著　2013年、日本評論社発行）の表紙

　「SYMMETRY」では、左右対称から始まり、並進対称、回転対称などへと話が進み、古代の図案に見られる文様、幾何学図形、建築物、動植物、雪の結晶などが紹介され、最終章では鉱物結晶の数学的な側面へと話が進む。

　本の最後には、今回のブログのテーマである平面充填に関する次のようなパターンも紹介されているが、「SYMMETRY」の記述はここまでである。Weil氏は、「このような装飾文様について、できればもっと詳しく分析したい。・・・」としながらも、これ以上は触れられていない。

ムーア建築の文様（「SYMMETRY」より）

　

　

　

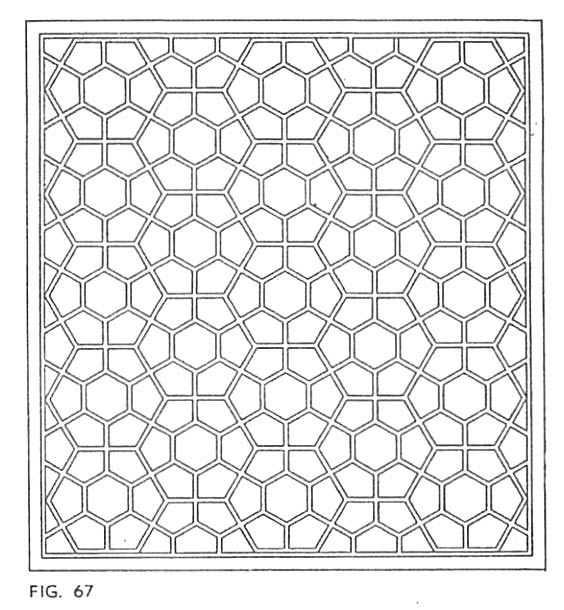
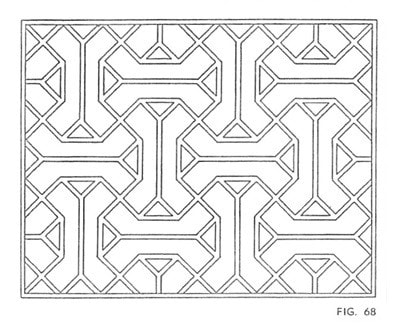
中国の窓格子文様（「SYMMETRY」より）

　「紋様の科学」にはより多くの紋様が紹介されていて、「Chapter １」は日本の「家紋」から始まっている。それは「・・・家紋とは概して対称的の形状を以て表された図象であって、・・・」という本の中での引用にもみられるように、対称的な図形に話題を導いていくものであった。

　続く「Chapter ２」は「対称操作の群」で、ここでは回転や鏡映を取り上げ、数学的な記述に移っていく。この後、様々な、紋様に関する話題が続くがこれらを一気に飛ばして、「Chapter 25 乱れ」に進むと、この章では正五角形による平面充填の話題が紹介されていて、次のように始まる。

　「正五角形についてーまんだら

　平面くり返し模様の議論を始めるそもそもの段階で、正五角形というものはその存在を否定されてしまった。結晶群論の創始者たちが、5つ割り回転対称と、周期的くり返しとが相容れないことに気がついて１，２，３，４，６の可能性を掲げたところで、正五角形の登場が禁止されてしまったように見える・・・

　さてそれはそれとして、正五角形の各辺の上に同大の正五角形を立てたのでは、その間にすき間ができて、寄せ木細工または敷石というわけにはいかない（筆者注：図B-左）。しかし、このまわりの5個の正五角形は、ひとまわり大きな正五角形に内接している点に注目しよう。・・・割れ目を無視すれば、全体の図形はやはり１つの正五角形になっているのである。それで、この『ききょう』の花のような図形と同じものを5個、その外周五角形の辺の上にたてて、もうひとまわり大きな、５つ割り対称の図形を考えることができる（同：図B-中央）。こうしてできた図形には外接五角形があり、したがってまた同じやり方で、その外側に同形同大の図形を5個ならべることができる（同：図B- 右）。等、等、等。こうした手続きの”くり返し”で平面を”おおいつくす”ことができるであろうが、その中心付近の状態は、図Cにうかがうことができる。

　”おおいつくす”ことができるといっても、もともとすきまがあることを承知の上でのことであって、上の ”くり返し” 操作のあとの段階では、このすきまも比例的に相当大きくなっていく。図Cの中で、人工衛星を連想させるような、白いすきまが、遠くになるほど大きくなって、現れている。このすきまが大きくなるのが気に入らない読者は、うすく書き込んだように、そのすきまを正五角形でうずめていただいて一向さしつかえない。うずめ方によっては、美しい星形が現れるだろう。・・・」

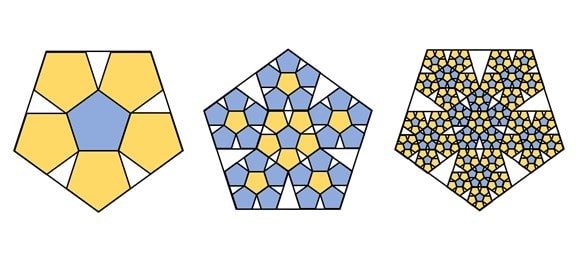
図B「紋様の科学、Chapter 25より」（筆者作成）

キキョウの蕾（左）と花に見られる５回対称性（2024.7.8 撮影）

図C　「紋様の科学、Chapter 25より」（筆者作成）

　伏見康治氏はこの後、正五角形による平面充填に関する考察を行うことについて、次のように述べている。　

　「・・・しかしこんな細工を何のためにしているのであろうか。正五角形の分子があったとせよ、そのような分子が5個の結合の手で互いにつながって、縮合して巨大な物質になったとすると、そのような物質は、けっして普通の意味で結晶にならない。つまり、何か細胞があって、その２方くり返しの形にはなっていないのである。そのような物質には、何か絶対的な中心があって、そのまわりには、5つ割り回転対称の性質があるけれども、その他の対称性はもっていない。分子の密度は全平面にわたって平均して一様にすることができるけれども、けっして並進の対称操作をもっていないのである。－－そういう不規則性の存在を示すのが目的であった。＊１」

　このページの脚注＊１には次の注記が示されている。

　「ところが、この問題をさらに追及したペンローズは、正五角形に関連したふたつの菱形で、全平面が隙間なく覆えることを発見した。」

　この脚注＊１ではふたつの菱形とされているが、ペンローズ氏が発見した5回対称を持ちながら平面を埋め尽くすことができるタイル形状すなわちペンローズ・タイルと、平面を埋め尽くす配列すなわちペンローズ・タイリングには３種類のものが知られていて、第１のもの（P1）は正五角形と３つのタイル（五芒星、ボート、ダイアモンド）からなり、第２のもの（P2）は２つの四辺形（カイト、ダート）、第３のものが２つの菱形（ファット、シン）で構成される。脚注＊１はこのうちP3のことを指しているものと思われる。

　

　ところが、上記「紋様と科学、Chapter 25」の図Cですき間を正五角形で一定のルールに従って規則正しく埋めつくしたものが、実は３種あるペンローズ・タイリングの最初のタイプP1とされるものと基本的に同一である。

　伏見康治氏の「紋様の科学 Chapter 25 乱れ」は1969年に「数学セミナー」に掲載されており、ペンローズ・タイリングP1の発見は1974年とされているので、同じような時期ではあるが、伏見康治氏はペンローズ氏よりも早く、同じような課題について考えを巡らせていたことになる。

　伏見康治氏が正五角形だけによる平面充填を意識し、正五角形以外を「すきま」と捉えていたのに対し、ペンローズ氏は「すきま」をタイルの１種と考えて、正五角形と「すきま」とをあわせた4種類のタイルで、五回対称の平面充填紋様を考えていたと言えるだろう。

　正五角形をすべて黒く塗りつぶしていた図Cを、元に戻して正五角形の色を変え、「すきま」を別の色の正五角形をで埋めると、ペンローズ・タイリングP1が現れる。

　

図Cの正五角形の配列中の２種のすきまをペンローズ・タイリングP1と同じ配列の正五角形で埋めた状態（筆者作成）

　ここで、すこし面白いことに気づく。

　伏見康治氏は最初の正五角形に始まり、次々と大きさを変えながら正五角形を周辺に拡大していくこの手法により、正五角形間の「すきま」を伴いながらも平面を無限に埋めつくすことができる配列を見出し、これが５回対称性を持ちながらも並進対称操作をもたない不規則配列であることを示した。

　ペンローズ氏の考えかたについては、直接氏の著作を読んだことがないので詳しいことは判らないが、最初の正五角形から始まり、周囲に正五角形、ダイアモンド、ボート、五芒星を厳密なルール（マッチング規則）を守りながら配列していく方法をとり、これにより５回対称性と非周期的配列とを確保しながら平面を無限に充填している。尚、正五角形については、同形状ではあるが３種類の異なるマッチング規則を与え、３種類に色分けして分類している。

　　

ペンローズ・タイリングP1（筆者作成）

　いずれにしても、完成したペンローズ・タイリングP1を見ていると、無限のバリエーションのあることが理解される。そのことは、伏見康治氏が示した「すきま」を正五角形で埋める操作を考えるとわかりやすい。次の２つの図で、最初に現れる小さい「すきま」とその次に大きい「すきま」とを正五角形で埋める２つの方法を示した。いずれもタイリング全体の５回対称と、並進対称操作を持たないという性質は保持される。

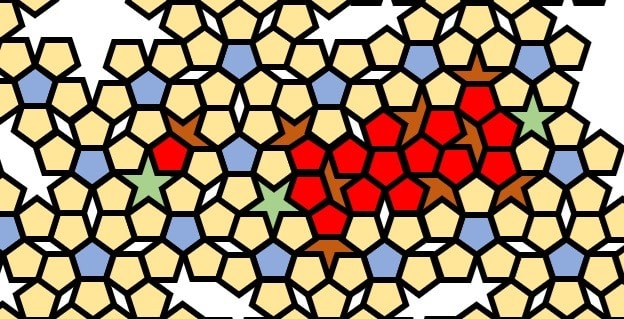
図Cの２種のすきまを正五角形で埋める方法１（筆者作成）

図Cの２種のすきまを正五角形で埋める方法２（筆者作成）

　正五角形を中心に置き、外に向かって無限に広がるこの配列の特徴は、伏見康治氏が指摘しているように、「けっして並進の対称操作をもっていない」ということである。そういう（数学的な）課題があることを、「紋様の科学」は示した。

　伏見康治氏の「すきま」のある配列がそうであるように、ペンローズ氏の「すきま」をさらに埋め尽くした配列もまた、同様に「けっして並進の対称操作をもっていない」ということになる。

　一方、正五角形による平面充填配列を考える時に、伏見康治氏が進めたように正五角形の大きさを変えながら外に向かって拡大するパターンを配列するのではなく、元の正五角形の外側に上下反転させた正五角形を一辺が接するように順に並べ、これを繰り返す方法でも、無限に外に向かって広がる充填配列を作ることができるのではないか。

　ペンローズ・タイリングP1でいえば、中心から始まる３色の正五角形の外側に正五角形を配置する時に、「ボート」を作らず「ダイヤモンド」だけを「すきま」として残しながら埋めていけば、「すきま」は大きくならず、すなわち「ボート」や「五芒星」を作ることなく、正五角形とダイヤモンド（菱形）の２種類のタイルで平面を埋め尽くすことができる。次のようである。

　

正五角形と菱形による５回対称の平面充填（筆者作成）

　両氏が共にこの単純な配列を採用しなかったのは、対称性の問題からだろうか。しかしこの配列もまた５回対称性を持ち、並進対称操作を持たないという点では変わるところがないと理解されるはずである（数学的証明はないが）。

続く