「思う壺」

ナンプレを解こうとすると、まず二択マス・強リンクを攻めようとしますが、なかなか思うように進めないですね。そのような時は三択マスを攻めますと、良い結果が出る場合が有ります。理由は色分けした場合に全て同じ色には絶対にならないからで、必ず２対１の色分けになるからです。当然同じ色の数字２個は削除されます。

 

今回の題材は、いちごナンプレ研究所 さん作の、私が「思う壺」と名付けた作品で次の図です。

　　　　　　　　

ツイッターでの最初の付与基準での難易度ポイントは１９５Ｐで、次の基準では１３３Ｐで、最新の基準では３２１Ｐの作品です。一目見て相棒ナンプレと判りますね。この作品を色々な解き方をしてみたいと思います。

　　　　　　　　

候補数字を入れます。

　　　　　　　　

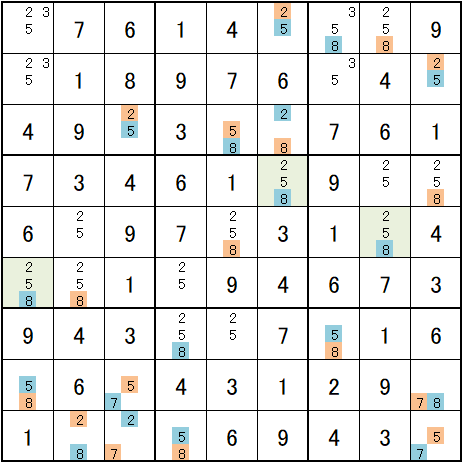
整理して、この図から解き始めます。

 

Ⅰ．Bahamut を出現させる。

 

　　　　　　　　

▢に５・８の二択マスが在ります。

　　　　　　　　

▢と▢には違う色の８が入ります。

　　　　　　　　

▢と▢のそれぞれの共通の領域である▢には８は入れませんので、削除されます。

　　　　　　　　

▢の８を８にしますと、一心同体で８が入ります。

　　　　　　　　

８を更に拡げます。

　　　　　　　　

二択マスには反対色の数字が入りますので、５が入ります。

　　　　　　　　

▢の８と▢の８は強リンクですので▢には８が入ります。▢と▢のそれぞれの共通の領域である▢には８は入れませんので削除されて、▢に８が入ります。

　　　　　　　　

▢と▢のそれぞれの共通の領域である▢に８が入ります。従って、８は削除されます。

　　　　　　　　

▢の８と▢の８は強リンクですので▢には８が入ります。

　　　　　　　　

▢と▢と▢の８のそれぞれの共通の領域である▢に８が入りますので、８は削除されます。

　　　　　　　　

８の Loop が出来ました。

　　　　　　　　

▢と▢に５・７の二択マスが有ります。

　　　　　　　　

７は一心同体ですので同じ色が入りますが、５は入れませんので７が入ります。すると、５が入りますので５は削除されます。

　　　　　　　　

▢と▢には５も５も入れませんので、削除されます。

　　　　　　　　

▢には２と５が入ります。

　　　　　　　　

３個の▢の２は一心同体ですので２が入り、二択マスですので５が入ります。

　　　　　　　　

▢には２が入りますので、５と２は削除されます。

　　　　　　　　

３個の▢には８が入ります。

　　　　　　　　

▢に２が▢に２が入りますので、３個の▢の２は削除されます。

　　　　　　　　

３個の▢には５が入ります。

　　　　　　　　

従って、５は削除されます。

　　　　　　　　

Bahamut です。２は▢のどちらかに必ず確定します。従って、▢の２は削除されます。

　　　　　　　　

削除された２は２でしたので、赤色数字は全て削除されます。２で進めて、

　　　　　　　　

５で進めて、

　　　　　　　　

７で進めて、

　　　　　　　　

８で進めて、

　　　　　　　　

３で進めて、

　　　　　　　　

正解です。この手順が一番難問らしく見えます。

 

Ⅱ．ロジックを使って普通に解く。

 

　　　　　　　　

８の奇数個連鎖です。８から下へ 強・強・強・弱・弱 で、８は削除されます。

　　　　　　　　

進めて、

　　　　　　　　

２個の▢の２は一心同体です。二択マスですので反対色の５が入ります。

　　　　　　　　

Remote Pairs です。２個の▢の２・５のそれぞれの共通の領域である▢に反対色の２・５が入ります。従って、８は削除されます。

　　　　　　　　

８で進めて、

　　　　　　　　

５で進めて、

　　　　　　　　

２で進めて、

　　　　　　　　

こちらの方が簡単に見えるでしょう。

 

Ⅲ．相棒ナンプレとして解く

 

　　　　　　　　

８の奇数個連鎖です。８から下へ 強・強・強・弱・弱 で、８は削除されます。

　　　　　　　　

８で進めて、

　　　　　　　　

相棒ナンプレではどんな問題でも中心マスには５が確定します。５で進めて、

　　　　　　　　

２で進めて、

　　　　　　　　

８で進めて、

　　　　　　　　

５で進めて、

　　　　　　　　

２で進めて、

　　　　　　　　

この作品が公開された時には相棒ナンプレと云う名称は使われていませんでしたが、点対称１０型として対応しました。

 

Ⅳ．３数字の対称性を利用して解く。

 

この手法は、numpl_nom さんが投稿して下さった手順を、ご本人の承諾を頂きまして私が自分で理解出来るよう色付けしたものです。従って、私が解いた手順ではありません。３数字の対称性を利用して解くと云う手法は初めて目にしました。

　　　　　　　　

左中ブロックの２・５・８の三択マスを▢と▢と▢に色分けをして３ヶ所に別の数字が決まるとします。

　　　　　　　　

第６行と第９行はこの色分けになります。

　　　　　　　　

第７行はこの色分けになります。

　　　　　　　　

第９列の▢は▢と▢のどちらかにになります。

　　　　　　　　

▢が▢だとすると、

　　　　　　　　

第８列はこの色分けになります。

　　　　　　　　

第３行はこの色分けになります。

　　　　　　　　

中上ブロックはこの色分けになります。

　　　　　　　　

すると、左上ブロックの３個在る▢の何処にも▢は入れません。

　　　　　　　　

つまり、▢＝▢のこの図は間違いとなります。

　　　　　　　　

▢＝▢のこの図になります。▢には同じ数字が入りますので、この時点で▢には５が入ることが判ります。

　　　　　　　　

そうすると▢には２が入ります。

　　　　　　　　

２で進めて、

　　　　　　　　

２で進めて、

　　　　　　　　

８で進めて、

　　　　　　　　

こんな手法が有るのですね。目から鱗です。numpl_nom さん有難うございました。

 

Ⅴ．究極の新手発見？その名は「あひるの子」

 

仲良し３兄弟が居るとします。稀に２人が連んで残った１人は除け者になることが有るでしょう。でもナンプレではその除け者こそが当たりなのです。童話より「あひるの子」と名付けました。

　　　　　　　　

使う数字候補は第１列だけです。▢の５・８の色分けを５・８とします。

　　　　　　　　

▢は２・５・８の三択マスです。

　　　　　　　　

▢に２が入りますと上の２マスに３・５の二国同盟が出来て、▢に８が入りますので▢の２は２です。これをＡ図とします。

　　　　　　　　

▢に５が入りますと▢に８が入りますので▢の５は５です。これをＢ図とします。

　　　　　　　　

そして、▢に８が入りますと▢に５が入りますので▢の８は８です。これをC図とします。

　　　　　　　　

Ａ図とＢ図とC図を重ねますと、▢で２と５で赤数字がダブります。

　　　　　　　　

同じマスに同じ色は複数入れませんので、赤数字は削除されます。

　　　　　　　　

この図は Ⅳ の途中図の裏返しですので、続きはご自身でどうぞ。

それと、この手法は第１列のように三択を構成している３数字とは別の数字が絡んでいることが必須で、

　　　　　　　　

第３列のような３数字だけの候補数字配置では「あひるの子」は使えませんので、ご注意ください。使えるのは、あくまでも第１列のような特殊配置の場面だけです。

 

いちごナンプレ研究所 さんの思う壺は何番目なのでしょうか。それともまだ別の手法が有るのでしょうか。

 

次回は、numpl_nom さんがコメント欄で提示された問題で、次の図です。

　　　　　　　　

コメントは、「３数字の対称性を利用して解く問題で、２方面から（すなわち二択＝色分け法）では攻略できない意味もあります。」と云うものです。

時代劇風で云えば、これは私に向けた「刺客」(笑) のようなものです。ですので、私はこの作品を「くノ 一 」と名付けました。

 

ご覧頂きまして有難うございました。