「三面張」

先日「解けないナンプレ」で検索したら、You Tube の動画に当たりまして、「超難問！こんなの解けるの？最上級ナンプレ（数独）の解き方のコツ」と云う表題でした。「数字仮定法」を使うそうです。仮定法は見ても参考にならないので、問題図のみ借用しました。投稿者さんの実力は不明ですので、難易度も不明です。ですので、ロジックを使わないで眺めて解いてみました。

 

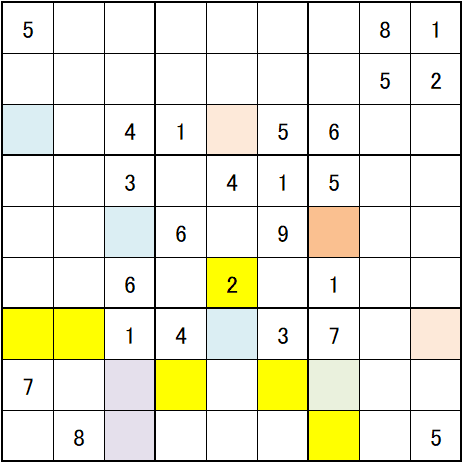
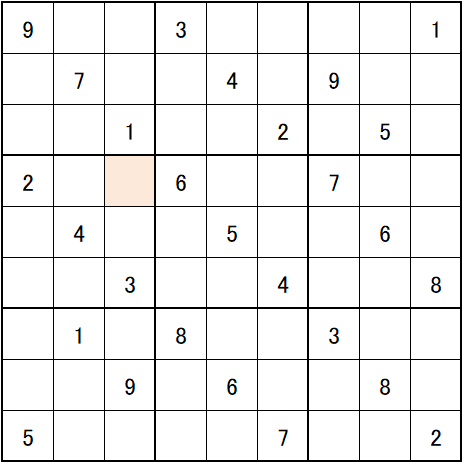
次の図が問題図です。

　　　　　　　　

私はこの問題図を「りゃん・うー・ぱー」と名付けたかったのですが、以前 いちごナンプレ研究所 さんの作品に付けさせて頂きましたので、「三面張」と名付けました。

　　　　　　　　

この問題図の急所は、上図の色付きマス４ヶ所です。

　　　　　　　　

４ヶ所の内▢が最初に二択マスになり、上図の▢の数字が確定します。

能書きはともかく解き始めます。

　　　　　　　　

３個の▢により▢の５が確定します。

　　　　　　　　

２個の▢により▢の１が確定します。

　　　　　　　　

４個の▢により▢と▢は共に３・５の二択マスになります。

余談ですが、全てのマスに候補数字を入力すると、これは中央ブロックの３個の▢は１・７・８の三国同盟になりロジックを使う事になります。

　　　　　　　　

２個の▢と▢と▢により▢の１が確定します。

　　　　　　　　

４個の▢により▢と▢は共に３・４の二択マスになります。

　　　　　　　　

この図になります。これから急所攻撃をご覧ください。

　　　　　　　　

その前に下地を、上段ユニットの２は▢と▢・▢と▢のどちらかに決まります。

　　　　　　　　

左下ブロックの６は▢と▢のどちらかに決まります。

　　　　　　　　

本番です。２個の▢により第３行の８は▢と▢のどちらかに決まります。

　　　　　　　　

２個の▢により第７行の８は▢と▢のどちらかに決まります。

　　　　　　　　

８は▢が正しいとすると第５行３列に▢が決まり、▢が正しいとすると第５行７列に▢が決まります。

　　　　　　　　

第７列の２は▢と▢と▢のどちらかに決まります。

　　　　　　　　

２が▢に決まるとすると、第７行の２個の▢は共に２・６の二択マスになります。

　　　　　　　　

すると２個の▢は共に５・９の二択マスになります。

　　　　　　　　

第３列をご覧ください。あらかじめの下地によって▢と▢には２は入れません。従って、▢に２が入ります。

　　　　　　　　

そして、２が▢に決まるとすると、第７行の２個の▢は共に２・６の二択マスになります。

　　　　　　　　

この先は、２が▢に決まった時と同じく▢に２が入ります。

　　　　　　　　

次に、２が▢に決まったら▢に８が決まります。この結果より▢は２・８の二択マスになります。

　　　　　　　　

５個の▢と１個の▢により▢に５が確定します。

　　　　　　　　

２個の▢により▢に５が確定します。

　　　　　　　　

▢により▢に５が▢に３が確定します。

　　　　　　　　

▢により▢に８が確定します。

　　　　　　　　

続いて、▢に２が確定します。

　　　　　　　　

３個の▢により▢に５が確定します。

　　　　　　　　

▢により▢に９が確定します。

　　　　　　　　

２個の▢により▢に１が確定します。

　　　　　　　　

３個の▢により▢に１が確定します。

　　　　　　　　

３個の▢により▢に２が確定します。

　　　　　　　　

２個の▢により▢に６が確定します。

　　　　　　　　

４個の▢により▢と▢に９が確定します。

　　　　　　　　

４個の▢により▢に３が▢に７が確定します。

　　　　　　　　

２個の▢により▢に７が▢に４が確定します。

　　　　　　　　

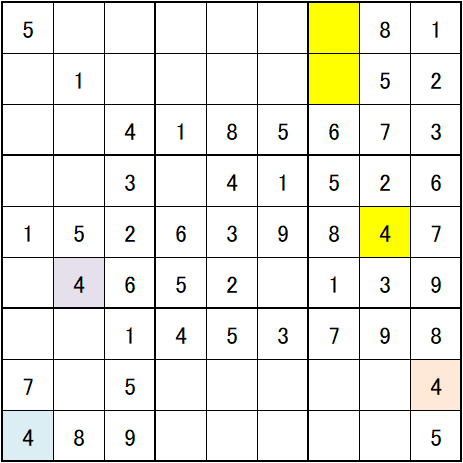
３個の▢により▢と▢と▢に４が確定します。

　　　　　　　　

続いて、▢に３が確定します。

　　　　　　　　

６個の▢により▢と▢と▢に３が確定します。

　　　　　　　　

２個の▢により▢に２が確定します。

　　　　　　　　

４個の▢により▢と▢に２が確定します。

　　　　　　　　

２個の▢により▢と▢に４が確定します。

　　　　　　　　

４個の▢により▢と▢と▢に９が確定します。

　　　　　　　　

２個の▢により▢に８が▢に７が確定します。

　　　　　　　　

▢により▢と▢と▢に６が確定します。

　　　　　　　　

２個の▢により▢と▢に２が確定します。

　　　　　　　　

▢により▢と▢と▢と▢に７が確定します。

　　　　　　　　

２個の▢により▢と▢と▢と▢に８が確定します。

　　　　　　　　

▢により▢と▢に１が確定します。

　　　　　　　　

１個マスで▢と▢に６が確定します。

　　　　　　　　

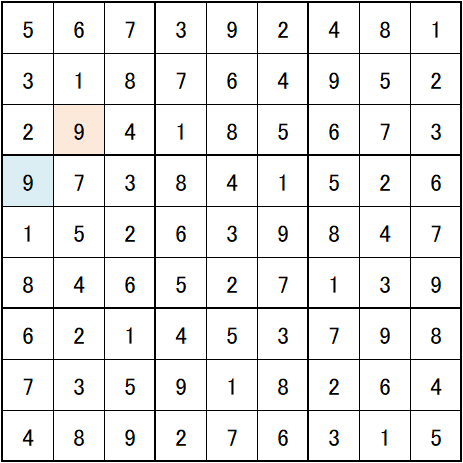
１個マスで▢と▢に９が確定します。

　　　　　　　　

正解です。

 

ご覧の通り、数字を確定させるロジックを使わず、二択マスを造る手法のみで解けました。この問題図を仮定法使用問題として嫌うとすると、作者さんが可哀想です。

 

次回は、いちごナンプレ研究所 さんの作品で、◆こんな超難問解けるわけ・・・あります。「魔法を掛けてあります」のコメントを添えてある作品で、次の図です。

　　　　　　　　

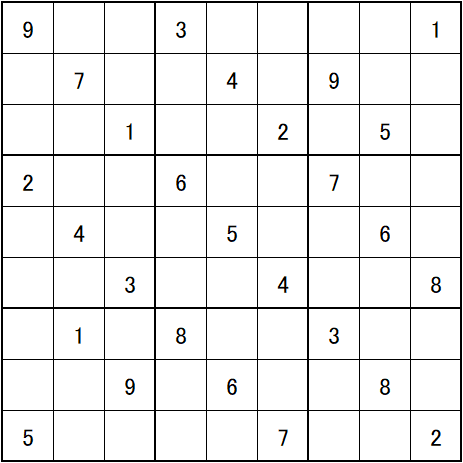
この作品は他の作品と比べて、「三色一気通貫」・「中央ブロックは魔法陣」のコメントが付いていません。何か理由があるのかもしれませんが、魔法＝魔法陣・相棒 だと思います。私はこの作品を「魔法」と名付けて通常問題として解いてみました。作家さんは超難問と謳っていますので、解けて「よかったね」と上等兵さんにはヒントを。

　　　　　　　　

魔法も仮定法も無しで、▢が一番先に確定します。すると、五合目を過ぎて後はそんなに難しくは有りません。

 

ご覧頂きまして有難うございました。