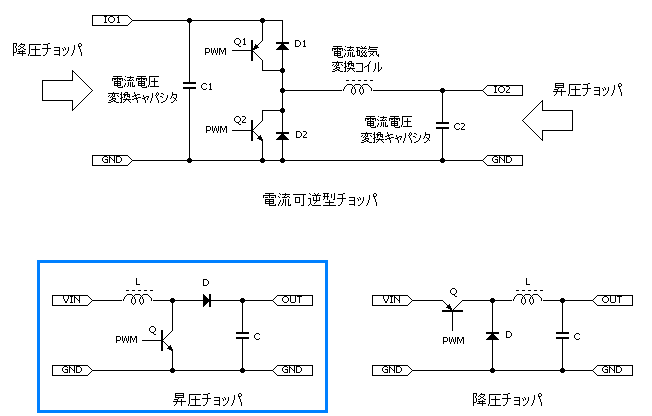
昇圧チョッパ 降圧チョッパ 双方向DC/DC（電流可逆型チョッパ）②

【昇圧チョッパ】
「昇圧チョッパ」の図を見てください。トランジスタをOFF にして、VIN に5V を入力すると出力OUT はどうなるでしょう。電流がコイルL とダイオードD を通ってコンデンサC に流れ込み、Cの端子電圧（出力OUT）が時間とともに上昇していくと想像されると思います。事実その通りで間違いはありません。

では何故C の端子電圧は「いきなり」ではなく、「徐々」に上昇するのでしょう。厳密にこれを考えればかなり難しいのですが、とりあえずは大雑把にやって、その後厳密に行きましょう。概念的に言えば、コイルに電圧を与えると電流がゼロから徐々に増加し、コンデンサに電流が流れると徐々に端子電圧が増加していくのです。つまりコイルもコンデンサも共に「徐々」に貢献しているわけですね。

これを少し学術的に表してみましょう。

【コイルLとコンデンサC】
コイルL の端子電圧をV、流れる電流をI とすると、I は次式になります。
I = 1/L∫V dt　------①

もしV が一定値の場合は
I = V/L t　（1次関数）です。I は徐々に増えますね。

コンデンサC に流れる電流をI、端子電圧をV とすると、V は次式になります。
V = 1/C∫I dt　-----②

もしI が一定の場合は
V = I/C t　（1次関数）です。V は徐々に増えますね。

さて前置きが長くなりそうな気配ですがもう少し我慢してください。チョッパ回路やDC/DC コンバータを理解するためには、頑張ってここを通るのが早道なのです。

【磁気と電気のエネルギ】
コイルの式①より
LI = ∫V dt　この両辺を記号Φで表わして
Φ= LI　また　Φ=∫V dt

コンデンサの式②より
CV =∫I dt　この両辺を記号Q で表わして
Q = CV　また　Q =∫I dt

さてΦとは、またQ とは何でしょう。Φは「磁気量（磁荷）」であり、Q は「電気量（電荷）」です。磁気量も電気量もエネルギですから、Φは容器L に溜められた「磁気エネルギ」であり、Q は容器C に溜められた「電気エネルギ」ということです。

（エネルギ量は E = 1/2 ΦI ［Ws］　E = 1/2 QV ［Ws］です）

【早くも結論】
はい。ここでもう結論を言ってしまいましょう。昇圧であれ降圧であれ、非絶縁であれ絶縁型であれ、すべてのDC/DC コンバータは「入力電力を使ってコイルL に磁気エネルギを溜め、それをコンデンサC の電気エネルギに変換し、その電気エネルギ（電力）を出力している」のです。

つまり「磁気エネルギを蓄積して電気エネルギに変換する」をスイッチング毎に行い、周波数10kHz なら、それを1秒間に10000回繰り返しているわけですね。だから、DC/DC コンバータには入力部にコイルL、出力部にコンデンサC が必ず搭載されています。

【本論に復帰】
さて長らくお待たせしてしまいました。昇圧チョッパの話を続けましょう。トランジスタをOFF にして、VIN に5Vを入力すると出力電圧が徐々に上昇します。では出力OUT（コンデンサC の端子電圧）はいったいどこまで上昇するでしょう。

少なからぬ人が「入力電圧と等しい5V に達して止まる」と回答されます。しかしそれではコイルL は抵抗R と同じということになります。コイルL は磁気エネルギを溜めているはずですね、それは一体どうなるのでしょう。Φ=LI ですから、もし出力が5V になった時に電流I がゼロであればΦ=0で磁気は消滅していますが、実際はどうなのでしょう。

I = 1/L∫V dt（あるいはΦ=∫V dt）でした。電源5V の入力時はコイルL の端子間電圧V はV = 5V ですが出力電圧（C の端子電圧）の上昇に伴い低下し、出力電圧が5V に達した時点でV = 0V になります。ということは I = 1/L∫V dt ですから、その間の端子間電圧V が積分されて、コイル電流I は最大になっています。すなわち磁気エネルギΦも最大。「これは瞬時にI がゼロになるはずがない！」と直観的に思いますよね。

その通りです。コイル電流I は最大値のまま、さらにコンデンサC に流れ続けるのです。そしてC の端子電圧は5V を超えて上昇します。これがコイルに生じる磁気エネルギΦのなせる技ですが、これはコイルと磁気の関係における「自己誘導起電力」と呼ばれる作用によります。

【誘導起電力】
自己誘導起電力については、定義式とポイントのみ示しここでは詳細には触れません。コイルL に電流I が流れるときに生じる自己誘導起電力は次式で表されます。
e =－L dI /dt　［V］

このとき、コイルLの端子電圧をv とすると次式になります。
v = L dI /dt　［V］

符号が異なりますね。この互いに「逆符号」であることがポイントであり、電流I の変化を妨げる自己誘導起電力の理解において重要な点です。

【本論に復帰】
さてコイル電流I が流れ続け、C の端子電圧（出力電圧）は5V を超えて上昇しますが、いったい何Vまで上昇するでしょうか。

この時、コイルL の入力側の端子電圧は5V、出力側の端子電圧は5V+αですから、L の端子間電圧V はマイナスになっています。（電流I の流れる方向に対して逆バイアス）。電流I の式はI = 1/L∫V dt でした。よって電流I が（最大値から）減少していくことがわかります。またコンデンサC の端子電圧VはV = 1/C∫I dt でした。よって電流I が減少し、I = 0［A］になった時点でC の端子電圧（出力電圧）の上昇は止まります。またΦ= LI ですから、この時、磁気エネルギも消滅します。

LC の時定数T はT = √LC［sec］であり、充電時間と放電時間は一致します。よってコイルL の端子間電圧V が5V～0V の時間t1と、0V～－5V の時間t2は同一です。よってt1とt2における I = 1/L∫V dt の絶対値は同じです。よってt1とt2におけるコンデンサC　の端子電圧V = 1/C∫I dt の値は同一となり、結局、出力電圧（C の端子電圧）は「10V」まで上昇します。この時、コイルL の磁気エネルギは、すべてコンデンサC の電気エネルギに変換され移行しています。

そしてこの先は、もしダイオードD がなければ、コンデンサC からコイルL の方に電流I が逆流し、C の電気エネルギがL の磁気エネルギへと移行して元の状態に戻るのですが、実際にはダイオードがあるので、電気エネルギはコンデンサC に留まります。

【エンディング】
さて、トランジスタを1度もON することなく、出力電圧が入力電圧の2倍に昇圧される様子を見てきました。大変お疲れ様でした。ここまでの話で、「昇圧チョッパ」の説明をほぼ終えたに等しいのですが、せっかくスイッチングトランジスタQ があるのだから、付録としてこいつも動かしてやりましょう。

いま出力電圧は10Vになっています。そしてコイルL の電流I はゼロであり、磁気エネルギΦもゼロです。この状態でトランジスタQ をON にします。するとコイルL に電源電圧の5Vが印加され、電流I が流れ（I = V/Lt）磁気エネルギΦ（Φ= LI ）が溜まり始めます。頃合いをみてトランジスタをOFF すると、電流I はダイオードD の方に向きを変えて流れ、コンデンサC をチャージし、出力電圧OUT は10V+α［V］になります。このトランジスタのスイッチングを継続するとどうなるでしょう。+α［V］は果てしなく大きくなっていきますね。これがチョッパ（スイッチング）による「昇圧の原理」です。

【定電圧出力】
DC/DC コンバータの出力には必ず負荷が接続され電流を食います。そもそも負荷を接続しないのであればDC/DC コンバータの存在意味はありません。よって「昇圧チョッパ」も必ず負荷を接続して考えます。スイッチングによって昇圧した出力電圧は負荷に電流が流れることによって低下します。例えばDC24V の定電圧を出力する昇圧チョッパとするためには、負荷が電流を食うことによる電圧の低下分を補うように、スイッチング回数を増やします。また負荷が食う電流量が小さくなれば出力電圧は上がろうとするので、即座にスイッチング回数を減らします。このようにして出力電圧を24V に保つことができるのです。

DC/DC コンバータの実際のスイッチング周波数は数10kHz～数100kHz ですが、上記のような負荷変動に対してはスイッチング周波数を変えるのではなく、デューティ比を変えて対応します。つまり負荷電流が大きい場合はトランジスタのON 時間を長くし、負荷電流が小さい場合はON 時間を短くするということですね。これをPWM 制御といいます。

関連記事：
「昇圧チョッパ　降圧チョッパ　双方向DC/DC（電流可逆型チョッパ）③　2012-09-10」
「昇圧チョッパ　降圧チョッパ　双方向DC/DC（電流可逆型チョッパ）①　2012-09-09」
磁界Hと磁束φ、電流Iと巻数N　2012-09-27