難易度は分かりませんが、フィンランドの数学者が2006年に公開した10作品のうち第9番目が今回の題材です。最初の問題が最難問だと本人が述べていますが。次の図が第9番「第九」です。

解き易くします。

進めて、

左側ユニットで、☐には3と7が決まっています。9が☐☐に入りますと5と一回同居で、9と5は異種です。また、☐に9が入りますと7と同居しないので、9と7は同種です。しかしこれはどちらかは誤りです。どちらが誤りとしても5と7は同種になります。同種は同居しないので、5は削除されます。

進めて、

中段ユニットで、5と8は同居しないので同種が確定しています。4が☐に入りますと5と8と各々一回同居し、このとき4-7の磁石候補です。また、☐に4が入りますと5と同居しないので、4と5は同種です。しかしこれはどちらかは誤りです。どちらが誤りとしても7と5は異種になります。異種は一回同居するので、7が入ります。

進めて、

6が☐に入ると6-4の磁石候補となり7と9と各々一回同居で、7と9は同種です。また、☐に6が入りますと7と同居しないので、6と7は同種です。しかしこれはどちらかは誤りです。どちらが誤りとしても9と6は異種になります。

6と9は異種ですので一回同居します。6が入ると6が入り、9が入ると9が入ります。従って、1と2と3は削除されます。

☐では7と8が決まっており、☐では7と5が決まっています。4が☐☐に入ると2と同居しないので、4と2は同種です。また、☐に4が入ると7と一回同居で、4と7は異種です。しかしこれはどちらかは誤りです。どちらが誤りとしても2と7は同種になります。同種は同居しないので、2は削除されます。

進めて、

☐では7と8が決まっており、☐では7と5が決まっています。4が☐☐に入ると1と同居しないので、4と1は同種です。また、☐に4が入ると7と一回同居で、4と7は異種です。しかしこれはどちらかは誤りです。どちらが誤りとしても1と7は同種になります。同種は同居しないので、1は削除されます。

進めて、
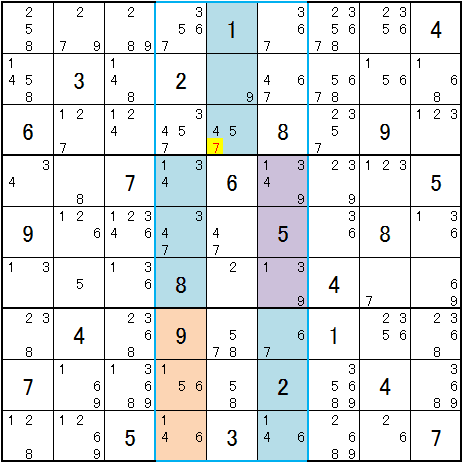
中側ユニットで、☐では5と9が決まっており、そして2と8と9は同居しないので同種です。1が☐☐に入ると9と三回同居で、1-9の磁石候補です。また、☐に1が入ると2と8と9と各々一回同居しますが、このとき1-7の磁石候補です。しかしこれはどちらかは誤りです。どちらが誤りとしても9と7は異種になります。異種は一回同居で、7が確定します。

進めて、

さらに進めて、

なおも進めて、

上段ユニットで、4と6のどちらかは必ず☐のルートに入り、一回同居しますので異種になります。

3は☐に入ると4と一回同居で3と4は異種で、このとき3と6は同種です。また、☐に3が入りますと9と一回同居で、3と9は異種です。しかしこれはどちらかは誤りで、どちらが誤りとしても4と9は異種で、6と9は同種になります。従って、6は削除されます。

進めて、

8の四辺形の原則で、8は削除されます。

6の四辺形の原則で、6は削除されます。 これで41連チャンです。

2で進めて、

8で進めて、

1で進めて、

6で進めて、

9で進めて、

3で進めて、終わりまで。

正解です。
四辺形の原則の2連続で仕上がりました。
次回は第3番目の「英雄」です。

難しいですが挑戦してみて下さい。
ご覧頂きまして有り難うございました。









