この記事は臨時です。
ラムダさんから「一心同体の二択が使えない」とのコメントが有りまして、その図を送って頂きました。

この図を見てビックリしました。超難問なんですけど、一心同体の多さです。

▢と▢と▢と▢に7の一心同体が有り、その片割れが3個のブロックに同居しています。

さらに驚いたことには▢に8の一心同体が、▢に3の一心同体が、▢に5の一心同体が、そして▢にも1の一心同体が有ります。これではどの組み合わせが一心同体の二択になるのか判断しようが有りません。このような場合は申し訳ありませんが他の手法を使われますようお願い致します。
お詫びとして私の解き順を、

既存のロジックだけでは解けないようなので、Bahamut を使ってみます。1・9の二択をこの様に色分けします。

▢に1が入ります。▢の1と▢の1との共通の領域である▢に1が入りますので、1は削除されます。

▢に1が入ると5が消えて、5の X-Wing が出来て5が入ります。

5の強リンクを繋げますと4と5と9は削除されます。

▢の1と▢の1との共通の領域である▢に1が入りますので、1は削除されます。すると、9が決まりますので、9で進めて、

Bahamut です。

第6行の▢の9が決まりますので、青グループは削除されます。。

1で進めて、
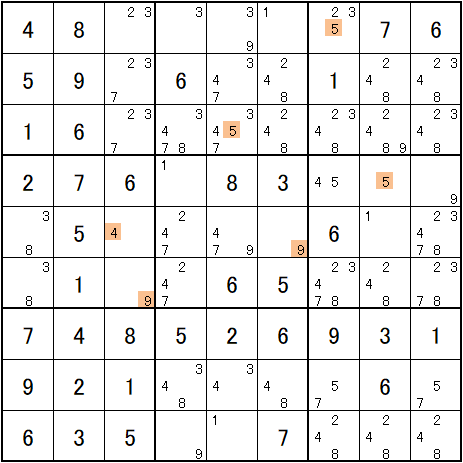
4で進めて、

5で進めて、

9で進めて、

3で進めて、

7で進めて、

4で進めて、

2で進めて、

3で進めて、
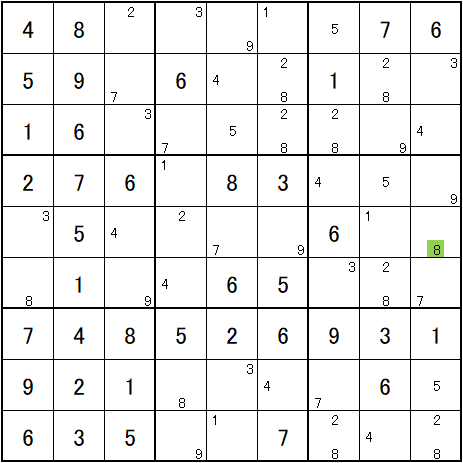
8で進めて、

正解です。
結果的には第3行4列の一心同体の二択が正しかったですが、こういう特殊な場合には「一心同体の二択」は使用なさらないでください。
ご覧頂きまして有難うございました。









