「奇数個連鎖の原則」をマスターして下さいと記述しているのに、詳細は他の方のHPをご覧くださいと云うのは、無責任だと思いますので、今回はいろいろなパターンをお見せします。
奇数個ですので、5個・7個です。9個以上は殆んど有りません。この内7個の場合を図で解説します。
まず、行・列・ブロックに同じ数字が何個入っているか調べます。2個の場合を強リンク、3個以上を弱リンクと呼び、強と弱の組み合わせで確定する場所や削除する場所が決まります。解説図として「三手詰め」の連鎖を使用します。

この図です。
Ⅰ.強・強・強・強・強・強・弱の場合 (起点を5とします。以下も同じです。)

5に決めるとすると、5と5と5も決まりますので、ブロックに5と5が同居します。矛盾が生じますので、5も5も入れません。従って、☐の5が確定します。この場合では当然ですが、5と5と5も決まります。

☐の5がここでも☐の5が確定します。
Ⅱ.強・強・強・強・強・弱・弱の場合

5に決めるとすると、5が決まりますので、☐の5または5が候補ですが、5は5が入っているので入れません。また、5に決めるとすると、5が入りますので、やはり5は入れません。従って、5は削除されます。
Ⅲ.強・強・強・強・弱・強・弱の場合

5に決めるとすると、5が決まります。そうすると5も5も入れませんので矛盾が生じます。従って、5と5が確定します。
Ⅳ.強・強・強・弱・強・強・弱の場合
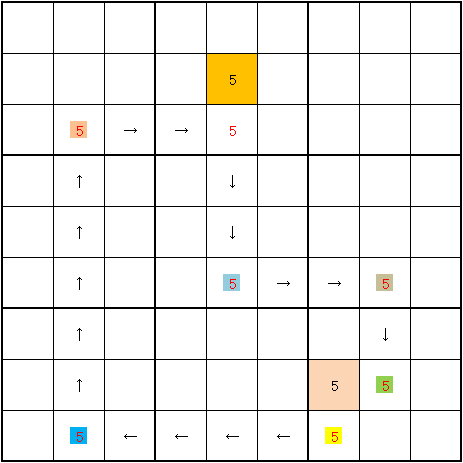
5に決めるとすると、☐の5または5が候補ですが、5に決めますと矛盾が生じますので、☐の5に決まります。そうすると5が決まります。また、5に決めますと、5と5に入りますので、やはり5が決まります。従って、5が確定します。
Ⅴ.強・強・弱・強・強・強・弱の場合
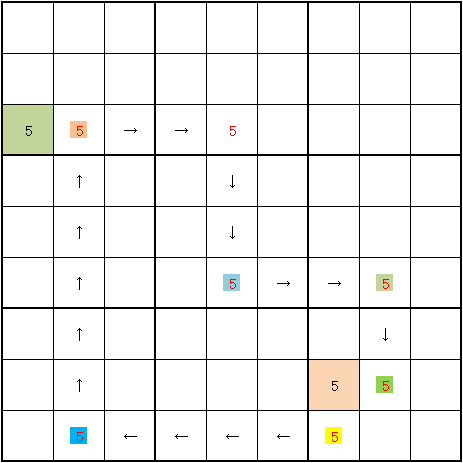
これはⅣのパターンの、起点違いです。5が確定します。
Ⅵ.強・弱・強・強・強・強・弱の場合

これはⅢのパターンの。起点違いです。5と5が確定します。
Ⅶ.強・強・強・強・弱・弱・弱の場合

このように弱リンクが三つ連続したら、奇数個連鎖にはなりません。従って、確定する数字も削除する数字も有りません。
Ⅷ.強・強・強・弱・強・弱・弱の場合

5に決めるとすると、☐の5または5が候補ですが、☐の5ですと5が決まりますので、5には入れません。5ですと、5も5も入れないので矛盾が生じます。また、5に決めるとすると、5が決まりますので、5には入れません。従って、5は削除されます。
Ⅸ.強・強・弱・強・強・弱・弱の場合

5に決めると5は入れません。また、5に決めるとすると、☐の5または5が候補です。5とすると5が決まりますので、5は入れません。しかし☐の5とすると、5が決まりますので、☐の5と5のどちらに決まるか分かりません。従って、何処の数字も確定・削除は出来ません。
Ⅹ.強・弱・強・強・強・弱・弱の場合

5に決めるとすると、5が決まりますので、☐の5または5が候補ですが、5は5が決まっていますので入れません。また、5に決めるとすると、5が決まりますので、やはり5は入れません。従って、5は削除されます。
ⅩⅠ.強・弱・強・弱・強・弱・弱の場合

5に決めるとすると、5が決まりますので、☐の5または5が候補ですが、5は5が決まっているので入れません。また、5に決めるとすると、5が決まりますので、やはり5は入れません。従って、5は削除されます。
ⅩⅡ.強・強・強・弱・弱・強・弱の場合

これはⅩのパターンの起点違いです。5が削除されます。
ⅩⅢ.強・弱・強・弱・弱・強・弱の場合

これもⅩⅠのパターンの起点違いです。5に決めるとすると5が決まりますので、5には入れません。また、5に決めるとすると、5が決まりますので、やはり5には入れません。従って、5は削除されます。
ⅩⅣ.強・弱・強・弱・強・弱・強の場合 (起点を5にすると、強・強・弱・強・弱・強・弱になります。)

☐の5・☐の5・☐の5の全てに5が入らないとすると、5と5がダブり矛盾が生じます。☐の5に決めるとすると、5が消えて5が残ります。☐の5に決めるとすると、5と5が決まります。☐の5に決めるとすると、やはり5が決まります。従って、5が確定します。
以上の他に起点違いと逆回りパターンが有ります。いろいろなパターンを覚えてください。きっとお役に経ち立ちます。ご覧になってお分かりと思いますが、Ⅸを除き二つの強に挟まれた数字が確定し、二つの弱に挟まれた数字が削除されます。
図は省略しますが、5個連鎖のパターンもお知らせします。
Ⅰ.5 強 5 強 5 強 5 強 5 弱 5 5と5が確定します。
Ⅱ.5 強 5 強 5 強 5 弱 5 弱 5 5は削除されます。 (このパターンの一つに「2 String Kite」が有ります。)
Ⅲ.5 強 5 強 5 弱 5 強 5 弱 5 5が確定します。
Ⅳ.5 強 5 弱 5 強 5 弱 5 弱 5 5は削除されます。
Ⅴ.5 強 5 強 5 弱 5 弱 5 弱 5 弱が三つ続くと確定も削除も出来ません。
この5種類で、起点違い・逆回りが有ります。
付録として、偶数個連鎖も
偶数個ですので、4個・6個・8個連鎖などです。この内4個連鎖は別名の「X-Wing」「Swordfish」「四辺形の原則」と呼ばれています。
6個以上はあまり出現しませんが、8個連鎖の「東大の助教」で解説致します。

強・弱・強・弱・強・弱・強・弱で1または1が必ず決まりますので、1は削除されます。1を確定して進めてみてください。必ず矛盾が生じます。偶数個連鎖は強と弱の繰り返しです。(但し、弱の代わりに強でも可です。)ですので、強・強と2連続した場合は偶数個連鎖に成りません。
次回からは、フィンランドの数学者が2006年に公開した10作品の中から、いくつかを紹介します。その冒頭に有る作品は、当時の最難問として「フィンランドの数学者」で記述してありますので、それをご覧ください。次回は下の図です。

私はこの作品を「運命」と名付けました。理由は5番目に載っているからです。「天才」と比べると少し緩いですが、難問ですヨ。挑戦してみてください。
ご覧頂きまして有り難うございました。









