今回は、その③。 次の問題は、地方初級（社会人）の過去問です。 4で割ると1余り、9で割ると3余るような2桁の自然数はいくつあるか。①1個②2個③3個④4個⑤5個 この場合は、N＝4a＋1＝9b＋3と立式しても、うまくまとまりません。とにかく、根性で、1つ見つけます。 4で割ると1余る自然数を、どんどん書き出します。その次に、9で割ると3余る自然数をどんどん書き出します。
共通するものはないかな？と、眺めてみると、
図に書いておきましたが、上の段は、4ずつ増加。下の段は、9ずつ増加しているので、初めに出てきた21から、36（4と9の最小公倍数）進むと、また共通する数が現れます。さらに36進むと、再び共通する数が現れますね。式で表すと、21＋36m（mは整数）となります。2桁という条件を満たすものは、m＝0（このときは21）、m＝1（このときは57）、m＝2（このときは93）の3個。よって、正解は肢③です。その1に書いていますが、もう一度繰り返すと、こうなるのです。
次回、東京消防庁1類の過去問を紹介します。
にほんブログ村
今回は、②について。 次の問題は、警察官（大卒）の過去問です。 ある3桁の整数を7、8、9で割ると、余りはそれぞれ6、7、8となる。この3桁の整数のそれぞれの位の和はいくらか。①6②8③10④12⑤14 ある整数をNとします。Nは、7で割ると6余るので、N＝7a＋6。同様に、8で割ると7余るので、N＝8b＋7。9で割ると8余るので、N＝9c＋8。まとめると、
ここで、次のことに注目します。
全部差が同じ数（この場合は1）になっています。この場合は、それぞれの辺に、その同じ数（この場合は1）を足します。
N＋1は、7の倍数かつ8の倍数かつ9の倍数ですから、504の倍数です。
よって、5＋0＋3＝8。正解は肢②です。なぜこうなるのかというと、7で割ると6余るということは、その数が、あと1だけ大きかったら、うまく7で割り切れたのに、ちょっと残念！8で割ると7余るということは、その数が、あと1だけ大きかったら、8で割り切れたのに、ちょっと残念！……ということです。次回で、パターン③を説明します。
簡単にまとめると、やり方はこうです。①引いて余りを消せ！②足して余りを消せ！③書き出せ！ 一番よく出題されるのは、②のパターンです。 とりあえず今回は、①について説明します。これは、地方初級の過去問です。 2、3、7のいずれで割っても1余る整数のうち、10以上2000以下のものは何個あるか。
題意を満たす整数をNとします。Nは、2で割ると1余るので、2a＋1（aは整数）と書きあらわすことができます。同様に、3で割ると1余るので、3b＋1、7で割ると1余るので、3c＋1とも書きあらわすことができます。
これが、引いて余りを消せ！のことです。さて、N－1は、2の倍数でもあり、3の倍数でもあり、7の倍数でもあるのだから、42の倍数です。（最小公倍数）
ということで、正解は肢②です。次回で、パターン②を説明します。
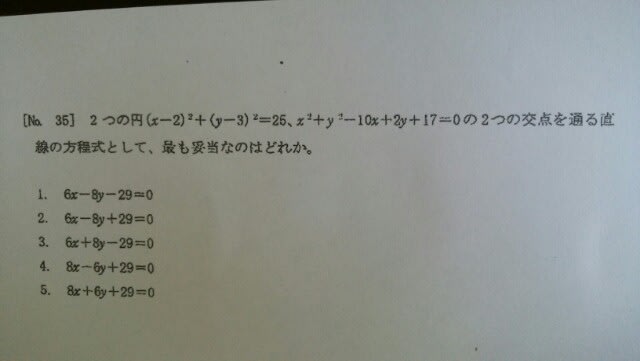円について、よく知らない場合は、この1つ前の記事をご覧下さいね。さて、円の方程式の基礎（中心の座標や、半径）を知っているだけでは、この問題は解けませんね。選択肢も使えそうにありません。この場合は、次の有名な公式を覚えておかなければいけないのです。
本問の場合は、
よって、正解は、肢①です。えっ、円①と円②を逆にしてもダイジョウブかって？もちろんダイジョウブですよ。
ほらね。しかしながら、これで納得してしまった人は、実はよくないのです。もう一度、公式をよく読んでね。「異なる2点で交わるとき」って書いてあるでしょ。これが、記述式のテストだったら、この2円が、異なる2点で交わることを、きちんと示さなければいけないのですが、選択肢から選ぶ場合は、「交わるから問題に出してるんでしょうが」と、勝手に進めてしまいましょう。では、練習問題です。これも、勝手に、異なる2点で交わるものと決めつけてやって下さいね。
です。例えば、
この方程式を、次のように変形すると、この円の中心の座標と、半径の長さがわかります。
そんなの知らなかった！とか、高校でやったけど、もう忘れてしまったという人は、次の練習問題で、少し慣れて下さいね。
解答はこうです。
そこで、平成24年5月27日の、東京消防庁1類no35ですが、これだけの知識では解けないと思います。
次回詳しく解説しますが、正解は肢①です。