練習問題②（平成25年警視庁）

A～Eの5チームが1試合ずつのバスケットボールの総当たり戦を行った。試合結果について、次のことが分かったとき、確実に言えるのはどれか。　　　　　　　　　　　　　　　　　　ア　引き分けの試合は無く、すべてのチームの勝ち数は異なっていた。　　　　　　　　　　　　　　　　　　イ　AはBに勝ったが、Cよりも勝ち数は少なかった。　　　　　　　　　　　　　　　　　　ウ　BはDに勝った。　　　　　　　　　　　　　　　　　　エ　EはCに勝った。　　　　　　　　　　　　　　　　　　①Aは2勝2敗だった。　　　　　　　　　　　　　　　　　　②BはEに勝った。　　　　　　　　　　　　　　　　　　③CはDに負けた。　　　　　　　　　　　　　　　　　　④DはAに勝った。　　　　　　　　　　　　　　　　　　⑤Eは3勝1敗だった。　　　　　　　　　　　　　　　　　　　　条件アがポイントです。全てのチームが4試合を行い、引き分けはなかったので、成績は、4勝0敗、3勝1敗、2勝2敗、1勝3敗、0勝4敗のうちのどれかになります。ところが、5人とも勝ち数が異なっていたので、この5人の成績は、4勝が1人、3勝が1人、2勝が1人、1勝が1人、0勝が1人です。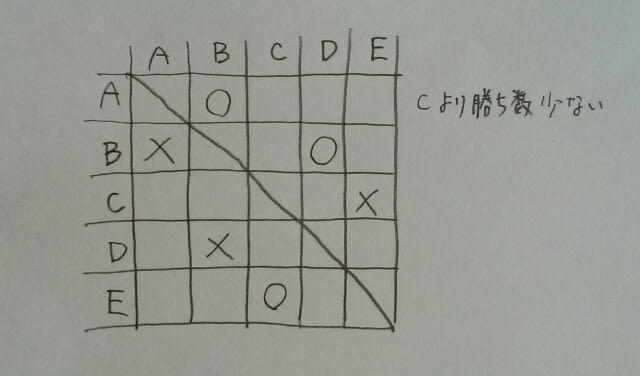4勝したのは誰でしょう？Aは、Cよりも勝ち数が少ないので、4勝ではありません。とすれば、Eですね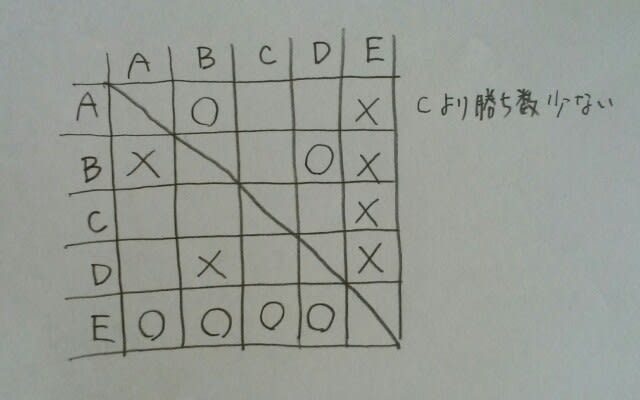！0勝だったのは誰でしょう？Cは、Aよりも勝ち数が多いので、Cではありません。とすれば、Dしかいません。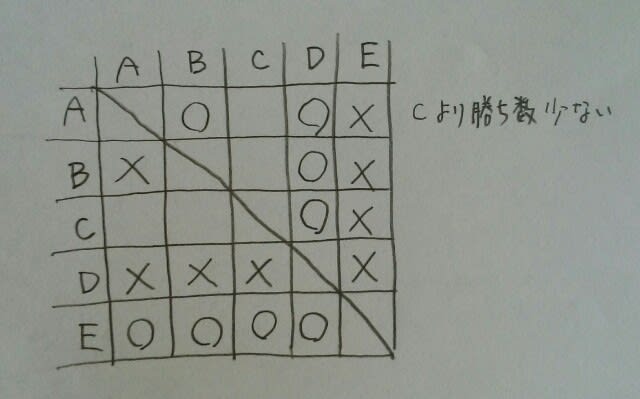この段階で、Aはすでに2勝しています。よって、Cは3勝です。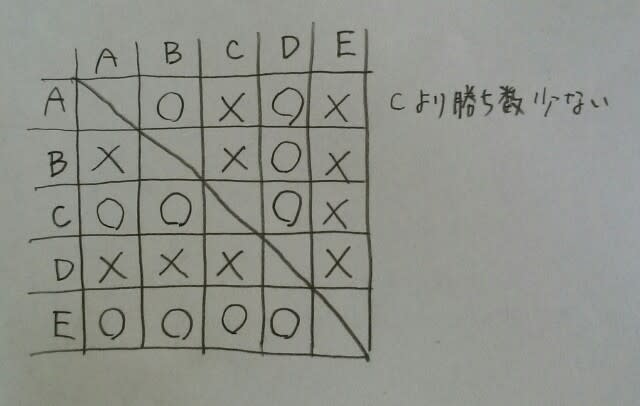選択肢と照らし合わせると、正解は、肢①です。条件のアのように、「引き分けなしで、全員違う成績」のときは、実は、リーグ戦の表は要りません。なぜなら、次の公式があるからです。これを使って、やってみると、ってなことでした。

東京消防庁1類（2017.5.28）とり急ぎやってみました。

昨日の東京消防庁1類の試験問題が手に入ったので、急いでやってみました。個人の意見なので、間違いがあるかもしれませんよ。知能分野。no7④no8⑤no9⑤no10①no11①no12②no13⑤no14②no15④no16③no17②no18④no19⑤no20⑤no21③no22④数学分野no33③no34⑤no35⑤no36⑤no37①これでいいと思うのですが！

練習問題①（平成22警察官）

雑誌読み放題サービスも選べる！【ひかりＴＶブック月額プラン】
先日の東京特別区のno10（リーグ戦）ですが、えらい難しかったと、不評でしたが、あれは、2つのパターン問題を組み合わせてあるだけで、そんなに難問ではなかったのです。いきなり解説しても、難しく感じるだけなので、順を追って説明していきます。まず、この問題はできますか？



A～Eの5人の漫才師が漫才の公演を5日間行った。毎日2人、2人、1人の3組の組をつくり、各人の相手が前回まで組んだことのある人と重なることはなかった。1日目はAとB、2日目はBとC、3日目はCとE、4日目はDとEで組んだことが分かっているとき、5日目の組み合わせとして妥当なのはどれか。 ①AとC②AとD③AとE④BとD⑤CとD 　　　　　　　　　　　　　　　　　　　　　　リーグ戦のような表を書いてみます。条件を書き込むと、（AとBが1日目に組んだので、AとBが1日目に対戦したと考えています。）（また、Aが1人で漫才をした日は、AとAが交わるところに、その数字を書き込みます。）次に、ここに注目します。ここに、「1」と記入してはいけません。なぜなら、Bは、1日目にAと組むからです。　　　　　　　　　　　　　　　　　　「2」と記入してもいけません。Bは2日目にCと組むからです。　　　　　　　　　　　　　　　　　　「3」もダメ。Bが3日目にEと組もうとしても、そのEは、Cと組んでいるからです。　　　　　　　　　　　　　　　　　　「4」もダメ。Dと組もうとしても、そのDはEと組んでいるからです。　　　　　　　　　　　　　　　　　　　よって、「5」しかありません。　　　　　　　　　　　　　　　　　　　要するに、縦と横に見て、同じ数字がダブらないようにしていけばよいのです。1、2、3、4、5を使ったパズルですね。最後までやってみて下さい。最終的に、こうなります。よつて、5日目は、AとDが組むので、正解は、肢②です。

教員採用試験教養数学（大阪府、豊能地区、大阪市、堺市）2016.7.2

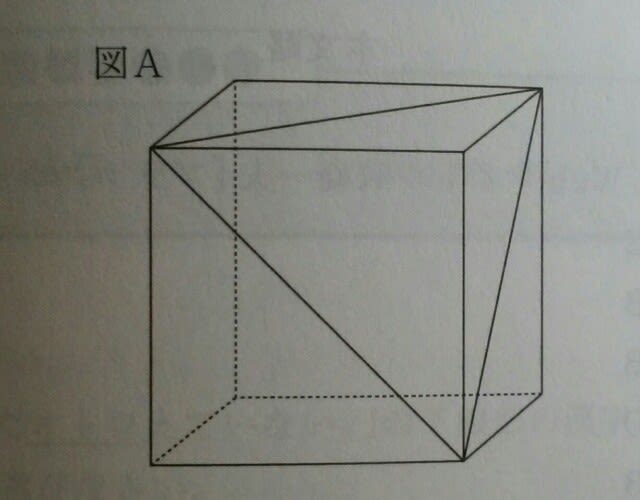
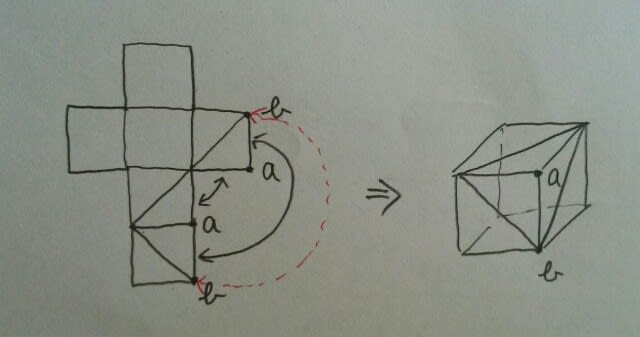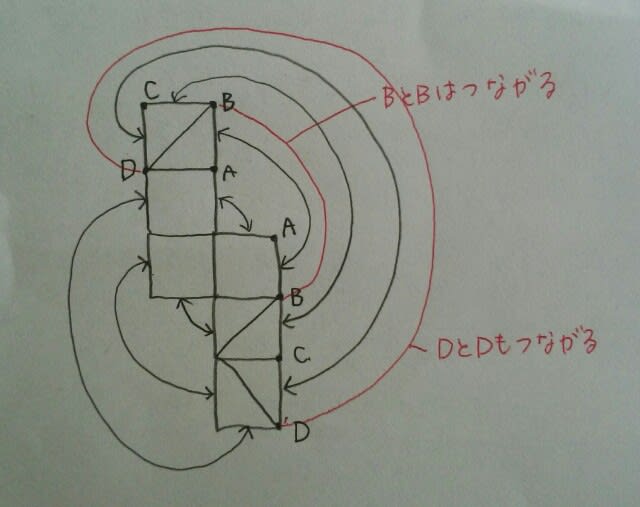次の図Aは、立方体の3つの面に対角線を引いたものである。ア～オの展開図のうち、この立方体の展開図となるもののみをすべて挙げているものはどれか。①～⑤から一つ選べ。①ア、ウ②イ、ウ③ウ、エ④イ、エ、オ⑤ウ、エ、オ　　　　　　　　　　　　　　　　　　立方体の展開図では、ある面Aと、その隣の隣にある面Bは、向かいあいます。よって、アはダメです。向かい合う面に対角線があるからです。図Aをみると、3つの対角線は、つながっています。イは、つながっていません。ウは図Aになります。エもOK。オは少し難しいですが、OKです。よって、正解は、肢⑤です。

先日の警視庁1類no34

A～Eの5人が将棋の総当たり戦を行った結果、引き分けはなく、A、B、Cの3人がそれぞれ3勝した。このとき、確実に言えることとして、最も妥当なのはどれか。　　　　　　　　　　　　　　　　　　　　①AはBに勝った。②BはDに負けた。③CはAに勝った。④DはEに勝った。⑤EはCに負けた。　　　　　　　　　　　　　　　　　　　　引き分けはなかったので、A、B、Cは3人とも3勝1敗。この3人については、それ以外何も条件がありません。なので、AとBとCは、もはや区別ができませんね。つまり、A、B、Cは、「勝ち組の3人」です。　　　　　　　　　　　　　　　　　　　　とすると、肢①と、肢③は、全く同じことを述べています。（勝ち組の誰かは、勝ち組の誰かに勝っている）肢①が確実に言えるなら、肢③も確実に言える。よって、正解は、①でも③でもありません。　　　　　　　　　　　　　　　　　　　　この総当たり戦は、全部で10試合だから、全員の戦績を合計すると、10勝10敗。勝ち組の合計が9勝3敗だから、DとEで1勝7敗。DとEは、どちらかが1勝3敗で、どちらかが0勝4敗。（DとEも、区別できません）　　　　　　　　　　　　　　　　　　　　肢②は、勝ち組の誰かは、負け組の誰かに負けたということ。仮に、BがDに負けたとすると、肢②は、あり得ない。　　　　　　　　　　　　　　　　　　　　肢④も、DとEは区別できないので、ダメです。負け組の誰かは、負け組の誰かに勝ったという内容なので、EがDに勝ったという例を作ることもできるのです。肢⑤は、負け組の人は、勝ち組の人との対戦は全て負けていることより、確実に言えます。「DはCに負けた」とか、「EはBに負けた」とか、「DはAはに負けた」という選択肢があったとしても、確実に言えます。とにかく、負け組の人は、勝ち組の人には、全敗しているのですから。