繰り上がりがあっても、足し算は得意なんですが、繰り下がりの引き算は、何か苦手です。 我々の世代の日本人は、子供の頃、塾などはほとんどなく、ソロバンとお習字が二大習い事で、ほとんど親に習わされて（？）いたものです。私もそうです。 なので、13－7は、10から7を引いたら3で、3に3を足したら6。などとは考えず、頭の中のそろばんを動かして、理屈もへったくれもなく、勝手に6になっちゃうのです。 しかし、この頭の中のそろばんは、よくバグってしまい、13－7が、7になったり、5になったりして…😰。 結論。私は繰り下がりの引き算が、大嫌いです。ついでに、分数も大嫌いです。（繰り下がりとは関係ないけど） 平成20年市役所から。 1～9の数字から3つを取り出して「ABC」と並べて3ケタの整数とする。以下の条件を満たすとき、Bの数字として考えられるものはどれか。ただし、同じ数字を2回使用することはできない。 条件1：A、B、Cの数字を並べ替えたところ、最初の数字よりも729小さくなる。 条件2：A、B、Cの数字を並べ替えて8の倍数にすることができる。 ①2 ②3 ③4 ④5 ⑤6 条件1より、 並べ替えたもの＝最初の数字－729です。恐怖の引き算です。ゆえに足し算にします。
百の位ですが、729を足したので、Aはもちろん8か9になります。0は使わないので、Aが7になることはありません。すると、次の3通りですね。
それぞれやってみます。
そして、
見事に成功！ついでに、
ということで、B＝2なので、正解は、肢①です。ここをポチッとお願いします。→
にほんブログ村
百の位ですが、729を足したので、Aはもちろん8か9になります。0は使わないので、Aが7になることはありません。すると、次の3通りですね。それぞれやってみます。そして、見事に成功！ついでに、ということで、B＝2なので、正解は、肢①です。ここをポチッとお願いします。→
にほんブログ村
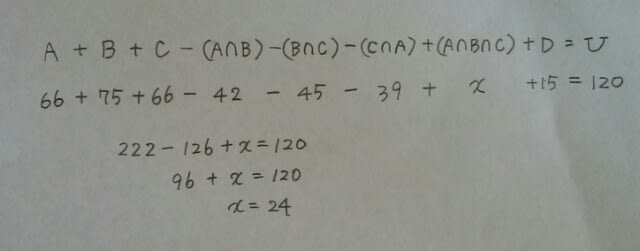よって、こうなってます。
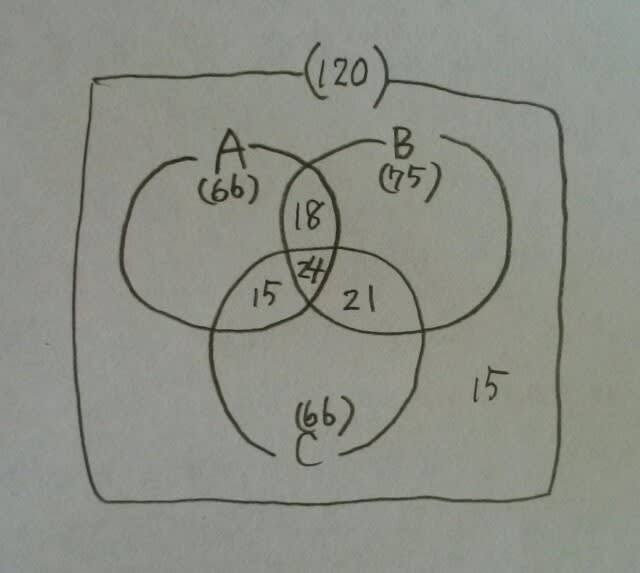一つも合格していない児童が15人。 二つだけ合格した児童は、18＋15＋21＝54人。 したがって、1曲しか合格できなかった人と3曲とも合格した人の合計は、120－15－54＝51人、正解は、肢⑤です。ここをポチッとお願いします。→
A君は、自分がX班になるかY班になるかが知りたくて、顧問の先生に聞きに行きました。 すると、顧問の先生は、「ああ、BとCはY班で、DはX班だよ。ただし、このことは、決してB、C、Dに言ってはならない。言ったら君には退部してもらうよ。はははのは！」 こんな顧問、殴ってやりたくなりますねぇ。次の問題では、さらにイヤらしくなりますよ。平成23年度国家Ⅰ種より。 A～Eの5人が、キャンプの班分けで自分がX班になるかY班になるかを知りたいと思い、担当の顧問に聞きにいった。すると顧問は、各人に対して個別に、本人と他の1人を除く3人についてのみ、X班かY班かを教えた。A～Eの各人が得た情報は次のとおりである。
その後、顧問は、A～Eが一堂に会した場で、○各人にどの3人の班を教えたかということ○Y班は多くとも3人であることの2点を伝えた。 その時点で、A～Eのだれも自分の班を特定できなかったが、そこでだれも自分の班を特定できないとわかると、まず1人だけが自分の班を特定することができた。それはだれか。①A②B③C④D⑤E そもそも、なぜこの人たちは、顧問の先生に聞きにいったのでしょうか？おそらく、X班は、近所のお粗末キャンプ場で、Y班はハワイのウッキウキキャンプ場で、自分がどっちになるか気になって仕方がなかったからです。ハワイに行けるのは多くとも3人までです。例えば、嫌みな顧問が、A君に、
と伝えたならば、A君は、もう諦めるしかありません。 A～Eの5人ともが自分の班を特定できなかったのですから、各人は、自分が教えてもらった3人が3人ともY班だったということはあり得ないのです。3人の中に必ずX班の人がいたのです。すると、A君は、こう考えます。 「BとCはハワイだなあ。EはボクとBとCのことを知っている。ボクとBとCは3人ともハワイに行くことはないのかあ。はあ？えええええ？じゃあボ、ボ、ボクは………😢」ということで、正解は、肢①でした。ここをポチッとお願いします。→
次のア～オの内容について正しいものの組合せはどれか、①～⑤から一つ選んで番号で答えなさい。 ア 1～30までの素数の和は130である。 イ ある駅では、Aのバスは8分おきに、Bのバスは12分おきに、Cのバスは18分おきに出発する。午後1時10分にA、B、Cのバスは同時に出発した。前回同時に出発した時刻は、午前11時58分である。 ウ 偶数の人数の学級の児童をA、Bの2つのチームに分ける。Aの人数が奇数のとき、Bの人数は偶数で、Aの人数が偶数のとき、Bの人数は奇数である。 エ 1～50までの整数のうち、約数が4つあるものは15個である。 オ 12、50、78、96の最小公倍数は62400で、最大公約数は2である。①ア、ウ ②イ、エ ③ア、イ、エ ④イ、エ、オ ⑤イ、ウ、オ ア……1とその数自身でしか割り切れない数を素数といいます。ただし、1は素数ではありません。よって、1～30までの素数の和は、2＋3＋5＋7＋11＋13＋17＋19＋23＋29＝129。アは誤りですね。 イ……8と12と18の最小公倍数は72。
よって、3台のバスは、72分ごとに同時に出発します。午前11時58分の72分後（1時間12分後）は、午後1時10分なので、イは正しいです。 ウ……奇数＋奇数＝偶数。奇数＋偶数＝奇数。偶数＋奇数＝奇数。偶数＋偶数＝偶数。Aが奇数でBが偶数だったら、クラスの人数は奇数人になってしまいますので、ウは誤りです。 エ……素因数分解をしたら、
となったら、この数の正の約数は、（p＋1）×（q＋1）×（r＋1）×……（個）です。なので、約数が4個になるのは、次の2パターンのみです。
よって、
1～50までの整数のうち、約数が4つあるものは、8、27、6、10、14、22、26、34、38、46、15、21、33、39、35の15個です。エは正しいです。 オ……はしご算を使う方法。
6、25、39、48の4つともを割り切ることのできる自然数は、もう1しかないので、最大公約数は2。最小公倍数を求めるときは、2つでも共通して割り切れる自然数があれば割っていき、割り切れないものは、そのまま下へ降ろします。
最小公倍数は、31200なので、オは誤りです。はしご算で最小公倍数を求めるときは、罠があります。例えば、これは罠にはまってしまった例です。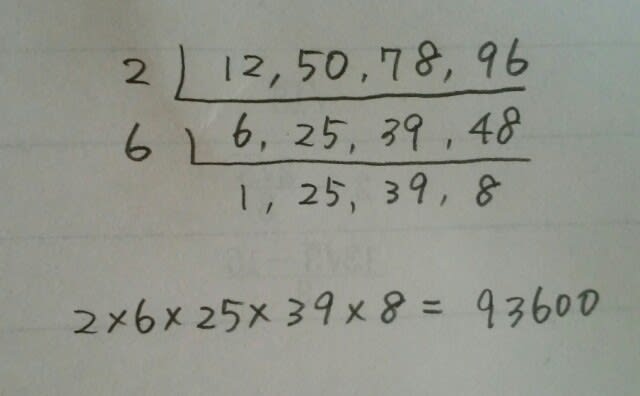
この人は、6と48は、2つとも6で割り切れるから……と考えたのですが、よく見ると、6と39と48は、3つとも3で割り切れます。つまり、共通して割り切れる数が多い方を優先して割っていかなければいけないのです。私も時々、この罠にはめられます。😵 この罠が怖いという人は、素因数分解型をお薦めします。まず確認。どんな数でも0乗すると「1」になります。逆に言うと、1は、全ての数の0乗です。やり方はこうです。
次に、0乗を使って、無理やり形を整えます。
そして、
正解は、肢②です。 ところで、このような問題では、「～ごとに」という表現は構わないのですが、「～おきに」という表現は適しません。「1日おきに診察してもらいに行く」などと言う場合、「毎日行く」ととる人もいれば、2日に1回行くととる人もいるからです。「おき」と「ごと」は、同じような意味で使われているのですが、上のように、場面によっては、その人の言語感覚によって、誤解も生じます。金輪際、この種の問題では、「おき」は使ってほしくないのですが、やっぱり今後も出て来るのでしょうねえ。😢ここをポチッとお願いします。→
「このお薬は、5倍に薄めて使用して下さい」などと言われると、「はあ？」となりませんか？ 私は、今でこそ偉そうに数学を教えていますが、子供の頃から算数や数学が全く理解できず、大学も国文学科卒です。 だって、10％を5倍にすると50％なのだから、薄めたことにはならないからです。 正確には、「このお薬は、水で量を5倍にして、そうすりゃ勝手に濃度は5分の1になるから、薄めて使用して下さい。」ですよね。 平成29年地方上級より。 次の文中のア、イに入るものがいずれも正しいのはどれか。 濃縮タイプのめんつゆA、Bがあり、Aに同量の水を加え（水で2倍に薄め）て作っためんつゆと、Bに4倍の量の水を加え（水で5倍に薄め）て作っためんつゆは、同じ濃さとなり、これが規定の濃さである。 あるとき、AとBを取り違え、Bを水で2倍に薄めて規定よりも濃いめんつゆ100mlと、Aを水で5倍に薄めて規定よりも薄いめんつゆ100mlを作ってしまった。 そこで、間違えて作っためんつゆを全て混ぜたところ、規定の濃さよりも（ ア ）なった。これに（ イ ）加えれば規定の濃さのめんつゆを作ることができる。
具体的な濃度の条件はありません。規定の濃さを10％とします。濃縮、希釈の法則より、水で量をx倍にすると、濃度はx分の1になります。Aは、水で量を2倍にすると10％になるので、20％です。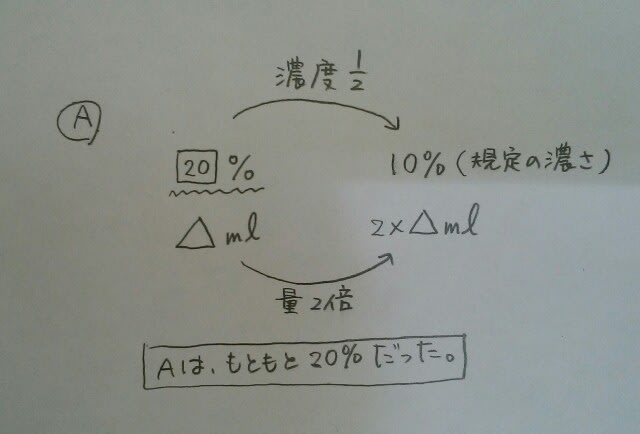
Bは、水で量を5倍にすると10％になるので、50％です。
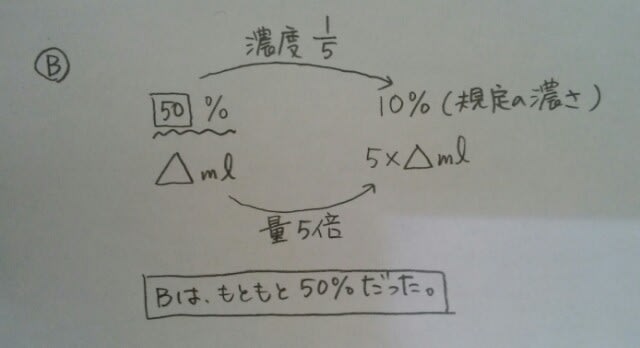そして、Bを2倍に薄めて規定よりも濃いめんつゆを100ml作ってしまったので、
Aを5倍に薄めて規定よりも薄いめんつゆ100mlを作ってしまったので、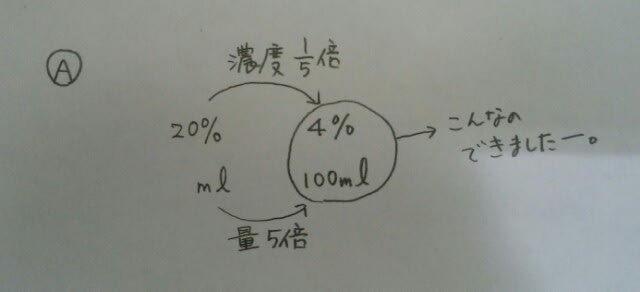
これらを全て混ぜ合わせると、（25＋4）÷2＝14.5％のめんつゆが200mlできます。（たまたま、同じ量を混ぜ合わせているので、濃度は25％と4％の真ん中になります。）よって、（ア）には、「濃く」が入ります。 これを規定の濃さの10％にするには、水で薄めるのが最適。でも、14.5％を何倍すると10％になるかは、すぐには分からないので、こんなときには、濃縮希釈の法則その2を使いましょう。
200ml→290mlより、90mlの水を加えています。イには、「水を90ml」が入ります。正解は、肢④です。 ちょっと、調べてみました。英語でも、水で～倍に薄めるというときは、dilite it ～ times with water というそうです。ドイツ語も同様です。日本語だけおかしいというわけではなく、私がおかしかっただけ？😰ここをポチッとお願いします。→