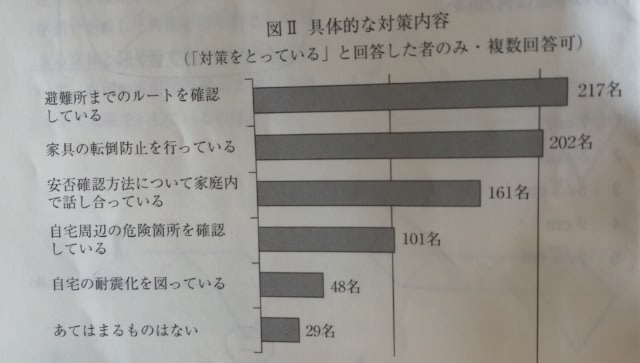
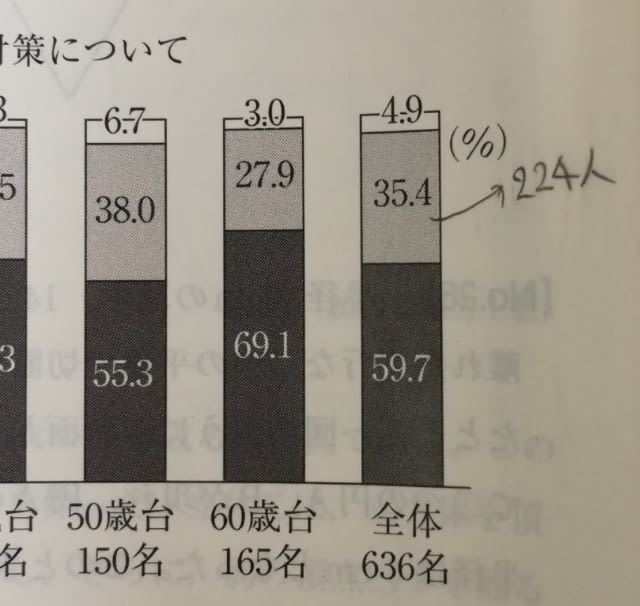
図は、日本のある産業における、アジア現地法人の日本向け販売額、現地販売額、逆輸入比率を示したものである。この図から正しく言えるのはどれか。 ただし、逆輸入比率は次の式で算出されるものである。
① 2011〜2017年のうちには、日本向け販売額は前年に比べて増加したが、逆輸入比率は前年に比べて減少した年が全部で3回ある。 ② 2010年と2017年について、日本向け販売額と現地販売額の合計を比べると、2017年は2010年の3倍を超えている。 ③ 2013年において、現地販売額の対前年増加率は、日本向け販売額の対前年増加率よりも高い。 ④ 2014年〜2017年のいずれの年も、日本向け販売額と現地販売額の合計に占める日本向け販売額の割合は25%を超えている。 ⑤ 2015年と2016年についてアジアからの輸入総額を比べると2015年の方が多い。 ①は、こんな年が3回あったかなかったかを調べるのですね。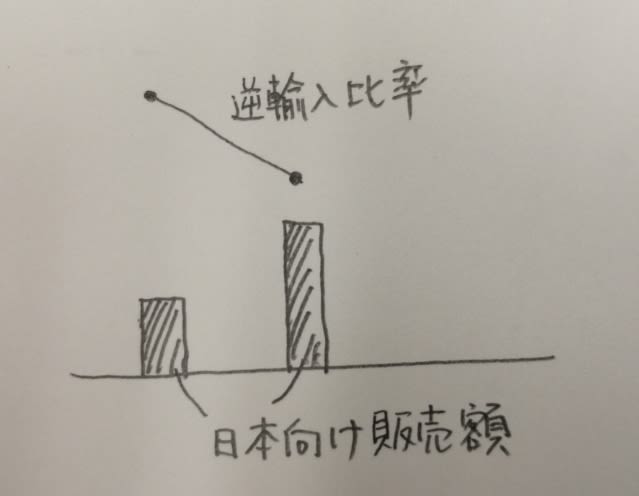
すると、2016、2017年の2回だけなので誤り〜。 ②2010年は、100+560=660。(560は、570でも580でも可)2017年は520+1300=1820。3倍には届きませんので誤り〜。 ③ 2012〜2013年にかけて、日本向け販売額は、2倍近く(100%近く)増加しているのに、現地販売額は25%程度しか増加していない様子が、グラフから見てとれます。これも誤り〜。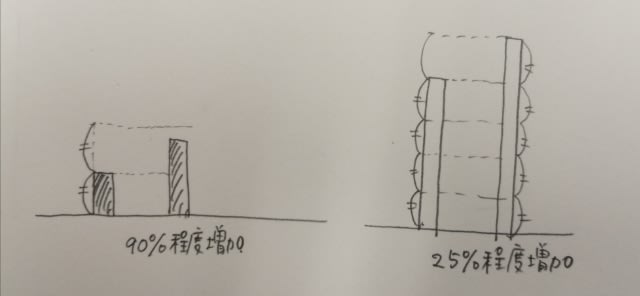
④ 日本向け販売額と現地販売額の合計に占める日本向け販売額の割合が25%であれば、こうなっています。
2013年がこの状態に近いですね。 2014〜2017年は、どの年も25%を超えているのが計算しなくてもグラフから分かります。2016年が少し微妙ですが、日本向け販売額が400、それを3倍すると1200ということから、やはり25%超えということがはっきりしますね。 ⑤ アジアからの輸入総額をxとすると、逆輸入比率の算出式より、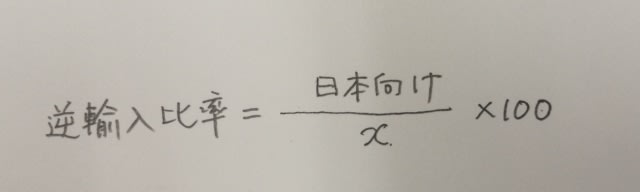
肢⑤は、どちらが大きいかを比べるだけなので、×100ってやつは、ガン無視しましょう。すると、両辺をx倍して、
2015年と2016年は、
分母が減って、分子が増えているので、計算不要です。正解は、肢④です。ここをポチッとお願いします。→
にほんブログ村


① 2011〜2017年のうちには、日本向け販売額は前年に比べて増加したが、逆輸入比率は前年に比べて減少した年が全部で3回ある。 ② 2010年と2017年について、日本向け販売額と現地販売額の合計を比べると、2017年は2010年の3倍を超えている。 ③ 2013年において、現地販売額の対前年増加率は、日本向け販売額の対前年増加率よりも高い。 ④ 2014年〜2017年のいずれの年も、日本向け販売額と現地販売額の合計に占める日本向け販売額の割合は25%を超えている。 ⑤ 2015年と2016年についてアジアからの輸入総額を比べると2015年の方が多い。 ①は、こんな年が3回あったかなかったかを調べるのですね。

すると、2016、2017年の2回だけなので誤り〜。 ②2010年は、100+560=660。(560は、570でも580でも可)2017年は520+1300=1820。3倍には届きませんので誤り〜。 ③ 2012〜2013年にかけて、日本向け販売額は、2倍近く(100%近く)増加しているのに、現地販売額は25%程度しか増加していない様子が、グラフから見てとれます。これも誤り〜。

④ 日本向け販売額と現地販売額の合計に占める日本向け販売額の割合が25%であれば、こうなっています。

2013年がこの状態に近いですね。 2014〜2017年は、どの年も25%を超えているのが計算しなくてもグラフから分かります。2016年が少し微妙ですが、日本向け販売額が400、それを3倍すると1200ということから、やはり25%超えということがはっきりしますね。 ⑤ アジアからの輸入総額をxとすると、逆輸入比率の算出式より、
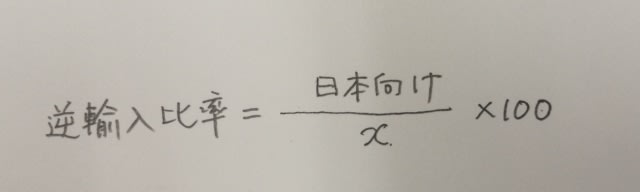
肢⑤は、どちらが大きいかを比べるだけなので、×100ってやつは、ガン無視しましょう。すると、両辺をx倍して、

2015年と2016年は、

分母が減って、分子が増えているので、計算不要です。正解は、肢④です。ここをポチッとお願いします。→
にほんブログ村