正の整数xがある。147をxで割ると余りが11となり、113をxで割っても余りが11となる。またxを13で割ると余りが8となる。ではxを15で割ったときの余りはいくらか。①3②4③5④6⑤7(平成24年大卒警察官) 例えば、15÷7を計算すると、15÷7=2余り1ですね。割り算では、次のことがいえます。 2つとも、非常に大事なことで、実は、小学校の3年生で学習していたのです。特に、②は、うっかり確認を怠ることがよくあります。15÷7=1余り8などとしてはいけませんね。本問の場合は、
2つとも、非常に大事なことで、実は、小学校の3年生で学習していたのです。特に、②は、うっかり確認を怠ることがよくあります。15÷7=1余り8などとしてはいけませんね。本問の場合は、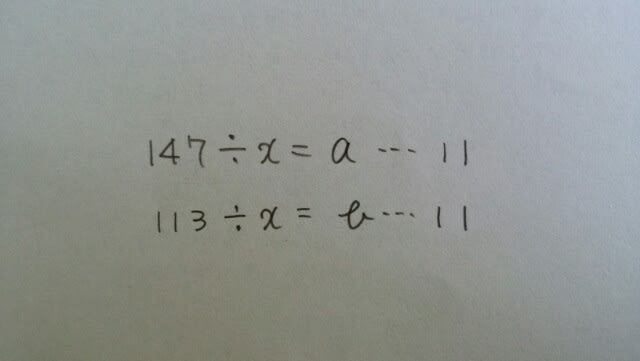 ということですから、
ということですから、 ところで、約数とは?例えば、20の正の約数をすべてみつけましょう。
ところで、約数とは?例えば、20の正の約数をすべてみつけましょう。 □や、○に入るものが、20の約数です。
□や、○に入るものが、20の約数です。 よって、20の正の約数は、1、2、4、5、10、20です。
よって、20の正の約数は、1、2、4、5、10、20です。 ということで、xは、136と102の公約数です。では、公約数ってどうやって求めるの?公約数を、全て求めるときは、まず最大公約数を求め、その最大公約数の約数を求めればいいのです。136と102の最大公約数は、
ということで、xは、136と102の公約数です。では、公約数ってどうやって求めるの?公約数を、全て求めるときは、まず最大公約数を求め、その最大公約数の約数を求めればいいのです。136と102の最大公約数は、 34ですから、その34の約数を求めます。
34ですから、その34の約数を求めます。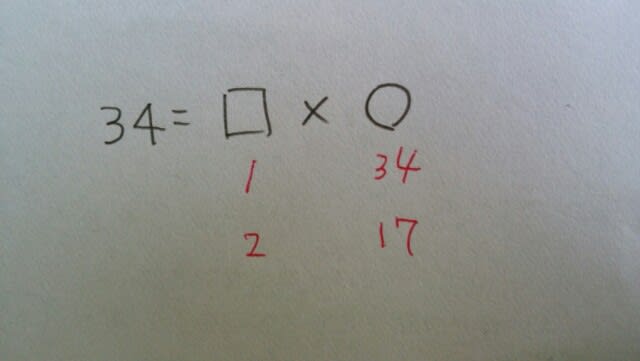 1、2、17、34です。しかし、割る数は、余りよりも大きくなければいけません(割る数>余り) xは、11よりも大きくなければいけないので、17か、34です。17だつたとすると、15で割ると余りは2。これは選択肢にはありません。34だつたとすると、15で割ると余りが4。これは肢②にあります。よって、正解は肢②です。
1、2、17、34です。しかし、割る数は、余りよりも大きくなければいけません(割る数>余り) xは、11よりも大きくなければいけないので、17か、34です。17だつたとすると、15で割ると余りは2。これは選択肢にはありません。34だつたとすると、15で割ると余りが4。これは肢②にあります。よって、正解は肢②です。
にほんブログ村

 2つとも、非常に大事なことで、実は、小学校の3年生で学習していたのです。特に、②は、うっかり確認を怠ることがよくあります。15÷7=1余り8などとしてはいけませんね。本問の場合は、
2つとも、非常に大事なことで、実は、小学校の3年生で学習していたのです。特に、②は、うっかり確認を怠ることがよくあります。15÷7=1余り8などとしてはいけませんね。本問の場合は、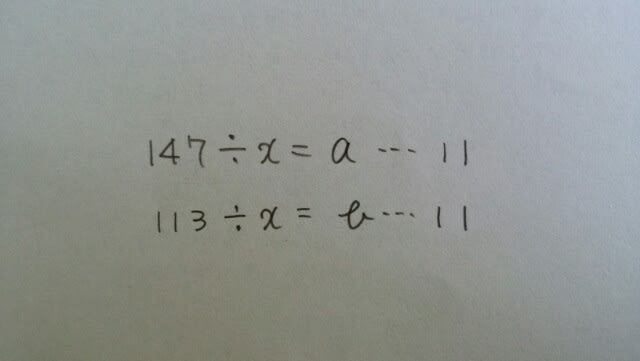 ということですから、
ということですから、 ところで、約数とは?例えば、20の正の約数をすべてみつけましょう。
ところで、約数とは?例えば、20の正の約数をすべてみつけましょう。 □や、○に入るものが、20の約数です。
□や、○に入るものが、20の約数です。 よって、20の正の約数は、1、2、4、5、10、20です。
よって、20の正の約数は、1、2、4、5、10、20です。 ということで、xは、136と102の公約数です。では、公約数ってどうやって求めるの?公約数を、全て求めるときは、まず最大公約数を求め、その最大公約数の約数を求めればいいのです。136と102の最大公約数は、
ということで、xは、136と102の公約数です。では、公約数ってどうやって求めるの?公約数を、全て求めるときは、まず最大公約数を求め、その最大公約数の約数を求めればいいのです。136と102の最大公約数は、 34ですから、その34の約数を求めます。
34ですから、その34の約数を求めます。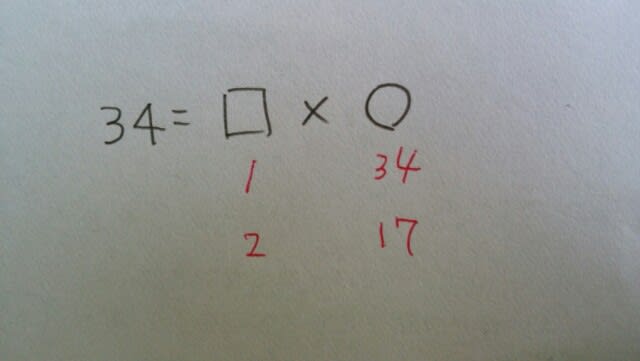 1、2、17、34です。しかし、割る数は、余りよりも大きくなければいけません(割る数>余り) xは、11よりも大きくなければいけないので、17か、34です。17だつたとすると、15で割ると余りは2。これは選択肢にはありません。34だつたとすると、15で割ると余りが4。これは肢②にあります。よって、正解は肢②です。
1、2、17、34です。しかし、割る数は、余りよりも大きくなければいけません(割る数>余り) xは、11よりも大きくなければいけないので、17か、34です。17だつたとすると、15で割ると余りは2。これは選択肢にはありません。34だつたとすると、15で割ると余りが4。これは肢②にあります。よって、正解は肢②です。にほんブログ村











