「言ひおほせて何かある」は、去来抄に出てくる、松尾芭蕉のことばで、基角（榎本基角？）の詠んだ糸桜の句は良くないと芭蕉が批評したときに、去来（向井去来？）が、咲き誇る桜の様子をよく表せているではないかと反論し、それに対して芭蕉先生が、全部言い尽くしてしまうのは駄作だと戒めたとかいう話だったと思います。 さて、平成22年の警視庁から。 10冊の書籍があり、日本語4冊、英語4冊、中国語2冊で、ハードカバーが4冊、ソフトカバーが6冊である。また、表紙が赤いものが2冊、青が3冊、白が5冊である。 これらの書籍について次のア～ウのことが分かっているとき、確実にいえるものはどれか。ア 表紙が赤い2冊の本は日本語と中国語で、そのうち1冊がハードカバーである。 イ ソフトカバーの本は、日本語、中国語それぞれ2冊あり、日本語の本はどれも表紙が白い。 ウ 英語の本のうち3冊は表紙が青く、特にハードカバーの本はどれも青い表紙である。 ①日本語のハードカバーで表紙の白い本は1冊である。 ②英語のハードカバーで表紙の青い本は1冊である。 ③中国語のソフトカバーで表紙の白い本は2冊である。 ④ハードカバーで表紙の白い本は2冊である。 ⑤ソフトカバーで表紙の青い本は2冊である。
ハードカバーは□、ソフトカバーは○とすると、この10冊の内訳は、
とりあえず、中国語の2冊は2冊ともソフトカバーです。そして、赤2冊の内訳を見ると、日本語1冊と中国語1冊ですが、中国語はソフトカバーしかないので、日本語の方がハードカバーで、
この次が急所ですよ～。実は、ソフトカバー4冊とハードカバー6冊の内訳は、全て教えてくれているのです。まさに、「いい仰せて何かある」です。
ソフトカバーは、日本語2冊で中国語2冊で英語2冊と、全部言い尽くしてしまうより、日本語2冊、中国語2冊とだけ言えば、自動的に英語は2冊となるのだから、わざわざ英語が2冊と言うのは言い過ぎですよ。そうすると、ハードカバーの方も、自動的に日本語2冊と英語2冊と決まるのだから、ハードカバーのことは何も言わなくても構わない。全ての無駄をそぎ落とした、ナイスな表現方法だったのですね。（問題を解く人にとっては大迷惑）ということで、一気にここまで進みます。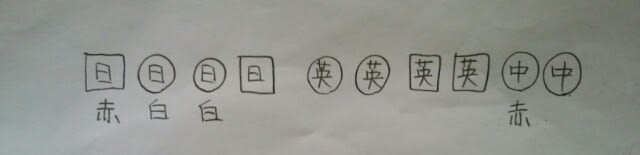
後は、英語のうちハードカバーは青だから、
英語のうち3冊が青だから、
（ハードカバーは青と言っているだけで、青がハードカバーとは言っていないことに注意）残りは全部白で、完成です。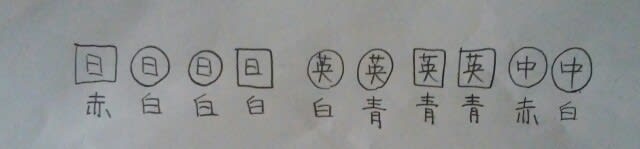
正解は、肢①です。ここをポチッとお願いします。→
にほんブログ村
ハードカバーは□、ソフトカバーは○とすると、この10冊の内訳は、とりあえず、中国語の2冊は2冊ともソフトカバーです。そして、赤2冊の内訳を見ると、日本語1冊と中国語1冊ですが、中国語はソフトカバーしかないので、日本語の方がハードカバーで、この次が急所ですよ～。実は、ソフトカバー4冊とハードカバー6冊の内訳は、全て教えてくれているのです。まさに、「いい仰せて何かある」です。ソフトカバーは、日本語2冊で中国語2冊で英語2冊と、全部言い尽くしてしまうより、日本語2冊、中国語2冊とだけ言えば、自動的に英語は2冊となるのだから、わざわざ英語が2冊と言うのは言い過ぎですよ。そうすると、ハードカバーの方も、自動的に日本語2冊と英語2冊と決まるのだから、ハードカバーのことは何も言わなくても構わない。全ての無駄をそぎ落とした、ナイスな表現方法だったのですね。（問題を解く人にとっては大迷惑）ということで、一気にここまで進みます。後は、英語のうちハードカバーは青だから、英語のうち3冊が青だから、（ハードカバーは青と言っているだけで、青がハードカバーとは言っていないことに注意）残りは全部白で、完成です。正解は、肢①です。ここをポチッとお願いします。→
にほんブログ村
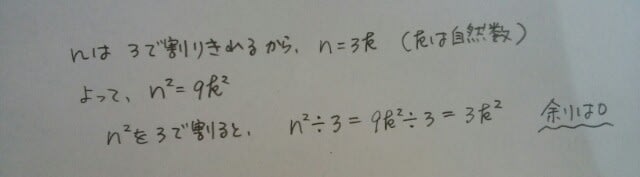ある自然数nが、グループ②の、3で割ると1余るものだったら、
グループ③だったら、
これで、全ての自然数について考えたことになります。あまりは、0か1にしかなりません。正解は、肢イです。ここをポチッとお願いします。→
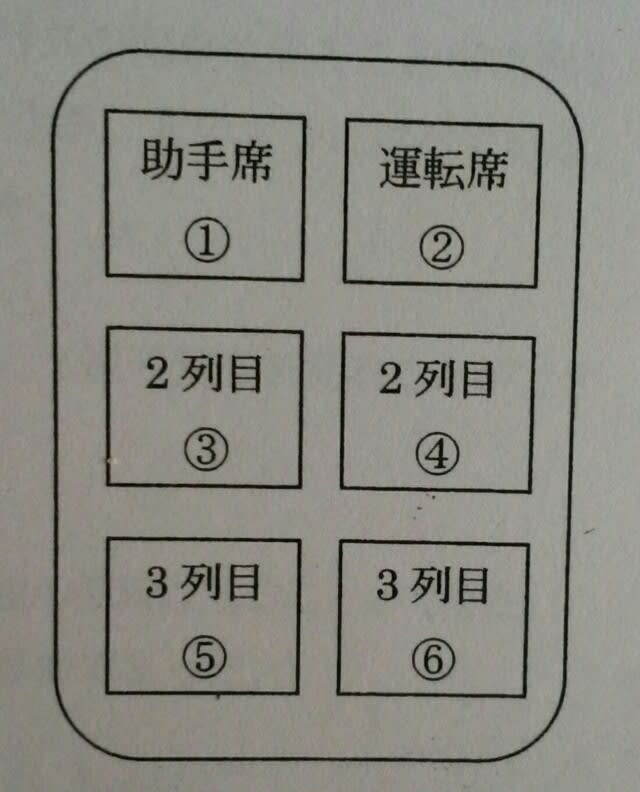・Aは1日目、2日目のどちらかで①に座った。 ・Bの2日目の座席は、②であった。 ・Cの2日目の座席は、1日目の隣の座席であった。 ・Dの2日目の座席は、1日目に座った座席の前であった。 ・Eは運転免許を持っておらず、1日目はAの隣に座った。 ・Fは2日ともCの斜め前に座った。 1 A～Fの中には2日間同じ座席に座った者がいる。 2 Aの1日目の座席は、Bの斜め前の座席であった。 3 Bの1日目の座席は、③であった。 4 Dの2日目の座席は、③であった。 5 Eの2日目の座席は、Fの真後ろの座席であった。 Aは、1日目、2日目のどちらかで①に座ったのですが、それは1日目ではなく、2日目です。
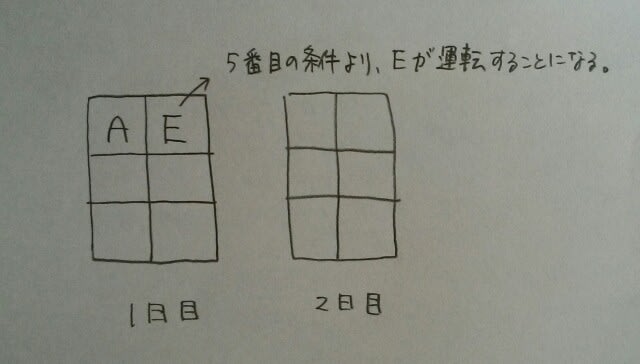よって、はじめの二つの条件より、
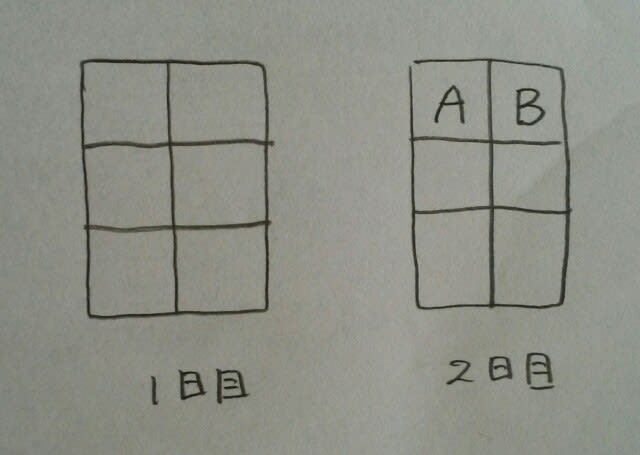次に、4つ目の条件ですが、もしもDが1日目に2列目に座っていたとしたら、2日目は1列目ですが、2日目の1列目にはAとBが座っているので、無理ですね。よって、Dは1日目は3列目、2日目は2列目。
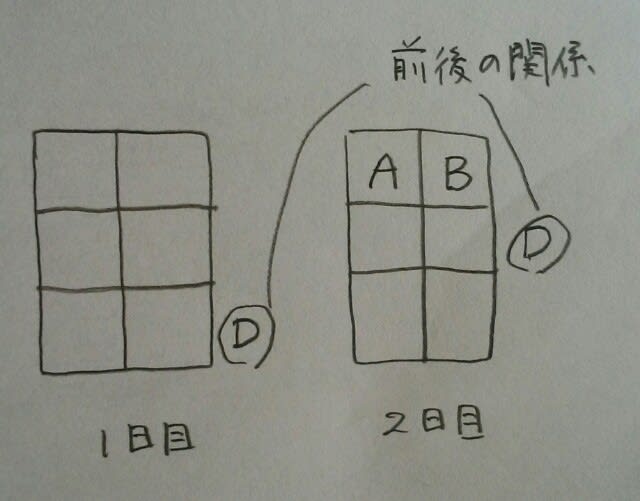なので、5番目の条件より、1日目、AとEは隣り合わせに座るのですが、2列目で隣合っちゃうと、6番目の条件が満たせません～。
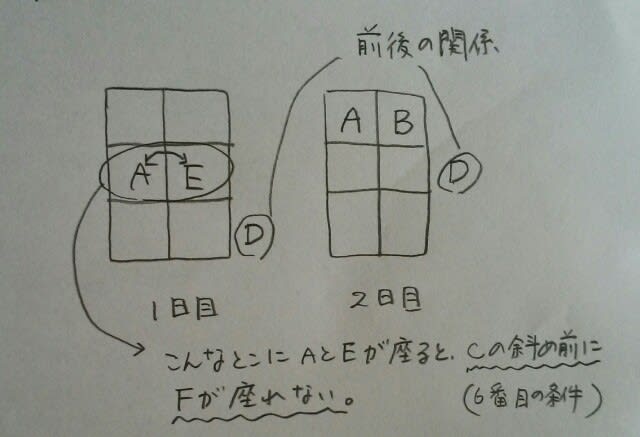CとFから、「邪魔や！お前ら、前に行け！」と怒鳴られてしまうのです。（後ろに行ったら、今度はDから文句を言われるし…やっぱり1列目に行くしかありません。）ところが、Eは私と同じく、運転免許を持っていませんので、こうなりますね。
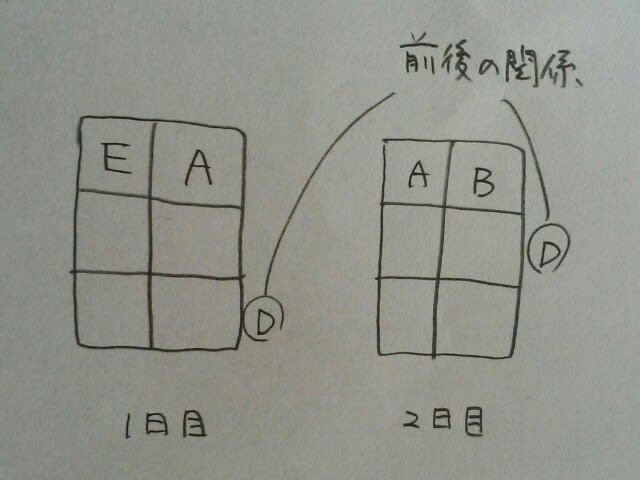そうなると、6番目の条件より、2日ともFが2列目で、Cが3列目～。
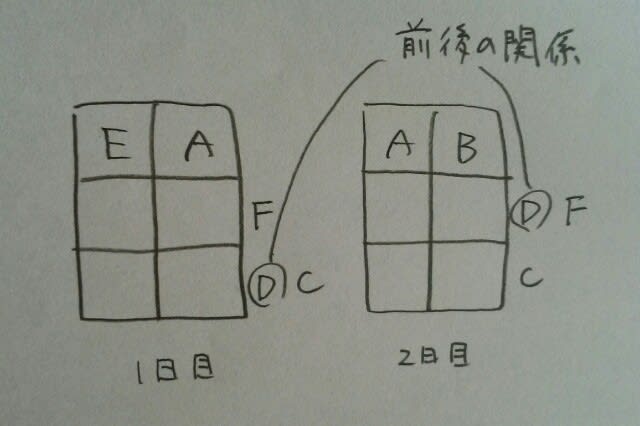残った席に残った人が入り、
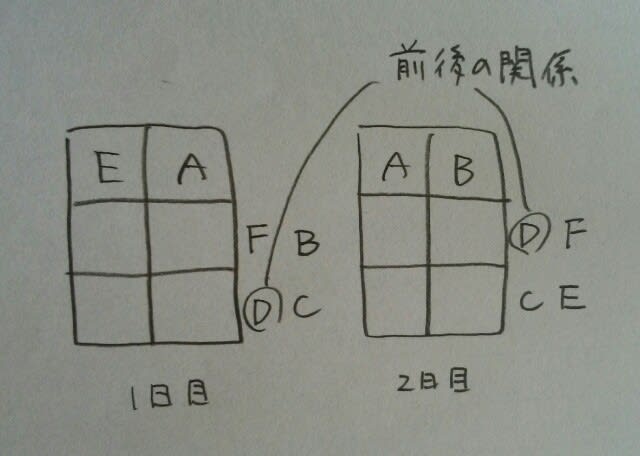Dが左か右かによって場合分けして、
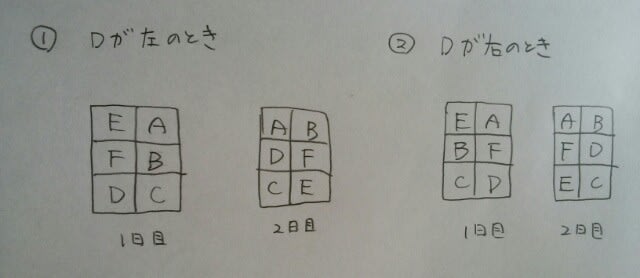肢1…2日間同じ座席に座った人はいません。肢2、肢3、肢4…あり得ますが、確実ではありません。肢5…確実ですね。正解は、肢5です。ここをポチッとお願いします。→
の計算結果が11の倍数になるように設定されている。 この方法に従って、ある書籍に書籍コードを5－00－43068－ア と付けた。この書籍を読取り機にかけると、コードの左から7番目の数字「6」を、イ と読み違えたために計算結果が227となり、11の倍数とならなかった。 このときのエラーチェック用の数字アと読取り機が読み違えた数字イの組み合わせとして正しいのはどれか。
計算結果が11の倍数になるように設定されているったって、ホントにそんな設定できるの？なぜ11の倍数になるんだろう？とか、それは野暮というものです。できるもんはできるのでしょう。まずは、
ア＝7です。次に、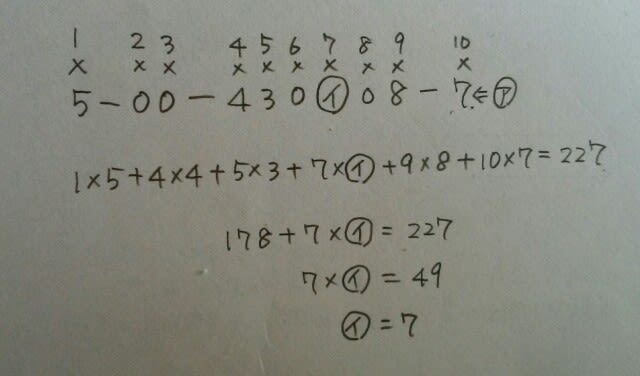
イ＝7です。よって、正解は、肢⑤です。難しそうに見えて、実は見かけ倒しですね。 手元にある本をよく見ると、あった、あった。ほら、
しかし、13桁😕。なんや、書いてあるのと違うやン！待てよ、古い本なら……あっ！
計算結果は231で、確かに11の倍数ですう。🙌ネットで調べましたら、2007年の1月から13桁に変わったそうです。この問題は平成12年、西暦2000年だから、納得納得😋。ここをポチッとお願いします→
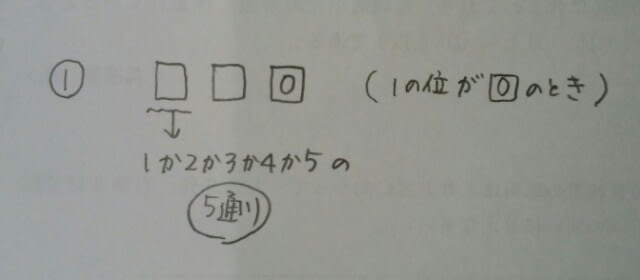仮に100の位が1だったとすると、
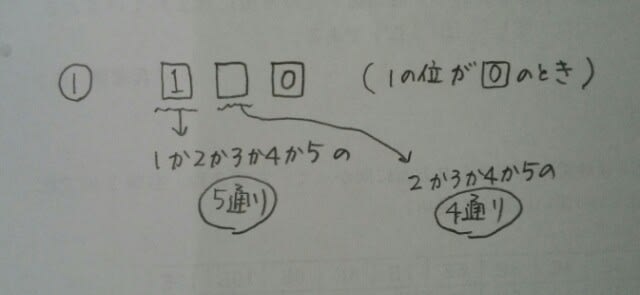よって、5×4＝20通り。
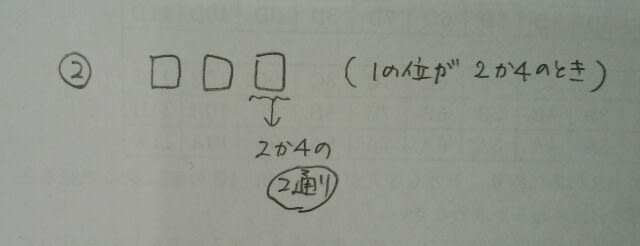仮に1の位が2だとすると、
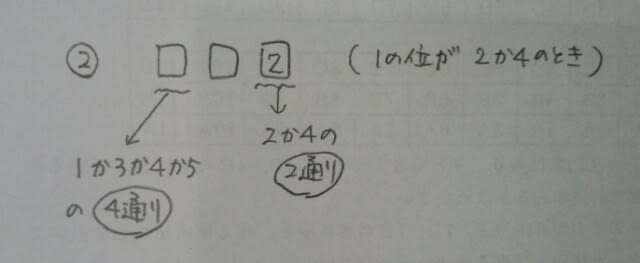仮に100の位が1だとすると、
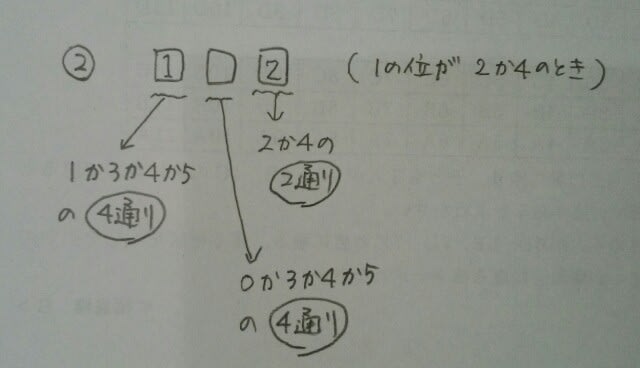という訳で、2×4×4＝32通りです。 まとめると、1の位が0の偶数が20通りあり、1の位が2か4の偶数が32通りあるので、全部で20＋32＝52通りあるので、正解は、肢③です。 えっ！場合分けしたくない？そんなワガママ言う人は、こうして下さい。 まず、奇数とか偶数とか関係なしで、とにかく3桁の整数は何通りできるでしょうか？100の位が5通り（0を入れてはいけない）、10の位が5通り（0を入れても構わない）、1の位が4通りで、5×5×4＝100通りですね。 次に、奇数は何通りあるでしょうか？奇数なら、1の位に0は入らないので、あなたの嫌いな場合分けは不要ですよ。
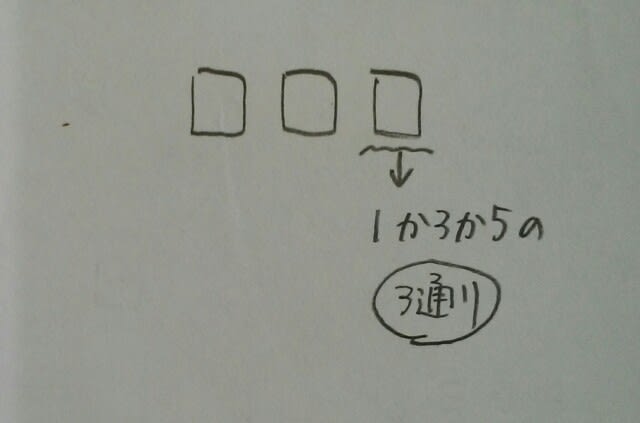仮に1の位が1だとすると、
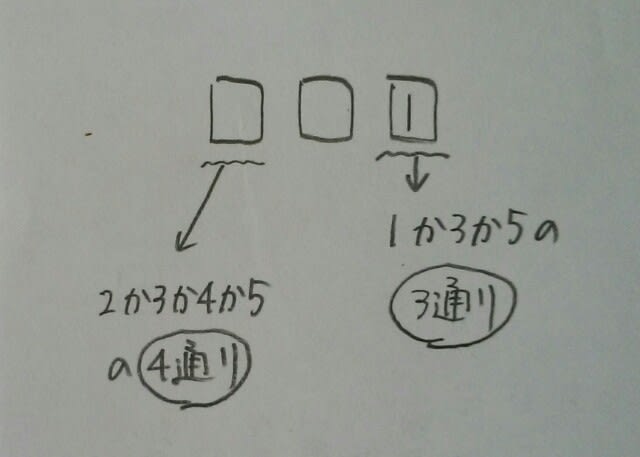仮に100の位が2だとすると、
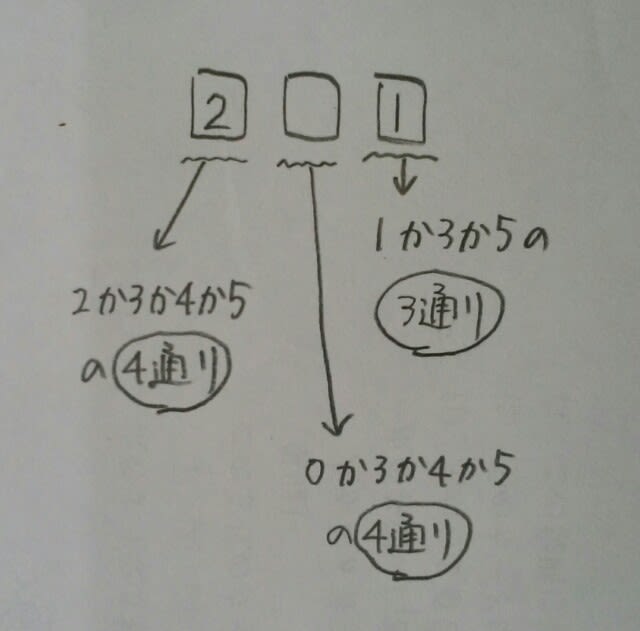よって、3×4×4＝48通り。 奇数以外はすべて偶数なので、偶数は、100－48＝52通り。ここをポチッとお願いします。→