数列6、14、22、30、38、・・・について、第30項の数と第70項の数の和として正しいのはどれか。 ①496②596③696④796⑤896 この数列は、単に、8ずつ増えていく等差数列です。等差数列の一般項は、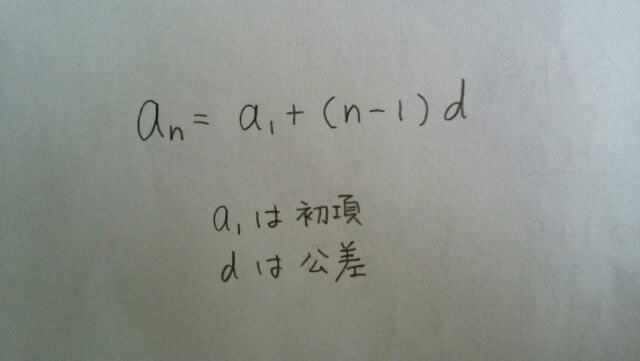 本問の場合は、初項=6、公差=8で、第30項は、nに30を代入して、
本問の場合は、初項=6、公差=8で、第30項は、nに30を代入して、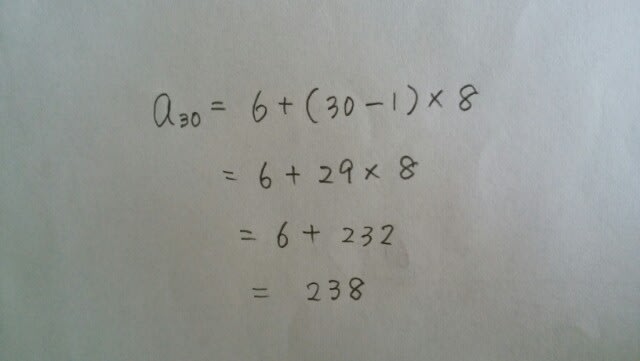 第70項は、nに70を代入して、
第70項は、nに70を代入して、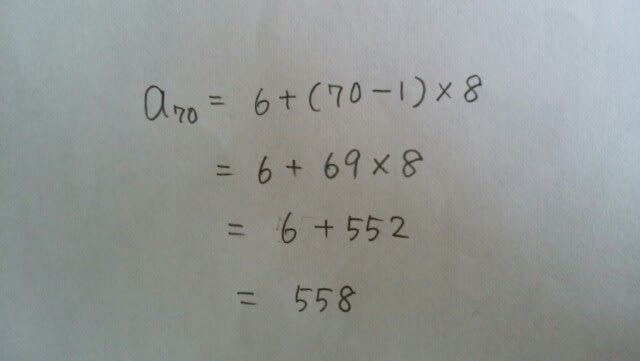 よって、その和は、238+558=796。正解は肢④です。 次に、等差数列の公式を使わずにやってみます。第1項が6、第2項が14、第3項が22、第4項が30、第5項が38。 実は、等差数列の場合は、必ず、次のような規則があるのです。第1項の「1」という数字に、公差の8を掛けると、「8」になります。そこから、2をひけば、「6」になります。第2項の「2」という数字に、公差の8を掛けると、「16」になります。そこから2を引けば「14」になります。第3項から先も、すべて同様です。だから、第30項は、30×8-2=238で、第70項は、70×8-2=558です。 (項の番号)×(公差)に、いくつかを足すか引くかをすれば、その項が分かります。ただし、これは等差数列のときだけです。
よって、その和は、238+558=796。正解は肢④です。 次に、等差数列の公式を使わずにやってみます。第1項が6、第2項が14、第3項が22、第4項が30、第5項が38。 実は、等差数列の場合は、必ず、次のような規則があるのです。第1項の「1」という数字に、公差の8を掛けると、「8」になります。そこから、2をひけば、「6」になります。第2項の「2」という数字に、公差の8を掛けると、「16」になります。そこから2を引けば「14」になります。第3項から先も、すべて同様です。だから、第30項は、30×8-2=238で、第70項は、70×8-2=558です。 (項の番号)×(公差)に、いくつかを足すか引くかをすれば、その項が分かります。ただし、これは等差数列のときだけです。

にほんブログ村
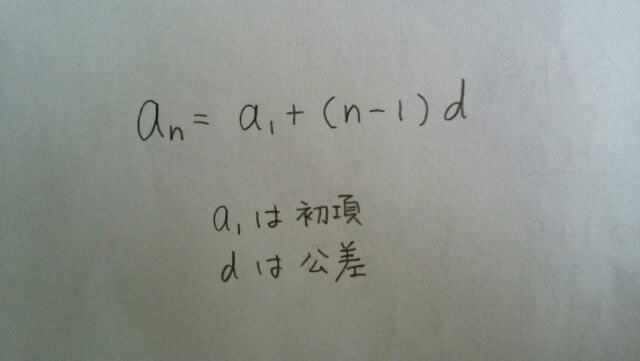 本問の場合は、初項=6、公差=8で、第30項は、nに30を代入して、
本問の場合は、初項=6、公差=8で、第30項は、nに30を代入して、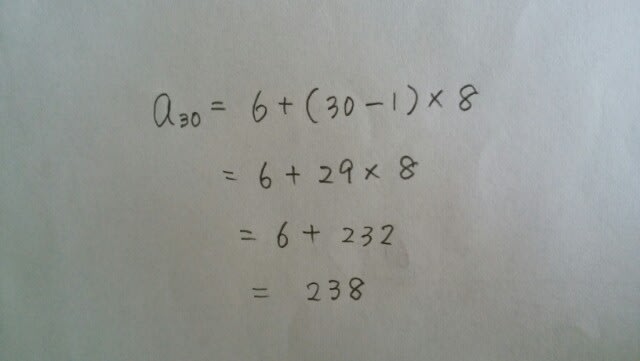 第70項は、nに70を代入して、
第70項は、nに70を代入して、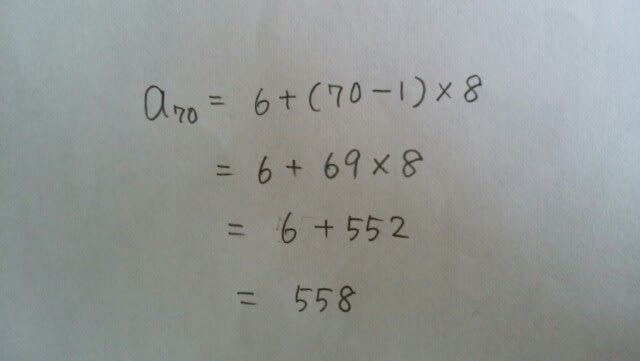 よって、その和は、238+558=796。正解は肢④です。 次に、等差数列の公式を使わずにやってみます。第1項が6、第2項が14、第3項が22、第4項が30、第5項が38。 実は、等差数列の場合は、必ず、次のような規則があるのです。第1項の「1」という数字に、公差の8を掛けると、「8」になります。そこから、2をひけば、「6」になります。第2項の「2」という数字に、公差の8を掛けると、「16」になります。そこから2を引けば「14」になります。第3項から先も、すべて同様です。だから、第30項は、30×8-2=238で、第70項は、70×8-2=558です。 (項の番号)×(公差)に、いくつかを足すか引くかをすれば、その項が分かります。ただし、これは等差数列のときだけです。
よって、その和は、238+558=796。正解は肢④です。 次に、等差数列の公式を使わずにやってみます。第1項が6、第2項が14、第3項が22、第4項が30、第5項が38。 実は、等差数列の場合は、必ず、次のような規則があるのです。第1項の「1」という数字に、公差の8を掛けると、「8」になります。そこから、2をひけば、「6」になります。第2項の「2」という数字に、公差の8を掛けると、「16」になります。そこから2を引けば「14」になります。第3項から先も、すべて同様です。だから、第30項は、30×8-2=238で、第70項は、70×8-2=558です。 (項の番号)×(公差)に、いくつかを足すか引くかをすれば、その項が分かります。ただし、これは等差数列のときだけです。
にほんブログ村










