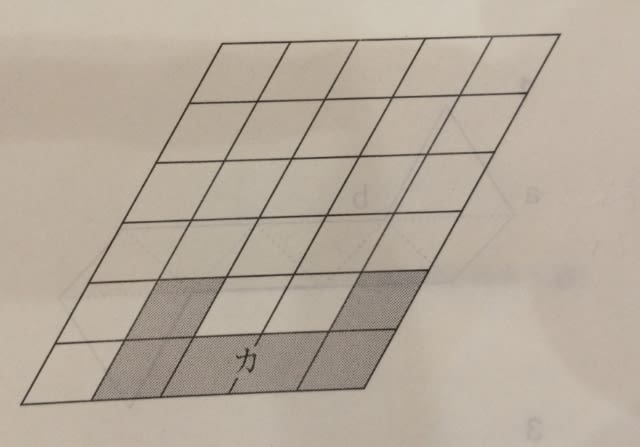
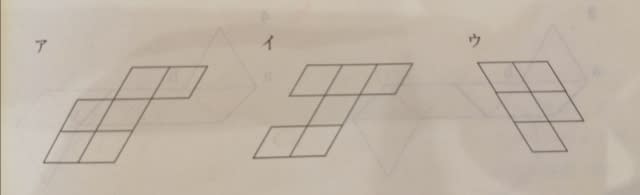
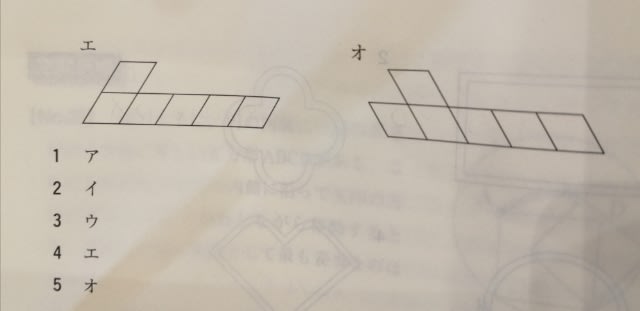
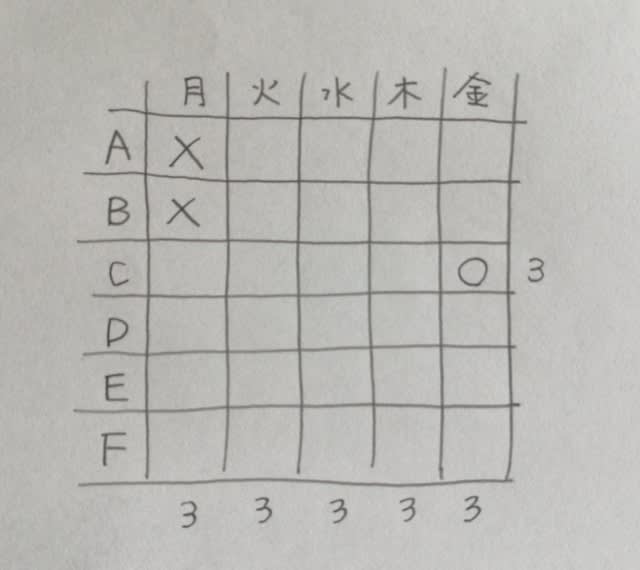
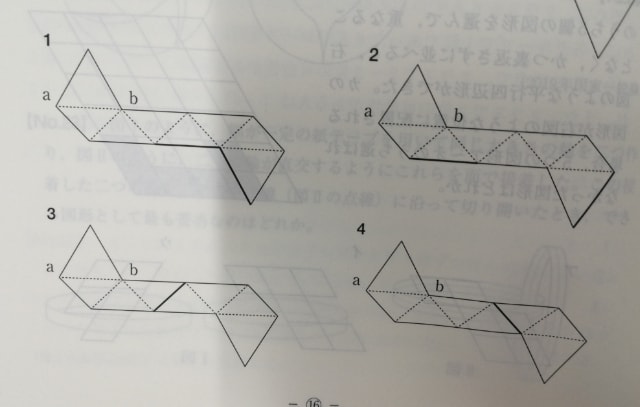
下図は、正三角形二つと直角三角形六つから成る展開図である。この展開図を点線部分で全て谷折りにして立体Xを作った。立体Xは、立方体を頂点三つを通る平面で切断し三角錐を切り落とし、さらに、別の頂点三つを通る平面で切断し三角錐を切り落としてできる立体と同じ形てある。立体Xにおいて、右図の展開図の辺abと平行な辺を全て太線で示しているのはどれか。

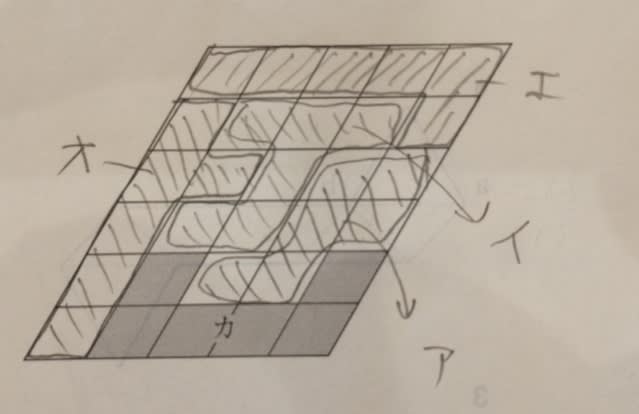
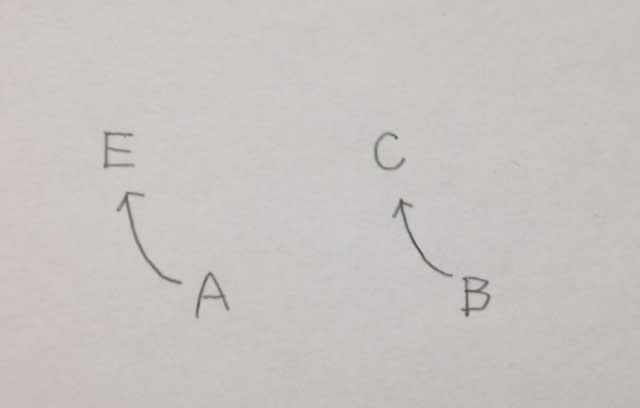
立体Xは、立方体を頂点三つ(例えば下の図のウとエとオ)を通る平面(面ウエオ)で切断し三角錐(ア−ウエオ)を切り落とし、さらに、別の頂点三つを通る平面で切断し・・・と書いてありますが、この「別の頂点三つ」がくせ者です。仮に、それを頂点ウとエとカだとすると、このようになりますね。
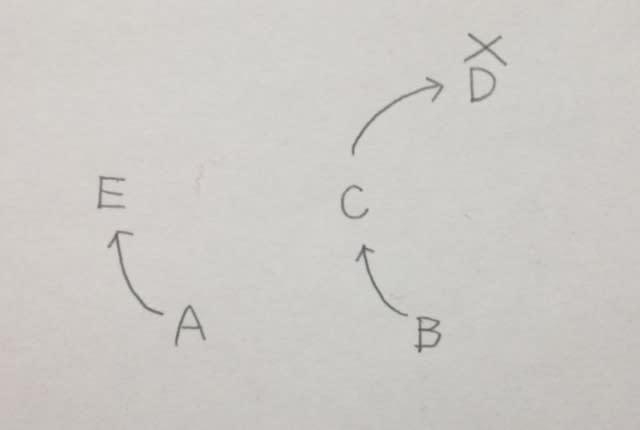
実際に切り落とすと、
このとき、展開図では、二つの正三角形が辺を共有することになります。ところが、そうはなっていません。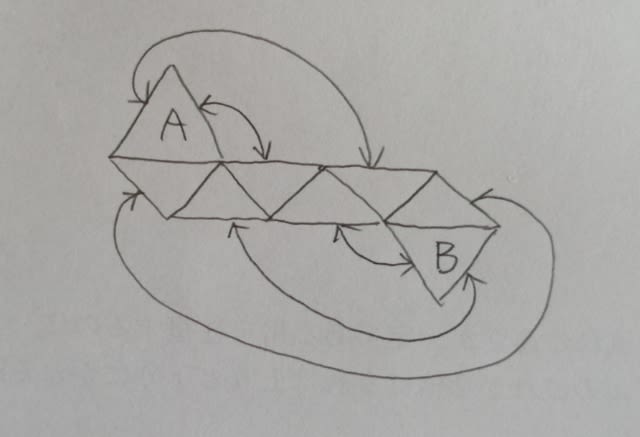
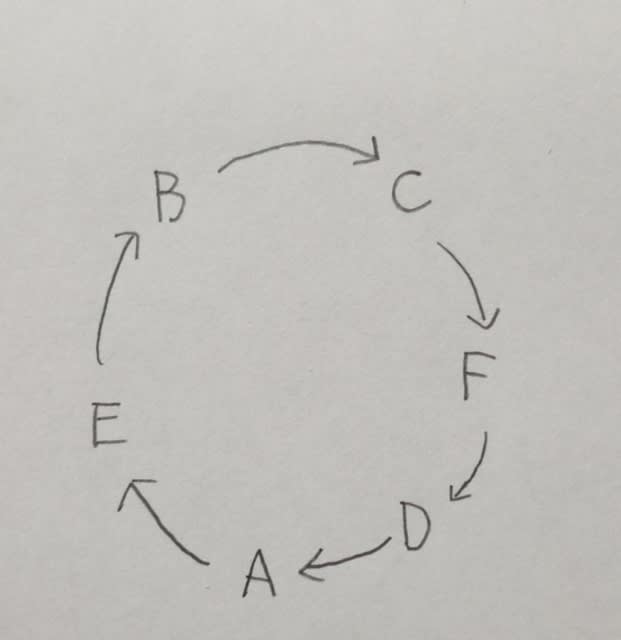
ということは、このような切断をした訳です。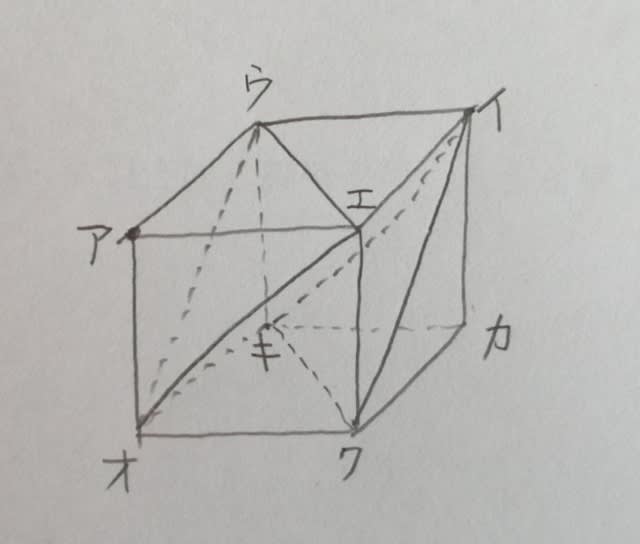
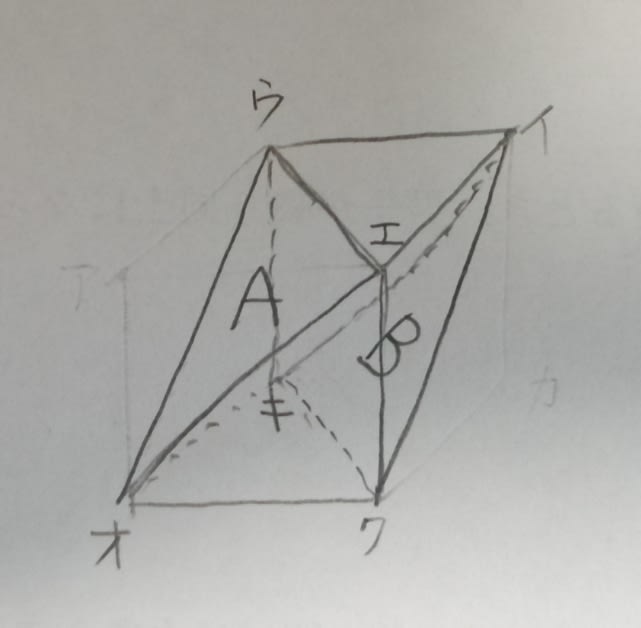
次に、展開図の辺abと平行な辺を探します。どの点をa、どの点をbにすればいいのでしょうか?展開図を見ると、正三角形の各辺は、全て直角二等辺三角形の斜辺になっています。だから、正三角形のどの辺を辺abとしても構いません。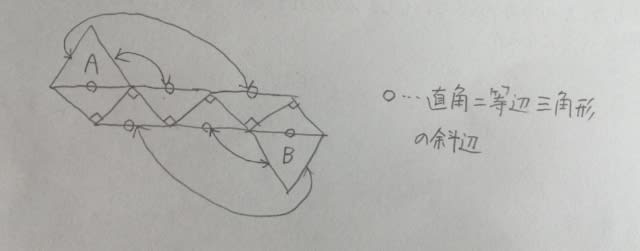
二つ上の図の辺ウエを辺abとしましょう。すると、それと平行な辺は辺キクです。辺キクは、正三角形Bの3つの辺のうち、点イを含まない辺ですね。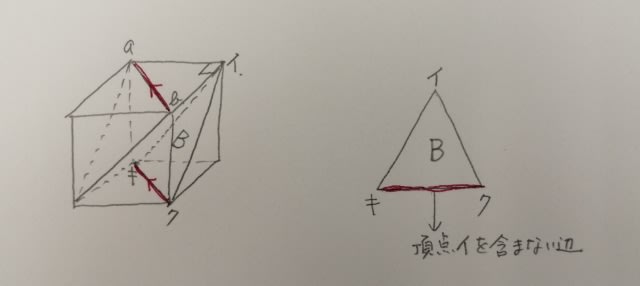

正解は、肢1です。ここをポチッとお願いします。→
にほんブログ村




立体Xは、立方体を頂点三つ(例えば下の図のウとエとオ)を通る平面(面ウエオ)で切断し三角錐(ア−ウエオ)を切り落とし、さらに、別の頂点三つを通る平面で切断し・・・と書いてありますが、この「別の頂点三つ」がくせ者です。仮に、それを頂点ウとエとカだとすると、このようになりますね。

実際に切り落とすと、

このとき、展開図では、二つの正三角形が辺を共有することになります。ところが、そうはなっていません。

ということは、このような切断をした訳です。

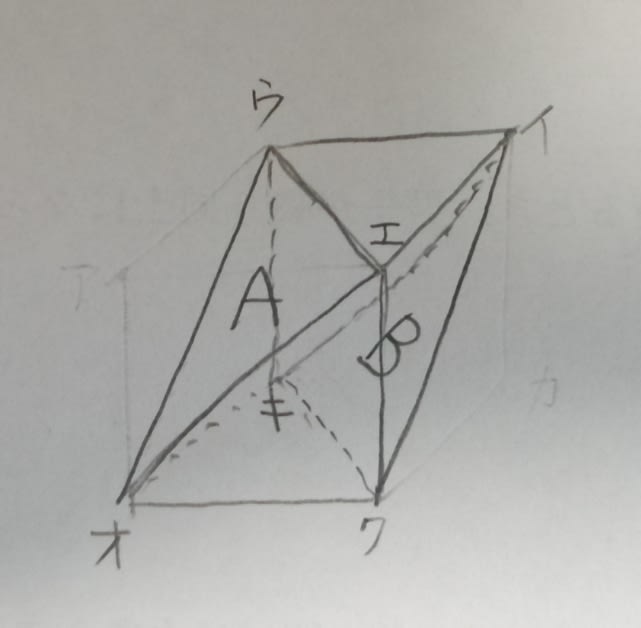
次に、展開図の辺abと平行な辺を探します。どの点をa、どの点をbにすればいいのでしょうか?展開図を見ると、正三角形の各辺は、全て直角二等辺三角形の斜辺になっています。だから、正三角形のどの辺を辺abとしても構いません。

二つ上の図の辺ウエを辺abとしましょう。すると、それと平行な辺は辺キクです。辺キクは、正三角形Bの3つの辺のうち、点イを含まない辺ですね。


正解は、肢1です。ここをポチッとお願いします。→
にほんブログ村