公務員サイトはこちら
皆さん、こんにちは。前回、
ってやつを紹介しましたが、これは、三角形の頂点のうちの1つが、原点であるときに限るということでした。今日は、三角形の頂点が3つとも原点ではないときのお話です。例えば、
この場合は、3つの頂点のうちの1つを、無理やり原点に移動させます。
嫌がっている馬を、無理やり引っ張っていく感じですかねえ。当然、3点とも座標が変わります。こんな感じです。
よって、
ゆえに、
ってな具合です。では、練習問題です。2016.7.10の、神奈川県、横浜市、川崎市、相模原市の教員採用試験からです。
ということで、
この場合は、点Cを、原点に移動させるのが楽ですねえ。
よって、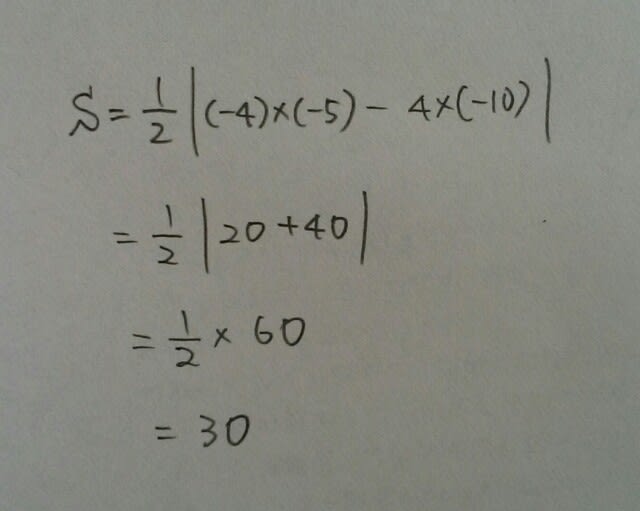
正解は、肢②です。
ここをポチッとお願いします。
http://moppy.jp/top.php?TwfKe128
毎月最大1200ptお得！【ひかりＴＶブック月額プラン】
皆さん、こんにちは。今日は、座標上での三角形の面積について説明します。まず、
だいたいの本には、こんな解説が書いてありますね。
7分の22が出てきた時点で、かなりやる気が消失するのですが、もう少し頑張って、
高校時代に、数学が得意だった人は、何が言いたいのか、もう分かっていますね！この問題は、ほぼ、暗算でできるのです。では、高校2年生にタイムスリップして、位置ベクトルで習った公式です。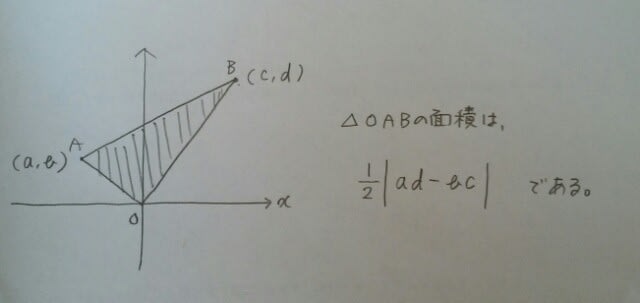
ということで、こうなるのです。
それでは、１つ練習問題です。沖縄県の教員採用試験、小学全科からです。
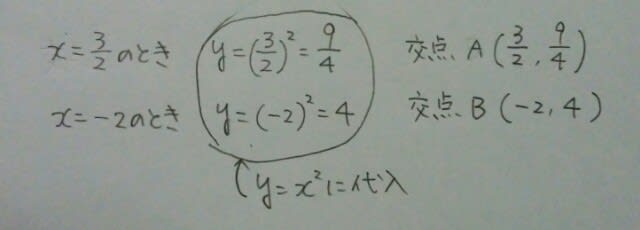慣れている人だったら、ここまでどうってことないのですが、慣れてない人は大変ですねぇ。ここからまた本に載っているようなやり方をするのはしんどいので、
正解は、肢③です。ええっ！たすき掛けの因数分解ができない？できるようにしなきゃいけないんだけど、この問題は、辛うじてクリアーできます。
便利な公式を紹介しましたが、この公式は、三角形の頂点のうちの1つが、必ず原点（0,0）でなければならないのです。頂点が3つとも原点ではないときは、どうすればよいのでしょうか？次回で説明します。ここをポチッとお願いします。
4x－4y＝3x－yのとき、次の式の値を、下の①～⑧から1つ選び、マークしなさい。
（教員採用試験、青森県） まずは、与えられた方程式を整理します。
これを、与えられた式に代入すれば終わりです。
正解は、肢⑦です。もう少し、かっこよくやってみます。分母、分子共に因数分解できますね。
よって、
さらに、答えだけ分かればいいなら、こうやっても構いません。
正解は、肢③です。
数3√5について述べた文として適切なものを、次のア～エから1つ選びなさい。 ア 3√5は、分母分子とも整数であるような分数で表すことができない。 イ 3√5は、循環する無限小数で表すことができる。 ウ 3√5は、2√10より小さい数である。 エ 3√5は、どんな有理数をかけても、結果は無理数である。 1とか、15とか、573とかは、きっちりした数なので、整数と言います。きっちりしてればよいので、－3とか、0だって整数です。ただし、整数は、3つに分類できます。①正の整数（自然数）②負の整数③0です。
小数と分数は別の者かというと、同じ者です。
全ての小数は、分数にすることができますね。では、全ての分数は、小数にすることができるでしょうか？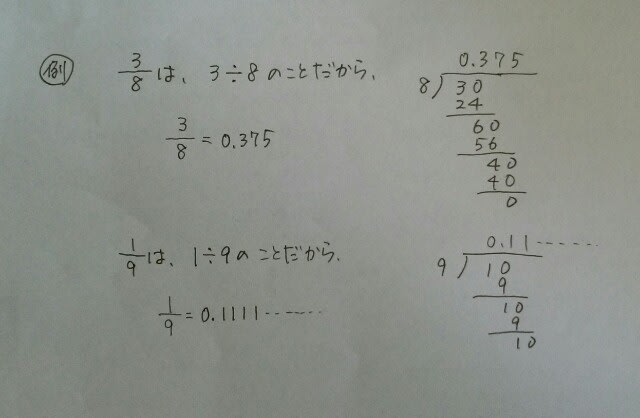
なんか、できるやつと、できないやつがありそう😩。でも、できるのです。なぜなら、どんな分数でも、それを小数に直すと、必ず循環するからです。（証明は省略）
整数、分数、小数のことを、有理数と言います。そのいずれにもあてはまらないものを、無理数と言います。代表的なものは、πと√です。ただし、√4は有理数です。なぜなら、√4は、2だからです。他にも、様々な無理数があるのですが、教養数学としては、無理数とは、πと、整数にならない√のことだなくらいで大丈夫です。 まとめます。結局、分母分子とも整数であるような分数で表すことができれば有理数、できなければ無理数です。
（注）のところですが、循環する小数は、全て、分母、分子とも整数である分数で表すことができ、その種の問題もたまに出題されています。 肢アは、言い換えると、3√5は、無理数である。となります。これは正しい。 肢イは、循環する無限小数で表すことができれば、それは分母分子ともに整数である分数になるので、有理数ということになるので、誤り。 肢ウは、
ということで誤り。 肢エは、3√5に、0という有理数を掛けると、0という有理数になるので誤り。 正解は、肢アです。
◆電話で恋するサイト
LECオンラインショップ（Ｅ学習センター）
また、線分OA上を動く点をPとし、Pを通りy軸に平行な直線とlとの交点をQとします。さらに、四角形PQRSが正方形になるように２点R、Sをとります。ただし、Sのx座標はPのx座標より小さいものとします。点Pのx座標をtとし、点Sがy軸上にあるときの、tの値として正しいものを、次の1～4の中から1つ選びなさい。
点Pのx座標がtだから、点P、Q、R、Sの座標は、次のようになります。問題に示された図は、点Sがy軸上にはありません。自分で、点Sがy軸上にあるとき、どんな正方形になるかをイメージして、図をかきます。
Pのx座標がtだから、SPの長さもt。四角形PQRSは正方形だから、PQの長さもtですね。
PQの長さがtであるという方程式を立てましょう。
この方程式を解くと、
正解は肢2です。
