2019年度国家一般職(大卒)7

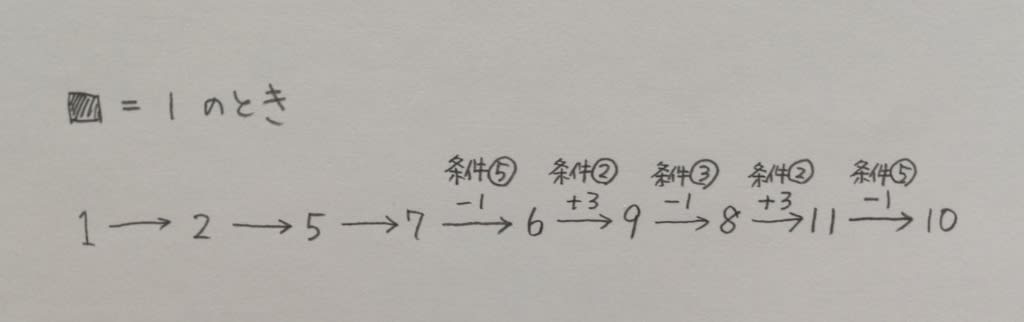
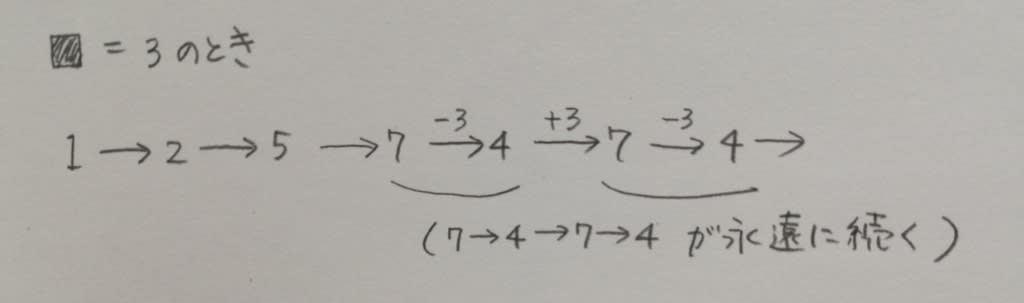A〜Eの5人が、ある週の月曜日から金曜日までの5日間のみ、書店でアルバイトを行った。A〜Eのアルバイトの日程について次のことが分かっているとき、確実にいえるのはどれか。　　　　　　　　　　　　　　　　　　　○各曜日とも2人ずつが勤務し、A〜Eはそれぞれ2日ずつ勤務した。　　　　　　　　　　　　　　　　　　　○A、B、Dは男性であり、C、Eは女性である。　　　　　　　　　　　　　　　　　　　○月曜日と火曜日に勤務したのは男性のみであった。　　　　　　　　　　　　　　　　　　　○Aが勤務した前日には必ずBが勤務していた。　　　　　　　　　　　　　　　　　　　○Aは火曜日に勤務した。また、Cは2日連続では勤務しなかった。　　　　　　　　　　　　　　　　　　　①Aは、2日連続で勤務した。　　　　　　　　　　　　　　　　　　　②Bは、火曜日に勤務した。　　　　　　　　　　　　　　　　　　　③Cは、ある曜日にAと共に勤務した。　　　　　　　　　　　　　　　　　　　④Dは、ある曜日に女性と共に勤務した。　　　　　　　　　　　　　　　　　　　⑤Eは、木曜日に勤務した。勤務表を作って、
各曜日2人ずつで、全員2日ずつ。A、B、Dが男性でC、Eが女性。Aは火曜日勤務、Cは2日連続ではない。
月曜と火曜は、男性のみなので、女性は勤務していません。また、Aの前日はB。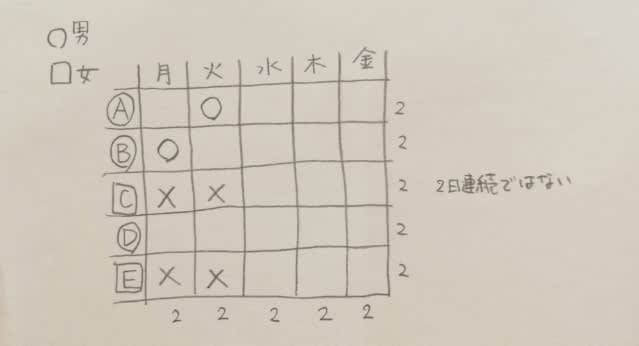
Cが水曜日に休むと、2日連続になってしまいます。金曜日に休んだとしてもやはり2日連続になってしまいます。ゆえにCは水曜日と金曜日に勤務していました。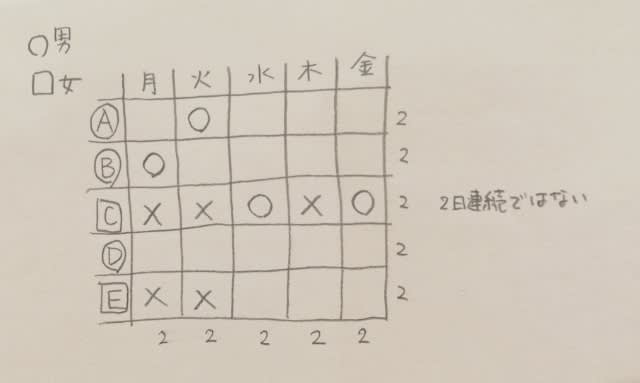
Aが月曜日に勤務すると、Bは日曜日に勤務したことになります。すると、Bは、この期間には1日だけしか勤務していないことになります。よって、Aは月曜日に勤務していませんね。月曜はBとDです。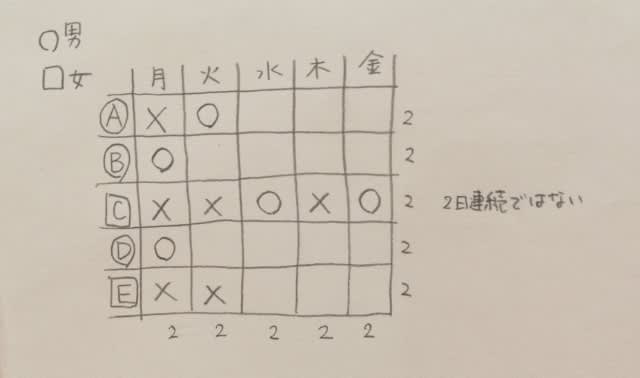
困りました。この先がよく分かりません。　　　　　　　　　　　　　　　　　　　まずは、選択肢の①を消すために、Aが木曜日に勤務していたらどうなるやろか?その際、ここに○や☓を書き込むと、後で復元ができなくなるので、同じものをもう一つ用意してから作業します。
Aが木曜日でもいけるや〜ん!選択肢①はダメや〜ん!ということが分かります。　　　　　　　　　　　　　　　　　すると、選択肢②、③、④もダメや〜ん!　　　　　　　　　　　　　　　　　　　⑤しかないや〜ん!やったや〜ん!となりまして、正解は肢⑤です。　　　　　　　　　　　　　　　　　　　念のために、Aが水曜日のときや、金曜日のときもやってみると、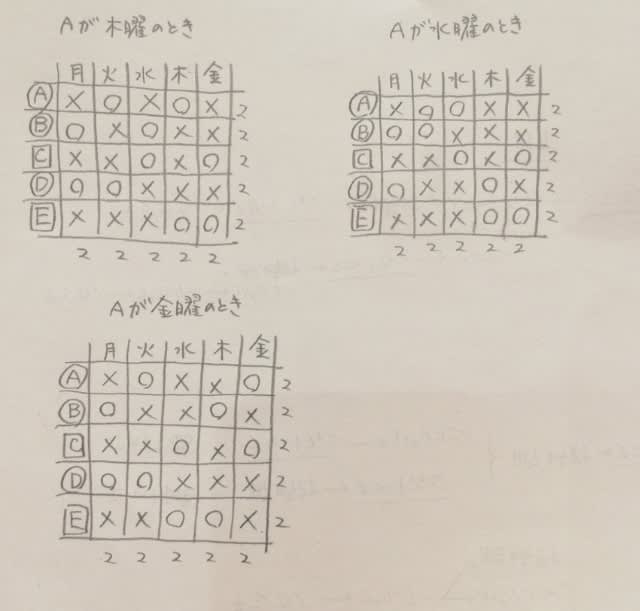
結局、3通り有り得るのですが、全部、肢⑤は当てはまっています。ここをポチッとお願いします。→
にほんブログ村

2019年度国家一般職(大卒)6

ある研究室の学生について、次のことが分かっているとき、論理的に確実にいえるのはどれか。　　　　　　　　　　　　　　　　　　　○パソコンを持っていない人は、スマートフォンを持っている。　　　　　　　　　　　　　　　　　　　○デジタルカメラを持っている人は、プリンターを持っている。　　　　　　　　　　　　　　　　　　　○プリンターを持っている人は、パソコンを持っており、かつ、腕時計を持っている。　　　　　　　　　　　　　　　　　　　○スマートフォンを持っている人は、腕時計を持っていない。　　　　　　　　　　　　　　　　　　①スマートフォンを持っている人は、デジタルカメラを持っていない。　　　　　　　　　　　　　　　　　　②デジタルカメラを持っていない人は、パソコンを持っている。　　　　　　　　　　　　　　　　　　③パソコンを持っている人は、腕時計を持っている。　　　　　　　　　　　　　　　　　　④腕時計を持っている人は、プリンターを持っている。　　　　　　　　　　　　　　　　　　⑤プリンターを持っている人は、スマートフォンを持っている。　　　　　　　　　　　　　　　　　　条件を、上から順にア、イ、ウ、エとすると、こうなります。
イとウはすぐに三段論法でつながりますし、アとエの対偶を作れば、
腕時計のところでつながりますね。
選択肢と照らし合わせると、①が確実にいえます。
ここをポチッとお願いします。→
にほんブログ村

2019年度国家一般職(大卒)5

正の整数を入力すると、次の条件①〜⑤に従って計算した結果を出力するプログラムがある。正の整数を入力してから結果が出力されるまでを1回の操作とし、1回目の操作では初期値を入力する。また、2回目以降の操作では、その前の操作で出力された結果を入力する。　　　　　　　　　　　　　　　　　　いま、条件⑤の一部が分からなくなっているが、■には、1、2、3のうちいずれかが入ることが分かっている。　　　　　　　　　　　　　　　　　　このプログラムに1を初期値として入力すると、何回目かの操作で出力された数字が10となった。このプログラムに初期値として1、2、3をそれぞれ入力したとき、それぞれの初期値に対して7回目の操作で出力される数字を合計するといくらか。　　　　　　　　　　　　　　　　　　ただし、条件に複数該当する場合は、最も番号の小さい条件だけが実行されるものとする。　　　　　　　　　　　　　　　　　　［条件］　①入力された数字が1の場合、1足す。　　　　　　　　　　　　　　　　　　　　　　　②入力された数字が2の倍数の場合、3足す。　　　　　　　　　　　　　　　　　　　　　　　③入力された数字が3の倍数の場合、1引く。　　　　　　　　　　　　　　　　　　　　　　　④入力された数字が5の倍数の場合、2足す。　　　　　　　　　　　　　　　　　　　　　　　⑤条件①〜④に該当しない場合、■引く。　　　　　　　　　　　　　　　　　　　1. 28 2. 30 3. 32 4. 34 5. 36　　　　　　　　1を初期値として入力したので、ここまでは1本道です。
7は、条件⑤にあてはまるので、■を引いた数が出力されます。でもでも、どうせ■は1か2か3ですから、全部やってみましょう。
■が1だとすると、確かに10が出力されます。
■が2だとすると、10が出力されることはありません。
■が3だとしても、10が出力されることはありません。よって、■＝1。■＝1のときの画像より、初期値が1のとき、7回目の操作で出力される数字は11。初期値が2や3のときはこうなります。
11＋10＋11＝32。正解は、肢3です。ここをポチッとお願いします。→
にほんブログ村

2019年度国家一般職(大卒)4

A、B、Cの3人が徒競走を4回行った。徒競走を1回行うごとに、1位になった人は、他の2人から1位になった人が持っているのと同じ枚数のメダルをそれぞれ受け取る約束をした。　　　　　　　　　　　　　　　　　　次のことが分かっているとき、初めにBが持っていたメダルは何枚か。　　　　　　　　　　　　　　　　　　ただし、同着はなかったものとする。また、1位になった人は常に約束どおりの枚数のメダルを受け取ったものとする。　　　　　　　　　　　　　　　　　　○1回目の徒競走では、Bが1位になった。　　　　　　　　　　　　　　　　　　○2回目と3回目の徒競走では、Aが1位になった。　　　　　　　　　　　　　　　　　　○4回目の徒競走では、Cが1位になり、AとBからそれぞれ27枚のメダルを受け取った。その結果、AとBのメダルはちょうどなくなった。　　　　　　　　　　　　　　　　　　①11枚②13枚③15枚④17枚⑤19枚　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　こんな表にしてみました。後というのは、結果という意味です。
4回目の徒競走の後、AとBは、Cに27枚ずつコインを渡しましたが、なぜ27枚ずつ渡したのでしょう？　　　　　　　　　　　　　　　　　　4回目の徒競走を行う前に、Cが27枚のメダルを持っていたからです。　　　　　　　　　　　　　　　　　　ゆえに、最後のCは27+27+27＝81枚です。
ここで、あることに気が付きます。メダルをもらった人は、もらう前の3倍の枚数になるということです。逆にいえば、メダルをもらった人は、もともとはもらった後の枚数の3分の1であったということです。
メダルを渡した人はどうなるでしょうか?こうなります。
全て、cが基準になっています。はじめの画像の表を、下から上にさかのぼっていけば、
よって、正解は、肢2です。久しぶりの更新でした。ここをポチッとお願いします。→
にほんブログ村