2019年度国家一般職(大卒)4

A、B、Cの3人が徒競走を4回行った。徒競走を1回行うごとに、1位になった人は、他の2人から1位になった人が持っているのと同じ枚数のメダルをそれぞれ受け取る約束をした。　　　　　　　　　　　　　　　　　　次のことが分かっているとき、初めにBが持っていたメダルは何枚か。　　　　　　　　　　　　　　　　　　ただし、同着はなかったものとする。また、1位になった人は常に約束どおりの枚数のメダルを受け取ったものとする。　　　　　　　　　　　　　　　　　　○1回目の徒競走では、Bが1位になった。　　　　　　　　　　　　　　　　　　○2回目と3回目の徒競走では、Aが1位になった。　　　　　　　　　　　　　　　　　　○4回目の徒競走では、Cが1位になり、AとBからそれぞれ27枚のメダルを受け取った。その結果、AとBのメダルはちょうどなくなった。　　　　　　　　　　　　　　　　　　①11枚②13枚③15枚④17枚⑤19枚　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　こんな表にしてみました。後というのは、結果という意味です。
4回目の徒競走の後、AとBは、Cに27枚ずつコインを渡しましたが、なぜ27枚ずつ渡したのでしょう？　　　　　　　　　　　　　　　　　　4回目の徒競走を行う前に、Cが27枚のメダルを持っていたからです。　　　　　　　　　　　　　　　　　　ゆえに、最後のCは27+27+27＝81枚です。
ここで、あることに気が付きます。メダルをもらった人は、もらう前の3倍の枚数になるということです。逆にいえば、メダルをもらった人は、もともとはもらった後の枚数の3分の1であったということです。
メダルを渡した人はどうなるでしょうか?こうなります。
全て、cが基準になっています。はじめの画像の表を、下から上にさかのぼっていけば、
よって、正解は、肢2です。久しぶりの更新でした。ここをポチッとお願いします。→
にほんブログ村

平成30年度警察官6

10枚のカードに1～10の数がそれぞれ1つずつ書かれている。5人が2枚ずつカードを取り、2枚の合計を得点とするとき、11点が2人、10点が2人おり、もう1人は9のカードを取った。確実に言えるのはどれか。　　　　　　　　　　　　　　　　　　　①1と9のカードを取った人がいる。　　　　　　　　　　　　　　　　　　　②2と9のカードを取った人がいる。　　　　　　　　　　　　　　　　　　　③3と8のカードを取った人がいる。　　　　　　　　　　　　　　　　　　　④4と7のカードを取った人がいる。　　　　　　　　　　　　　　　　　　　⑤5と6のカードを取った人がいる。　　　　　　　　　　　　　　　　　　　条件を整理すると、ところで、10枚のカード全ての合計は、1＋2＋3＋4＋5＋6＋7＋8＋9＋10＝55です。このうち、4人で11＋11＋10＋10＝42を取ったので、もう1人は、55－42＝13点です。そして、この13点の人は、9のカードを持っているので、もう1枚は4です。残ったカードで、10点を作るには、2＋8と3＋7しかありません。なので、あとは、11点が2人だから、正解は、肢⑤です。ここをポチッとお願いします。→
にほんブログ村

平成30年度警察官2

1～6の数のうちの一つを書いたカードが全部で12枚ある。書いてある数が同じカードは2枚ずつある。これらを6人が2枚ずつ取ったとき、次のようになった。このとき、正しく言えるのはどれか。　　　　　　　　　　　　　　　　　　　・各人の2枚のカードの数の合計はそれぞれ4、5、6、8、9、10であった。　　　　　　　　　　　　　　　　　　　・2枚が同じ数のカードになった者はいない。①1と3のカードを取った者と3と6のカードを取った者がいる。　　　　　　　　　　　　　　　　　　　②1と5のカードを取った者と3と5のカードを取った者がいる。　　　　　　　　　　　　　　　　　　　③2と3のカードを取った者と2と6のカードを取った者がいる。　　　　　　　　　　　　　　　　　　　④2と4のカードを取った者と4と6のカードを取った者がいる。　　　　　　　　　　　　　　　　　　　⑤3と5のカードを取った者と4と5のカードを取った者がいる。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　合計が4、5、6、8、9、10の人をそれぞれA、B、C、D、E、Fとすると、Aは合計が4なので、1＋3か2＋2ですが、2枚が同じカードの人はいなかったので、1＋3しかありません。同様にFは合計が10なので、4＋6しかありません。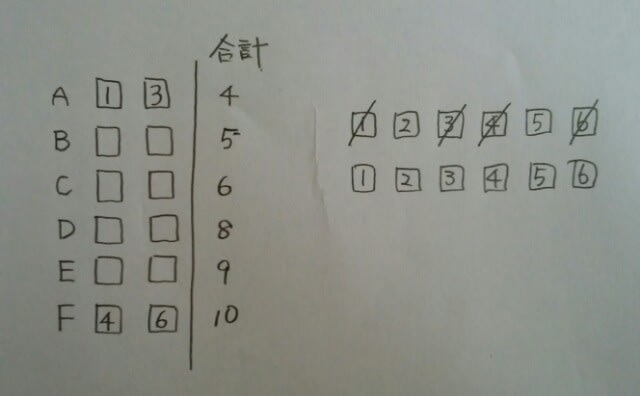Bは合計が5なので、1＋4か2＋3です。もしも1＋4だったら……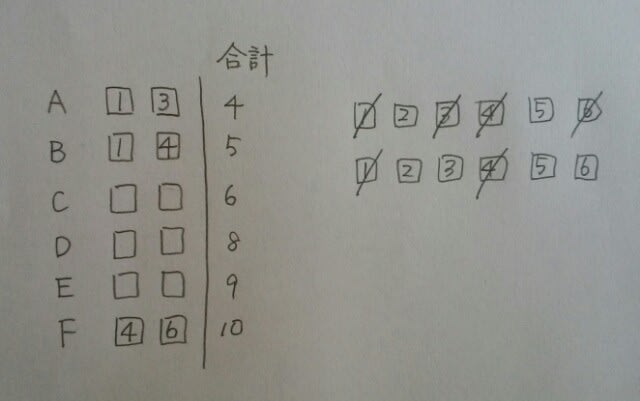Cは、もう2枚で6になりません。（1、4のカードがなくなったので、1＋5も2＋4も両方無理）よって、Bは2＋3だったのですね。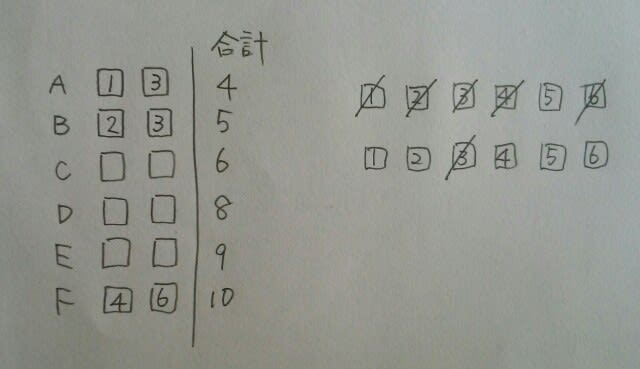Eは合計9なので、4＋5。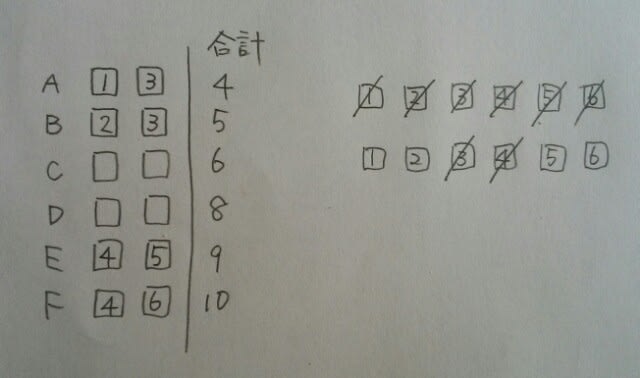Cは1＋5で、Dは2＋6。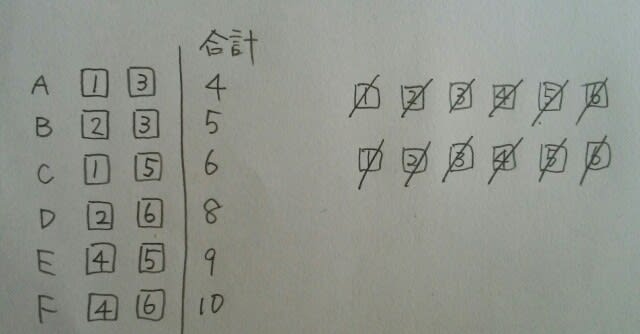正解は、肢③です。ここをポチッとお願いします。→
にほんブログ村

大阪府公立学校教員採用試験no26（2017.7.7）

次の表は、ある中学校2年1組で実施された英語と数学のテストの得点分布である。この表から、英語と数学の得点の平均値が61点以上である生徒は最大で何人と考えられるか。次の①～⑤から最も適切なものを一つ選べ。ただし、英語、数学ともに満点は100点とする。また、英語と数学の得点の平均値は小数第1位を四捨五入するものとする。①26人②27人③28人④29人⑤30人　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　英語と数学の平均値が61点以上ならば、英語と数学の合計点は、61×2＝122点以上。　　　　　　　　　　　　　　　　　　　　仮に、英語が0～20点の生徒（表を見ると2人いる）が、2人とも20点だったとすると、数学は102点以上でなければなりません。それは無理ですね。よって、英語が0～20点だった人の中には、英語と数学の平均値が61点以上の人はいません。このように考えていきますと、よって、○で囲んだところを合わせて、最大で28人。正解は、肢③です。　　　　　　　　　　　　　　　　　　　　　さて、それでは、最も少ないときは何人でしょうか？答えは、動物画像の下です。ここをポチッとお願いします。→
にほんブログ村16人。

国家一般職（高卒）no10 2017.9.3

図のように、6段から成る本棚があり、本棚の各段に、マンガ本を20冊ずつ並べることとした。本棚に並べるマンガ本は、A～Eの五つのシリーズであり、Aは1～35巻、Bは1～15巻、Cは1～20巻、Dは1～30巻、Eは1～20巻から成っていた。　　　　　　　　　　　　　　　　　　　マンガ本は、1段目の左端から並べ始め、一つの段に並べたマンガ本が20冊となったときは、その一つ下の段の左端から並べた。　　　　　　　　　　　　　　　　　　　また、同じシリーズのマンガ本は、巻数の小さいものから順に連続して並べ、一つのシリーズのマンガ本を全て並べ終わったときには、その続きから、別のシリーズのマンガ本を同様に並べた。　　　　　　　　　　　　　　　　　　　マンガ本を全て並べ終わったときの状況について、次のことが分かっているとき、確実にいえるのはどれか。　　　　　　　　　　　　　　　　　　　○1段目には二つのシリーズのマンガ本が並んでいた。　　　　　　　　　　　　　　　　　　　○2段目の右端のマンガ本の巻数は5であった。　　　　　　　　　　　　　　　　　　　○3、5、6段目にはそれぞれ一つのシリーズのマンガ本が並んでいた。　　　　　　　　　　　　　　　　　　　○5段目の左端のマンガ本の巻数は16であった。　　　　　　　　　　　　　　　　　　　①Aは4段目と5段目に並んでいた。　　　　　　　　　　　　　　　　　　　②Bは4段目に並んでいた。　　　　　　　　　　　　　　　　　　　③Cは3段目に並んでいた。　　　　　　　　　　　　　　　　　　　④Dは1段目と2段目に並んでいた。　　　　　　　　　　　　　　　　　　　⑤Eは6段目に並んでいた。　　　　　　　　　　　　　　　　　　　条件を整理すると、5段目の左端が16巻だということは、4段目の右端は15巻。ゆえに、このシリーズは、4段目の左から6冊目から始まっています。そして、5段目は一つのシリーズなので、4段目から5段目にかけて、同じシリーズのマンガ本最低35冊が並んでいます。ところが、35冊以上あるのはAのみなので、Aは、4段目と5段目に並んでおり、肢①が正解です。もうちょっとやってみると、1段目は二つのシリーズなので、Bから始まるしかありません。1段目から2段目にかけては、20冊あるCかEです。6段目は一つのシリーズだから、20冊のCかE。2段目から4段目にかけては、残ったD（30冊）ですね。CとEは入れかえ可。ここをポチッとお願いします。→
にほんブログ村