細見静香さんに会ってみたら、
だったり、大岩田豪毅さんに会ってみたら、
だったり、名前と実態がかけ離れている場合がたまにあります。 平成29年警察官（大卒）より。 1辺の長さが1cmの正三角形を、図のように1段目は1個、2段目は3個、3段目は5個というように、全部で256個を連結させて一つの大きな正三角形を描いた。このとき大きな正三角形の底辺の長さはいくらか。
①11cm ②12cm ③13cm ④15cm ⑤16cm 1段作ると、小さな正三角形は1個しか使いません。2段作ると、小さな正三角形は、1＋3＝4個使います。3段作ると、小さな正三角形は、1＋3＋5＝9個使いますので、
ということになり、256個の正三角形を使ったということは、256＝16＋16だから、
1段のとき、底辺の長さは1cm、2段のとき、底辺の長さは2cm、3段のとき、底辺の長さは3cmですから、16段のとき、底辺の長さは16cm。正解は、肢⑤です。 ところで、三角数、四角数について知っていますね。1＋2＋3＋……………＋n＝1/2×n（n＋1）が三角数。 1＋3＋5＋……………＋（2n－1）＝nの2乗が四角数。
なぜそんな名前かというと、
すると、本問の図は三角形、なのに四角数？という変な疑問が生じてくるのです。勿論、
こうやりゃ四角数でしょ！と言われれば、そうなんだけど。やはり、名前に囚われるといけませんねえ。 なんか、三角数とか四角数とか知らなかった方がスッキリ答えが出せたような一問でした。 ここをポチッとお願いします。→
にほんブログ村
だったり、大岩田豪毅さんに会ってみたら、だったり、名前と実態がかけ離れている場合がたまにあります。 平成29年警察官（大卒）より。 1辺の長さが1cmの正三角形を、図のように1段目は1個、2段目は3個、3段目は5個というように、全部で256個を連結させて一つの大きな正三角形を描いた。このとき大きな正三角形の底辺の長さはいくらか。①11cm ②12cm ③13cm ④15cm ⑤16cm 1段作ると、小さな正三角形は1個しか使いません。2段作ると、小さな正三角形は、1＋3＝4個使います。3段作ると、小さな正三角形は、1＋3＋5＝9個使いますので、ということになり、256個の正三角形を使ったということは、256＝16＋16だから、1段のとき、底辺の長さは1cm、2段のとき、底辺の長さは2cm、3段のとき、底辺の長さは3cmですから、16段のとき、底辺の長さは16cm。正解は、肢⑤です。 ところで、三角数、四角数について知っていますね。1＋2＋3＋……………＋n＝1/2×n（n＋1）が三角数。 1＋3＋5＋……………＋（2n－1）＝nの2乗が四角数。なぜそんな名前かというと、すると、本問の図は三角形、なのに四角数？という変な疑問が生じてくるのです。勿論、こうやりゃ四角数でしょ！と言われれば、そうなんだけど。やはり、名前に囚われるといけませんねえ。 なんか、三角数とか四角数とか知らなかった方がスッキリ答えが出せたような一問でした。 ここをポチッとお願いします。→
にほんブログ村
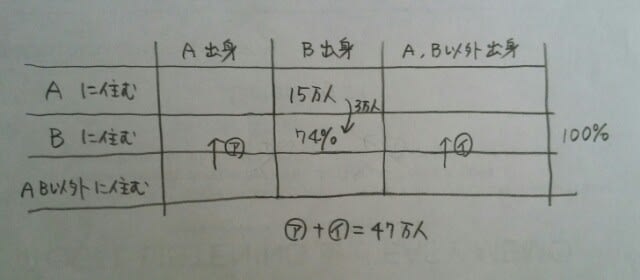Bは大人気で、たったの1年で、3＋47＝50万人も人口が増加（一人も生まれず、一人も死ななければ）。昨年度のBの総人口をxとするのがよさそうですね。
今年度のBの総人口は、x＋50（万人）であり、そのうちの70％がB出身なので、0.7（x＋50）＝0.74x＋3。これを解くと、x＝800（万人）です。 また、Aは、減少した3万人が100－95＝5％に当たるので、昨年度は3×20＝60万人でした。 よって、今年度のAは60－3＝57万人。今年度のBは800＋50＝850万人。その差は850－57＝793万人で、正解は、肢5です。 それにしてもねえ。800万人もいて、一人も生まれず、一人も死なない都市なんて……。😵こんな統計調査など要らん！という人はここをポチッとお願いします。→
前回の記事の途中まで再掲します。平成17年の地方上級からです。 表に1～5の数が一つずつ書かれた5枚のカードが裏返しに置かれている。A～Cの3人がこの中から1枚ずつカードを抜き取り、手に持ったカードの表を前に向けて立った。このとき、3人はいずれも他の2人のカードは見えるが、自分のカードは見えない。3人は、自分が他の2人のカードの数よりも大きい数のカードを持っていると分かったときには「勝った」、自分のカードの数より大きい数のカードを持っている者がいると分かったときには「負けた」、どちらとも判断できないときには「分からない」と言うことにした。 3人がA、B、Cの順にそれぞれ、見えているカードとそれまでに他の者の発言があるときはその発言とから、次のように述べた。このとき、各人の持っているカードについて確実にいえるのはどれか。 A 「分からない。」 B 「分からない。」 C 「負けた。」 ①Aは4を持っている。 ②Aは5を持っている。 ③Bは4を持っている。 ④Cは1を持っている。 ⑤Cは2を持っている。 Aは、どんなときに「勝った。」と発言するでしょうか？BとCが、1と2（順不同）を持っていたときですね。（自分は必ず3以上の数を持っていることになる） 次に、Aは、どんなときに「負けた。」と発言するでしょうか？BかCが5を持っていたときですね。（自分は4以下だから） Aは、「分からない。」と発言したのだから、こういうことです。
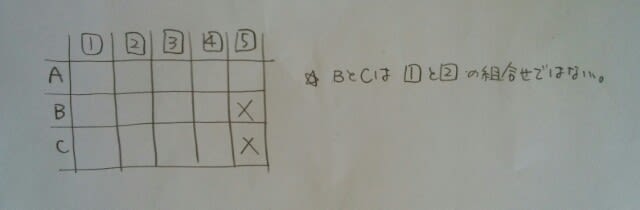
ここで、大事なことがあります。 BもCも、Aの発言を聞いていたということです。 先ほどの表は、問題を解いている我々だけが知っていることではなく、A、B、C3人とも知っているということなのです。例えば、BもCも、自分は5のカードを持っていないと気が付いているのです。 Bは、どんなときに「勝った。」と発言するでしょうか？AとCが1と2（順不同）を持っていたときですね。 どんなときに「負けた。」と発言するでしょうか？AかCが4以上のカードを持っていたときですね。（自分は4以下だと知っているから） Bは、「分からない。」と発言したのだから、こうです。
次に発言するCは、この表のような状態であることに気が付いていますよ。Cはこう考えます。 「俺はどうせ3以下の小せえやつさ。もしもAかBが3以上のカードを持っていたら俺の負け😩。AとBが1と2（順不同）なら俺の勝ち🙌。さあ、勝負だ！」と、AとBのカードを見てみますと、「おっと、いけねえ！負けちまった～😵」ということで、AかB（または2人とも）は3か4を持っていました。ところが、Bが3を持っていたなら、
ということになり、AとCが1と2を持っていることになり、△に違反します。 ここまでは、間違ってはいませんので、ここから先を訂正します。Aが3を持っていたらどうなるでしょうか？
Bは、AとCのカードを見て、こう考えます。（例えば、Aが3で、Cが1）
「ん？Cの野郎、1だな。ほんとに小せえ奴だ。俺とCは1と2の組み合わせじゃあねえから、俺は1でも2でも3でもねえ。4だ。はっはっは。俺の勝ちじゃねえか。お～い、僕、勝ちましたよ～🙌」 Aが3でCが2だったとしても同じことですね。つまり、もしもAが3だったら、Bは「勝った。」と発言するのです。よって、Aは3ではありません。なので、Bは4です。（Cは、AとBのカードの中に、3か4があったから、「負けた。」と発言したのですから）
Aは1か2で、AとCは1と2の組み合わせではないので、Cは3です。
正解は変わらず、肢③です。まあ、許してやるよって方は、ここをポチッとお願いします。→
この記事には、間違いが含まれています。訂正記事（おっといけねえ！間違っちまった！②）で、始めからの解説があります。平成17年の地方上級からです。 表に1～5の数が一つずつ書かれた5枚のカードが裏返しに置かれている。A～Cの3人がこの中から1枚ずつカードを抜き取り、手に持ったカードの表を前に向けて立った。このとき、3人はいずれも他の2人のカードは見えるが、自分のカードは見えない。3人は、自分が他の2人のカードの数よりも大きい数のカードを持っていると分かったときには「勝った」、自分のカードの数より大きい数のカードを持っている者がいると分かったときには「負けた」、どちらとも判断できないときには「分からない」と言うことにした。 3人がA、B、Cの順にそれぞれ、見えているカードとそれまでに他の者の発言があるときはその発言とから、次のように述べた。このとき、各人の持っているカードについて確実にいえるのはどれか。 A 「分からない。」 B 「分からない。」 C 「負けた。」 ①Aは3を持っている。 ②Aは5を持っている。 ③Bは4を持っている。 ④Cは1を持っている。 ⑤Cは2を持っている。 Aは、どんなときに「勝った。」と発言するでしょうか？BとCが、1と2（順不同）を持っていたときですね。（自分は必ず3以上の数を持っていることになる） 次に、Aは、どんなときに「負けた。」と発言するでしょうか？BかCが5を持っていたときですね。（自分は4以下だから） Aは、「分からない。」と発言したのだから、こういうことです。
ここで、大事なことがあります。 BもCも、Aの発言を聞いていたということです。 先ほどの表は、問題を解いている我々だけが知っていることではなく、A、B、C3人とも知っているということなのです。例えば、BもCも、自分は5のカードを持っていないと気が付いているのです。 Bは、どんなときに「勝った。」と発言するでしょうか？AとCが1と2（順不同）を持っていたときですね。 どんなときに「負けた。」と発言するでしょうか？AかCが4以上のカードを持っていたときですね。（自分は4以下だと知っているから） Bは、「分からない。」と発言したのだから、こうです。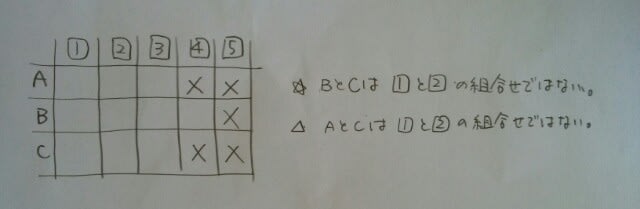
次に発言するCは、この表のような状態であることに気が付いていますよ。Cはこう考えます。 「俺はどうせ3以下の小せえやつさ。もしもAかBが3以上のカードを持っていたら俺の負け😩。AとBが1と2（順不同）なら俺の勝ち🙌。さあ、勝負だ！」と、AとBのカードを見てみますと、「おっと、いけねえ！負けちまった～😵」ということで、AかB（または2人とも）は3か4を持っていました。ところが、Bが3を持っていたなら、
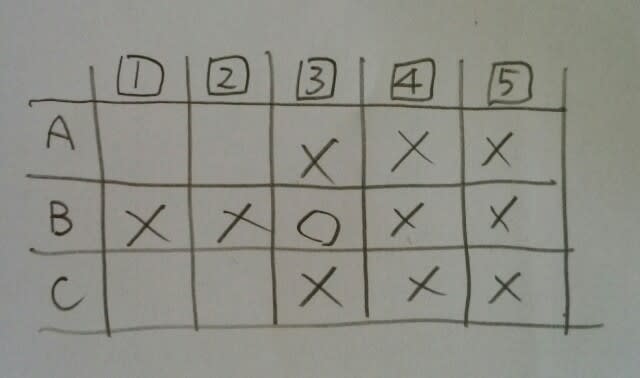ということになり、AとCが1と2を持っていることになり、△に違反します。 また、Cは負けたのだから、ほんとに小せえ奴で、1か2しか持っていません。すると、やはり△の条件から、Aは1でも2なく、3を持っていました。
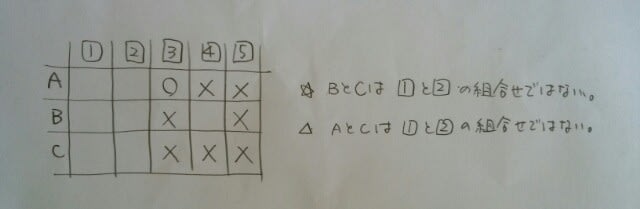さらに、もしもBが1か2なら、☆の条件に違反するので、Bは4を持っていました。Cは1か2か不明です。正解は、肢③です。
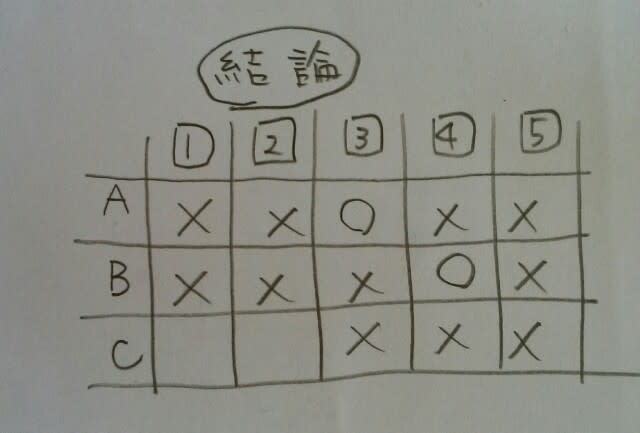ここをポチッとお願いします。→